Derivadas de Funciones Logarítmicas

Derivadas Logarítmicas

A pesar de que las derivadas logarítmicas muchas veces está relacionada con las derivadas exponenciales es importante saber diferenciar los tipos de derivadas y no confundirlas. Para ello es necesario definir el concepto y definición de un logaritmo.

El logaritmo de un número n es el exponente al que debe elevarse la base para obtener dicho número n

Contenidos

Tipos de Logaritmos
1. Logaritmos en base 10:
2. Logaritmos naturales:
Propiedades de los Logaritmos
Fórmulas de derivadas de logaritmos
Derivadas Logarítmicas Resueltas

Tipos de Logaritmos

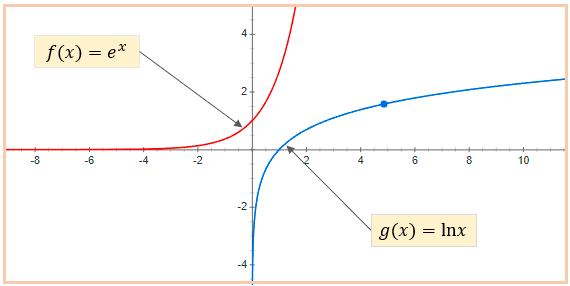
Los logaritmos pueden estar en diferentes valores de base, sin embargo los matemáticos solamente han elegido dos tipos, los logaritmos en base 10 y los logaritmos naturales , vamos a definir brevemente cada uno de los logaritmos para entenderlo mejor, pero antes vamos a observar la gráfica de la función e^x y la función ln x, dichas funciones son crecientes y continuas en sus respectivos dominios, tal como se ilustra en la imagen.

Gráfica de la Función exponencial y logarítmica

Logaritmos en base 10:

Los logaritmos en base 10 son logaritmos también llamados logaritmos vulgares o logaritmos decimales, están representados por el símbolo log y por lo general no se le coloca la base, pues se entiende que está en base diez (10).

Logaritmos naturales:

Estos logaritmos están representados simbólicamente como ln y su base es el número e cuyo valor irracional es de 2.718281828...

Propiedades de los Logaritmos

Sin importar el valor de las bases, los logaritmos tienen las mismas propiedades y nos servirán de mucha ayuda ya sea que estemos resolviendo ecuaciones logarítmicas, derivadas o integrales.

1. $\displaystyle \log A+\log B=\log AB$

2. $\displaystyle \log A-\log B=\log \frac{A}{B}$

3. $\displaystyle A\log B=\log {{B}^{A}}$

Fórmulas de derivadas de logaritmos

Ahora veamos las fórmulas que estaremos utilizando en este post, las que nos servirán para las derivadas logarítmicas

$\displaystyle \frac{d}{dx}\ln u=\frac{\frac{du}{dx}}{u}$

Nota: Recordar el u es el argumento de la función logarítmica.

Derivadas Logarítmicas Resueltas

Ejemplo 1. Resuelva la siguiente derivada

$\displaystyle y=\ln 5x$

Solución:

En este primer ejemplo, observamos que nuestro argumento es 5x, es decir que u = 5x, si aplicamos la fórmula de la derivada de un logaritmo natural. Entonces tenemos:

$\displaystyle y'=\frac{\frac{d}{dx}\left( 5x \right)}{5x}$

Como resultado de la derivada en la parte del numerador, tenemos.

$\displaystyle y'=\frac{5}{5x}$

Simplificando . . .

Resultado:

$\displaystyle y'=\frac{1}{x}$

Ejemplo 2. Resuelva la siguiente derivada

$\displaystyle y=\ln \left( 8x+3 \right)$

Solución:

En este ejemplo el argumento ahora pasa estar dentro del paréntesis, es decir u = 8x +3, por lo que aplicando nuestra fórmula de derivación, obtendremos.

$\displaystyle y'=\frac{\frac{d}{dx}\left( 8x+3 \right)}{8x+3}$

Derivando en la parte del numerador, nos daría el resultado que deseamos.

Resultado:

$\displaystyle y'=\frac{8}{8x+3}$

Ejemplo 3. Resuelva la siguiente derivada

$\displaystyle y=\ln \left( 3{{x}^{2}}-3x+7 \right)$

Solución:

Al observar nuestra función y su argumento, nos percatamos que u = 3x² - 3x +7 , entonces al aplicar la fórmula de derivada, obtenemos.

$\displaystyle y'=\frac{\frac{d\left( 3{{x}^{2}}-3x+7 \right)}{dx}}{3{{x}^{2}}-3x+7}$

Derivamos en la parte del numerador y esto nos da, el resultado

Resultado:

$\displaystyle y=\frac{6x-3}{3{{x}^{2}}-3x+7}$

Ejemplo 4. Resuelva la siguiente derivada

$\displaystyle y=\ln \sqrt{9x}$

Solución:

Al analizar nuestro argumento es u = √9x , de tal forma que al aplicar nuestra fórmula de derivada, obtenemos.

$\displaystyle y'=\frac{\frac{d}{dx}\sqrt{9x}}{\sqrt{9x}}$

Pasamos a la raíz cuadrada a su forma de potencia, es decir:

$\displaystyle y'=\frac{\frac{d}{dx}{{\left( 9x \right)}^{\frac{1}{2}}}}{\sqrt{9x}}$

Derivamos como una potencia y esto nos daría:

$\displaystyle y'=\frac{\frac{1}{2}{{\left( 9x \right)}^{\frac{1}{2}-1}}\frac{d}{dx}\left( 9x \right)}{\sqrt{9x}}$

Resolviendo...

$\displaystyle y'=\frac{\frac{1}{2}{{\left( 9x \right)}^{-\frac{1}{2}}}\left( 9 \right)}{\sqrt{9x}}$

Ordenando la parte del numerador.

$\displaystyle y'=\frac{\frac{9}{2\sqrt{9x}}}{\sqrt{9x}}$

Aplicando la ley de la torta, el sandwich o la herradura, como le llamen, obtenemos:

$\displaystyle y'=\frac{9}{2\sqrt{9x}\sqrt{9x}}$

Al multiplicar las dos raíces nos daría las raíces al cuadrado, lo que lo simplificaría a 1 , de tal forma:

$\displaystyle y'=\frac{9}{2{{\left( \sqrt{9x} \right)}^{2}}}=\frac{9}{2\left( 9x \right)}$

Simplificando aún más, obtenemos nuestro resultado.

Resultado:

$\displaystyle y'=\frac{1}{2x}$

🔥 Otra forma de Solución

Como sabemos que

$\displaystyle y=\ln \sqrt{9x}=\ln {{\left( 9x \right)}^{\frac{1}{2}}}$

Si aplicamos la 3ra propiedad de los logaritmos, obtenemos lo siguiente:

$\displaystyle y=\frac{1}{2}\ln \left( 9x \right)$

Al derivar esta función, nos percatamos que 1/2 es constante, por lo tanto lo ponemos detrás de la función a derivar, de esta forma:

$\displaystyle {y}'=\frac{1}{2}\left[ \frac{\frac{d}{dx}9x}{9x} \right]$

$\displaystyle {y}'=\frac{1}{2}\left[ \frac{9}{9x} \right]$

Derivando . . .

$\displaystyle y'=\frac{1}{2}\left( \frac{1}{x} \right)=\frac{1}{2x}$

Ejemplo 5. Resuelva la siguiente derivada

$\displaystyle y=\ln \left( \frac{1}{\sqrt[3]{6{{x}^{2}}}} \right)$

Solución:

Para este ejemplo observamos que nuestro argumento es:

$\displaystyle u=\frac{1}{\sqrt[3]{6{{x}^{2}}}}$

Por lo que al aplicar nuestra fórmula de derivada, obtendremos algo similar a esto:

$\displaystyle y'=\frac{\frac{d}{dx}\left( \frac{1}{\sqrt[3]{6{{x}^{2}}}} \right)}{\frac{1}{\sqrt[3]{6{{x}^{2}}}}}$

Pasando a nuestro numerador en forma de potencia, obtenemos lo siguiente:

$\displaystyle y'=\frac{\frac{d}{dx}{{\left( 6{{x}^{2}} \right)}^{-\frac{1}{3}}}}{\frac{1}{\sqrt[3]{6{{x}^{2}}}}}$

Aplicamos la fórmula de derivada para una potencia, y obtenemos:

$\displaystyle y'=\frac{-\frac{1}{3}{{\left( 6{{x}^{2}} \right)}^{-\frac{1}{3}-1}}\frac{d}{dx}\left( 6{{x}^{2}} \right)}{\frac{1}{\sqrt[3]{6{{x}^{2}}}}}$

Luego, hacemos . . .

$\displaystyle y'=\frac{-\frac{1}{3}{{\left( 6{{x}^{2}} \right)}^{-\frac{4}{3}}}\left( 12x \right)}{\frac{1}{\sqrt[3]{6{{x}^{2}}}}}$

Aplicamos la identidad recíproca para ordenar la parte del numerador, de esta forma:

$\displaystyle y'=\frac{-\frac{12x}{3{{\left( 6{{x}^{2}} \right)}^{\frac{4}{3}}}}}{\frac{1}{\sqrt[3]{6{{x}^{2}}}}}$

Aplicando la división de cocientes (ley de la herradura, ley del sandwich, ley de la torta, etc. )

$\displaystyle y'=\frac{-12x\sqrt[3]{6{{x}^{2}}}}{3{{\left( 6{{x}^{2}} \right)}^{\frac{4}{3}}}}$

Expresando la raíz del numerador en su forma de potencia, obtenemos.

$\displaystyle y'=\frac{-12x{{\left( 6{{x}^{2}} \right)}^{\frac{1}{3}}}}{3{{\left( 6{{x}^{2}} \right)}^{\frac{4}{3}}}}$

Recordando la ley de las potencias, podemos restar los exponentes que tienen la misma base.

$\displaystyle y'=-\frac{12x}{3}{{\left( 6{{x}^{2}} \right)}^{\frac{1}{3}-\frac{4}{3}}}$

Esto nos daría:

$\displaystyle y'=-\frac{12x}{3}{{\left( 6{{x}^{2}} \right)}^{-\frac{3}{3}}}$

Qué es igual a :

$\displaystyle y'=-\frac{12x}{3}{{\left( 6{{x}^{2}} \right)}^{-1}}=-\frac{12x}{3\left( 6{{x}^{2}} \right)}$

Simplificando esta parte . . .

$\displaystyle y'=-\frac{12x}{18{{x}^{2}}}$

Y después de simplificar aún más nuestro resultado, sería:

Resultado:

$\displaystyle y'=-\frac{2}{3x}$

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

Deja una respuesta Cancelar la respuesta