Diagrama de Caja y Bigotes - Ejercicios Resueltos

¡Hola amigos de Fisimat! 🤓 Si alguna vez te has enfrentado a una montaña de números y has deseado tener una radiografía que te muestre su estructura interna de un solo vistazo, estás en el lugar correcto. En el vasto universo de la estadística y el análisis de datos, existen herramientas que son tan elegantes como potentes. Hoy vamos a explorar una de mis favoritas: el Diagrama de Caja y Bigotes, también conocido como Box Plot.

Puede que su nombre suene un poco peculiar, como sacado de una tienda de mascotas o un cuento infantil, pero no te dejes engañar. Este gráfico es una navaja suiza para visualizar la distribución de datos, identificar valores atípicos y comparar diferentes conjuntos de información de manera rápida y eficaz. En este artículo, no solo desmitificaremos cada componente del diagrama de caja, sino que te guiaremos paso a paso para que puedas construirlo e interpretarlo, es muy útil en ingeniería o simplemente si estás abordando el tema de matemáticas en la preparatoria o bachillerato. ¡Vamos allá! 🚀

¿Qué es Exactamente un Diagrama de Caja y Bigotes?

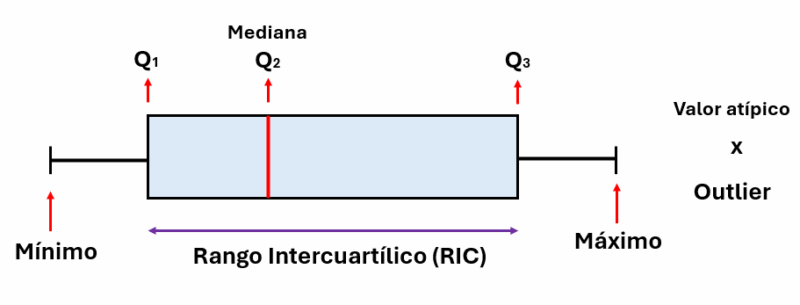
Imagina que tienes los resultados de un examen de 100 estudiantes. Podrías mirar la lista de calificaciones una por una, pero sería difícil hacerte una idea clara de cómo le fue al grupo en general. ¿La mayoría aprobó? ¿Las notas estuvieron muy dispersas? ¿Hubo alguna calificación excepcionalmente alta o baja? Responder a estas preguntas rápidamente es el superpoder del diagrama de caja y bigotes.

En esencia, es una representación gráfica que resume un conjunto de datos utilizando cinco números clave. Estos números dividen los datos en secciones, permitiéndonos entender la dispersión, la tendencia central y la simetría de la distribución. Es como un resumen ejecutivo visual de tu dataset.

Este gráfico nos permite ver de un solo golpe el mínimo, el máximo, la mediana y la concentración de los datos. Es una herramienta fundamental en el Análisis Exploratorio de Datos (EDA), una filosofía que aboga por usar técnicas visuales para desarrollar una comprensión profunda de la información antes de aplicar modelos más complejos.

La Mente Maestra Detrás del Box Plot: John W. Tukey

Toda gran invención tiene un creador brillante, y el diagrama de caja y bigotes no es la excepción. Esta genialidad visual fue introducida por uno de los estadísticos más influyentes del siglo XX.

La filosofía de Tukey era simple: antes de confirmar una hipótesis, primero debemos explorar. El box plot es la encarnación perfecta de esta idea, proporcionando una visión rica y condensada de los datos de forma intuitiva.

Los 5 Números Mágicos: El Corazón del Diagrama de Caja 💛

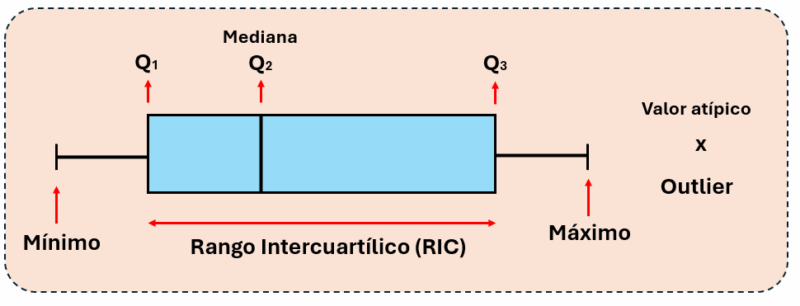
La base de todo diagrama de caja es el "resumen de cinco números". Si entiendes estos cinco valores, entiendes el 90% de un box plot. Vamos a desglosarlos uno por uno.

1. El Mínimo (Min)

Este es el valor más pequeño en tu conjunto de datos, pero con un matiz importante: es el valor más bajo que no se considera un "valor atípico" (outlier). Más adelante veremos cómo se definen estos límites, ¡pero quédate con la idea de que es el punto de partida de nuestros datos "normales"!

2. El Primer Cuartil (Q1)

También conocido como el percentil 25. Este es el valor que deja por debajo al 25% de los datos. Piensa en ello como la "mediana" de la mitad inferior de tu conjunto de datos ordenado. Marca el borde izquierdo de la "caja".

3. La Mediana (Q2)

¡La estrella del espectáculo! 🌟 La mediana es el valor central del conjunto de datos. El 50% de los datos se encuentra por debajo de este valor y el otro 50% por encima. Se representa con una línea que divide la caja en dos. Es una medida de tendencia central más robusta que la media, ya que no se ve afectada por valores extremos.

4. El Tercer Cuartil (Q3)

También conocido como el percentil 75. Este valor deja por debajo al 75% de los datos. Es la "mediana" de la mitad superior de tu conjunto de datos. Marca el borde derecho de la "caja".

5. El Máximo (Max)

Al igual que el mínimo, este es el valor más alto en el conjunto de datos que no se considera un valor atípico. Es el final de nuestro bigote derecho.

Estos cinco números juntos nos dan una estructura sólida, pero hay una pieza más que es crucial para la construcción y la interpretación: el Rango Intercuartílico.

El Rango Intercuartílico (RIC o IQR)

Este concepto es fundamental, especialmente para entender la dispersión y los valores atípicos.

Un RIC pequeño indica que el 50% central de los datos está muy agrupado, mientras que un RIC grande sugiere que esos datos están más dispersos. Lo más importante es que el RIC es la base para definir los límites de los "bigotes" y cazar a los outliers.

Construyendo tu Primer Diagrama de Caja y Bigotes: Guía Paso a Paso 🛠️

¡Basta de teoría! Es hora de arremangarse y construir un diagrama de caja desde cero. Usaremos un conjunto de datos de ejemplo para que puedas seguir cada paso. Supongamos que tenemos las calificaciones de 15 estudiantes en un examen de física:

Calificaciones: {82, 95, 65, 78, 88, 72, 91, 85, 76, 99, 58, 81, 93, 79, 84}

Solución:

Seguiremos un proceso metódico de 6 pasos para construir nuestro diagrama.

Paso 1: Ordenar los Datos
El primer paso, y el más crucial, es ordenar los datos de menor a mayor.

{58, 65, 72, 76, 78, 79, 81, 82, 84, 85, 88, 91, 93, 95, 99}

Paso 2: Calcular la Mediana (Q2)
La mediana es el valor que se encuentra justo en el medio. Como tenemos 15 datos (un número impar), la mediana será el valor en la posición \((n+1)/2\). En nuestro caso, \((15+1)/2 = 8\). El octavo valor en nuestra lista ordenada es la mediana.

\[ Q2 (\text{Mediana}) = 82 \]

Paso 3: Calcular los Cuartiles (Q1 y Q3)
Ahora dividimos el conjunto de datos en dos mitades (sin incluir la mediana):

• Mitad Inferior: {58, 65, 72, 76, 78, 79, 81}
• Mitad Superior: {84, 85, 88, 91, 93, 95, 99}

Q1 es la mediana de la mitad inferior. Como hay 7 datos, la mediana es el cuarto valor.

\[ Q1 = 76 \]

Q3 es la mediana de la mitad superior. De nuevo, con 7 datos, es el cuarto valor.

\[ Q3 = 91 \]

Paso 4: Calcular el Rango Intercuartílico (RIC)
Ahora usamos la fórmula que aprendimos.

\[ RIC = Q3 - Q1 = 91 - 76 = 15 \]

Esto nos dice que el 50% central de las calificaciones se encuentra en un rango de 15 puntos.

Paso 5: Identificar los "Bigotes" y Posibles Outliers
Para encontrar los límites de nuestros bigotes, usamos el RIC. La regla estándar es 1.5 veces el RIC por debajo de Q1 y por encima de Q3.

• Límite Inferior: \( Q1 - 1.5 \times RIC = 76 - 1.5 \times 15 = 76 - 22.5 = 53.5 \)
• Límite Superior: \( Q3 + 1.5 \times RIC = 91 + 1.5 \times 15 = 91 + 22.5 = 113.5 \)

Ahora, buscamos en nuestro conjunto de datos ordenado:

• El valor más pequeño que sea mayor o igual a 53.5 es 58. Este será nuestro Mínimo (el final del bigote inferior).
• El valor más grande que sea menor o igual a 113.5 es 99. Este será nuestro Máximo (el final del bigote superior).

En este caso, todos nuestros datos caen dentro de estos límites, por lo que no hay outliers. Si tuviéramos una calificación de 50, por ejemplo, estaría por debajo de 53.5 y la marcaríamos como un outlier.

Paso 6: Dibujar el Diagrama
Con nuestros 5 números mágicos listos (Mínimo=58, Q1=76, Mediana=82, Q3=91, Máximo=99), podemos dibujar el gráfico:

1. Dibuja una escala numérica horizontal que abarque el rango de tus datos (por ejemplo, de 50 a 100).
2. Dibuja una caja rectangular con el borde izquierdo en Q1 (76) y el borde derecho en Q3 (91).
3. Dibuja una línea vertical dentro de la caja en la Mediana (82).
4. Dibuja una línea horizontal (el "bigote") desde el borde izquierdo de la caja (Q1) hasta el Mínimo (58).
5. Dibuja otro bigote desde el borde derecho de la caja (Q3) hasta el Máximo (99).
6. Si hubiera outliers, los marcarías con puntos o asteriscos fuera de los bigotes.

¡Y listo! 🎉 Acabas de construir tu primer diagrama de caja y bigotes.

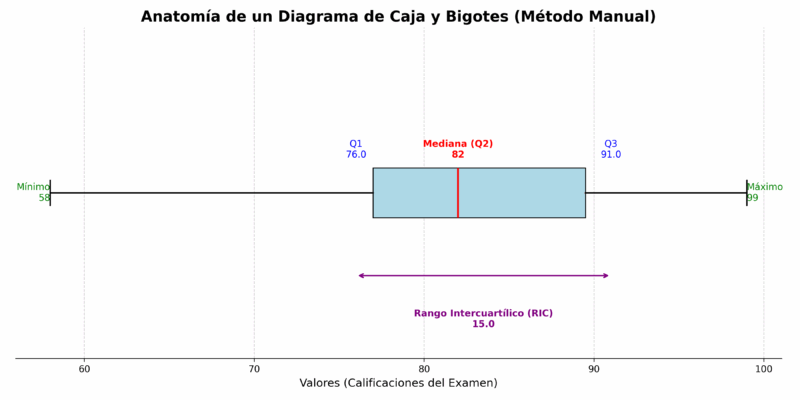
Interpretando el Diagrama de Caja: ¿Qué Nos Dicen los Datos? 🕵️‍♂️

Un diagrama de caja es mucho más que un simple dibujo. Es una fuente de información valiosa. Veamos qué podemos deducir de nuestro ejemplo y en general.

• Centralidad: La línea de la mediana (82) nos dice el "centro" de las calificaciones. El 50% de los estudiantes sacó 82 o menos, y el otro 50% sacó 82 o más.
• Dispersión: La longitud de la caja (RIC = 15) nos indica la variabilidad del 50% central de los estudiantes. Una caja más ancha significaría más dispersión en las notas del "estudiante promedio".
• Asimetría (Skewness): Observa la posición de la mediana dentro de la caja y la longitud de los bigotes.
  • La mediana (82) está ligeramente a la izquierda del centro de la caja (el centro estaría en (76+91)/2 = 83.5). Esto sugiere una leve asimetría positiva (sesgo a la derecha).
  • El bigote derecho (de 91 a 99, longitud 8) es más corto que el bigote izquierdo (de 58 a 76, longitud 18). Esto, en cambio, sugiere una asimetría negativa (sesgo a la izquierda), ya que la cola de datos más bajos está más extendida.
  • Cuando hay señales contradictorias, significa que la asimetría no es muy pronunciada.
• Outliers: Como vimos, en nuestro caso no hay outliers. Si los hubiera, nos indicarían calificaciones inusualmente altas o bajas que podrían merecer una investigación más detallada. ¿El estudiante hizo trampa? ¿O tuvo un mal día?

La verdadera magia de los box plots aparece cuando comparas varios conjuntos de datos uno al lado del otro.

¡Excelente! Ahora que hemos dominado la construcción de nuestro primer diagrama, vamos a reforzar nuestras habilidades con tres ejercicios adicionales. Cada uno presenta un escenario ligeramente diferente para asegurarnos de que podemos manejar cualquier conjunto de datos que se nos presente. 🧠💪

Solución:

Este caso es interesante porque tenemos un número par de datos (12), lo que cambia ligeramente el cálculo de la mediana y los cuartiles.

Paso 1: Ordenar los Datos
Primero, organizamos los datos de menor a mayor.

{38, 40, 45, 50, 55, 60, 65, 70, 75, 80, 95, 110}

Paso 2: Calcular la Mediana (Q2)
Con 12 datos, no hay un único valor central. La mediana es el promedio de los dos valores centrales (el 6º y el 7º).

\[ Q2 (\text{Mediana}) = \frac{60 + 65}{2} = 62.5 \]

Paso 3: Calcular los Cuartiles (Q1 y Q3)
Dividimos los datos en dos mitades, usando la mediana como punto de corte. Cada mitad tendrá 6 datos.

• Mitad Inferior: {38, 40, 45, 50, 55, 60}
• Mitad Superior: {65, 70, 75, 80, 95, 110}

Q1 es la mediana de la mitad inferior. De nuevo, es el promedio de los dos valores centrales (el 3º y el 4º).

\[ Q1 = \frac{45 + 50}{2} = 47.5 \]

Q3 es la mediana de la mitad superior (el 3º y 4º de esa mitad, que son el 9º y 10º de la lista original).

\[ Q3 = \frac{75 + 80}{2} = 77.5 \]

Paso 4: Calcular el Rango Intercuartílico (RIC)
Calculamos la diferencia entre Q3 y Q1.

\[ RIC = Q3 - Q1 = 77.5 - 47.5 = 30 \]

Paso 5: Identificar los "Bigotes" y Posibles Outliers
Usamos la regla de \(1.5 \times RIC\) para definir los límites.

• Límite Inferior: \( Q1 - 1.5 \times RIC = 47.5 - 1.5 \times 30 = 47.5 - 45 = 2.5 \)
• Límite Superior: \( Q3 + 1.5 \times RIC = 77.5 + 1.5 \times 30 = 77.5 + 45 = 122.5 \)

Ahora, revisamos nuestros datos ordenados:

• El valor más pequeño que es mayor o igual a 2.5 es 38 (nuestro Mínimo).
• El valor más grande que es menor o igual a 122.5 es 110 (nuestro Máximo).

Todos los datos caen dentro de los límites, por lo que no hay outliers.

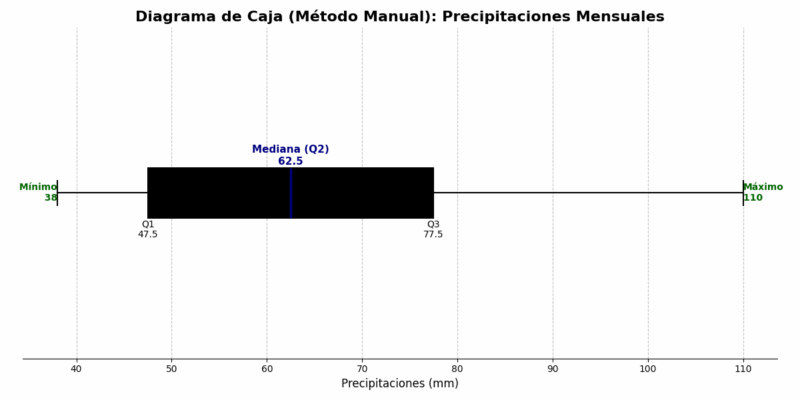
Paso 6: Dibujar el Diagrama
Con nuestros 5 números (Mínimo=38, Q1=47.5, Mediana=62.5, Q3=77.5, Máximo=110), procederemos a generar la gráfica.

Solución:

Este ejemplo es perfecto para ver cómo el diagrama de caja resalta los valores inusuales.

Paso 1: Ordenar los Datos
{185, 190, 198, 205, 210, 215, 225, 230, 240, 310}

Paso 2: Calcular la Mediana (Q2)
Tenemos 10 datos (par), así que promediamos los dos centrales (el 5º y el 6º).

\[ Q2 (\text{Mediana}) = \frac{210 + 215}{2} = 212.5 \]

Paso 3: Calcular los Cuartiles (Q1 y Q3)
Dividimos los datos en dos mitades de 5.

• Mitad Inferior: {185, 190, 198, 205, 210}
• Mitad Superior: {215, 225, 230, 240, 310}

Q1 es la mediana de la mitad inferior (el 3er valor).

\[ Q1 = 198 \]

Q3 es la mediana de la mitad superior (el 3er valor de esa mitad).

\[ Q3 = 230 \]

Paso 4: Calcular el Rango Intercuartílico (RIC)

\[ RIC = Q3 - Q1 = 230 - 198 = 32 \]

Paso 5: Identificar los "Bigotes" y Posibles Outliers
Calculamos los límites.

• Límite Inferior: \( Q1 - 1.5 \times RIC = 198 - 1.5 \times 32 = 198 - 48 = 150 \)
• Límite Superior: \( Q3 + 1.5 \times RIC = 230 + 1.5 \times 32 = 230 + 48 = 278 \)

Revisemos nuestros datos:

• El valor más pequeño mayor o igual a 150 es 185. Este es el Mínimo y el final del bigote inferior.
• El valor más grande menor o igual a 278 es 240. Este es el Máximo "normal" y el final del bigote superior.

¡Atención! 🚨 El valor 310 es mayor que nuestro límite superior de 278. Por lo tanto, 310 es un valor atípico (outlier). En el gráfico, se representará como un punto separado.

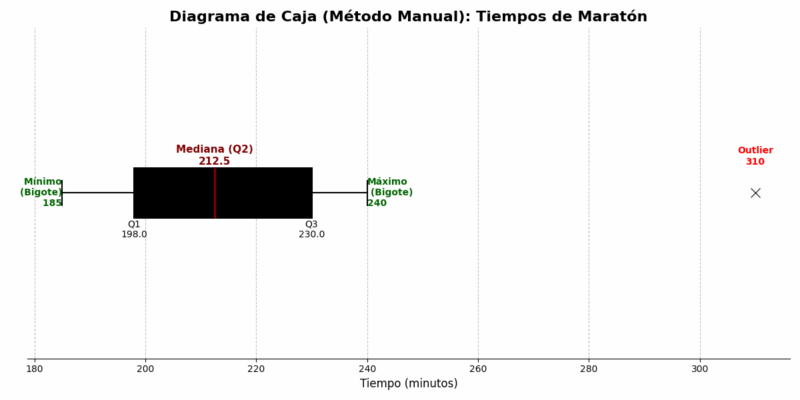
Paso 6: Dibujar el Diagrama
Nuestros 5 números para la caja y los bigotes son: Mínimo=185, Q1=198, Mediana=212.5, Q3=230, Máximo (del bigote)=240. Adicionalmente, marcaremos un outlier en 310.

Solución:

Este conjunto de datos nos ayudará a interpretar la asimetría.

Paso 1: Ordenar los Datos
{35, 40, 42, 45, 48, 50, 52, 55, 60, 65, 70, 95}

Paso 2: Calcular la Mediana (Q2)
Con 12 datos, promediamos el 6º y 7º valor.

\[ Q2 (\text{Mediana}) = \frac{50 + 52}{2} = 51 \]

Paso 3: Calcular los Cuartiles (Q1 y Q3)
Dividimos en dos mitades de 6 datos.

• Mitad Inferior: {35, 40, 42, 45, 48, 50}
• Mitad Superior: {52, 55, 60, 65, 70, 95}

\[ Q1 = \frac{42 + 45}{2} = 43.5 \]

\[ Q3 = \frac{60 + 65}{2} = 62.5 \]

Paso 4: Calcular el Rango Intercuartílico (RIC)

\[ RIC = Q3 - Q1 = 62.5 - 43.5 = 19 \]

Paso 5: Identificar los "Bigotes" y Posibles Outliers
Calculamos los límites.

• Límite Inferior: \( Q1 - 1.5 \times RIC = 43.5 - 1.5 \times 19 = 43.5 - 28.5 = 15 \)
• Límite Superior: \( Q3 + 1.5 \times RIC = 62.5 + 1.5 \times 19 = 62.5 + 28.5 = 91 \)

Revisamos nuestros datos:

• El mínimo es 35, que está dentro del límite.
• El valor más grande que es menor o igual a 91 es 70. Este será el final de nuestro bigote superior.
• El valor 95 es mayor que 91, por lo que es un outlier.

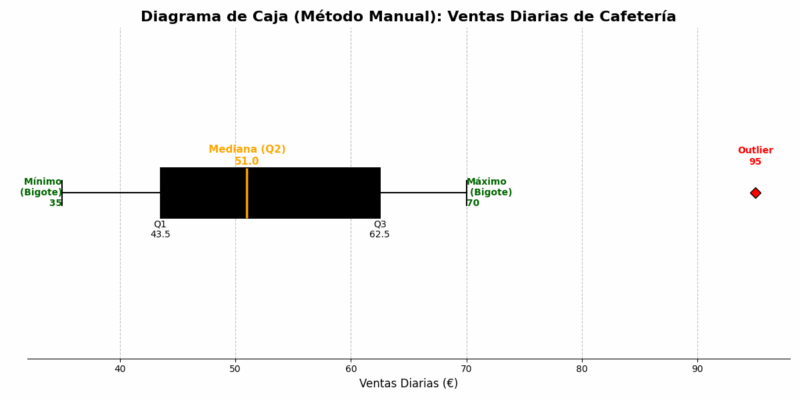
Paso 6: Dibujar el Diagrama
Los componentes son: Mínimo=35, Q1=43.5, Mediana=51, Q3=62.5, Máximo (del bigote)=70, y un outlier en 95. La distancia de la mediana a Q3 (11.5) es mayor que la distancia a Q1 (7.5), y el bigote superior (de 62.5 a 70) junto con el outlier en 95 nos muestran una clara asimetría positiva (sesgo a la derecha), indicando que hay algunos días con ventas inusualmente altas.

Interpretación:

"Envío Veloz" es, en promedio, más rápido (mediana más baja), pero es muy inconsistente. Su tiempo de entrega es impredecible (caja y bigotes largos), y a veces falla estrepitosamente (outliers). Por otro lado, "Paquete Seguro" es un poco más lento, pero es extremadamente consistente y fiable. Casi todas sus entregas llegan alrededor de los 4 días. La elección entre ambos dependería de si priorizas la velocidad potencial o la fiabilidad.

Ventajas y Desventajas del Diagrama de Caja y Bigotes

Como toda herramienta, el box plot tiene sus puntos fuertes y sus limitaciones.

Ventajas 👍

• Comparación Eficaz: Son inmejorables para comparar las distribuciones de varios grupos a la vez.
• Resumen Conciso: Muestran una gran cantidad de información (centro, dispersión, asimetría, outliers) en un formato compacto.
• Robustez: Al basarse en la mediana y los cuartiles, no se ven afectados por valores extremos, lo que los hace ideales para datos con distribuciones no normales.
• Identificación de Outliers: El método del \(1.5 \times RIC\) es una forma estandarizada y efectiva de señalar puntos de datos que podrían necesitar una revisión.

Desventajas 👎

• Simplificación Excesiva: Pueden ocultar ciertas características de la distribución, como la bimodalidad (distribuciones con dos picos). Un histograma o un gráfico de densidad podría ser mejor en esos casos.
• Ambigüedad con el Tamaño de Muestra: Un box plot para 10 puntos de datos puede verse idéntico a uno para 10,000 puntos, lo que puede ser engañoso.
• No Muestra Datos Individuales: Aparte de los outliers, no se ven los puntos de datos individuales, solo el resumen.

Conclusión: La Herramienta Visual Definitiva para el Análisis de Datos

El diagrama de caja y bigotes es mucho más que una simple curiosidad estadística; es una herramienta de visualización extraordinariamente potente y versátil. Desde sus raíces en el trabajo pionero de John W. Tukey hasta su aplicación diaria en campos que van desde la ingeniería y las finanzas hasta la biología, el box plot nos demuestra que una imagen bien construida puede valer más que mil números.

Ahora tienes el conocimiento y la guía para no solo leer, sino también construir tus propios diagramas de caja. La próxima vez que te enfrentes a un conjunto de datos, te animo a que apliques estos pasos. Dibuja el box plot y escucha la historia que los datos quieren contarte. Te sorprenderá la claridad y las ideas que puedes obtener de esta pequeña y elegante "caja" con "bigotes". ¡Feliz análisis! 📊