División de Fracciones - Ejercicios Resueltos

¡Qué tal amigos de Fisimat!, hoy hablaremos sobre la división de fracciones es, a menudo, la operación que genera más dudas entre los estudiantes, pero en realidad, es tan sencilla como la multiplicación, una vez que conoces el truco. A diferencia de los números enteros, donde la división a veces resulta en un resto, dividir fracciones es como preguntarse cuántas veces "cabe" una parte de un todo en otra parte. Imagina que tienes media pizza y quieres saber cuántas porciones de un cuarto puedes sacar de ella.

Dominar la división de fracciones es una habilidad esencial que te abrirá las puertas a conceptos matemáticos más complejos y te permitirá resolver problemas prácticos en diversas áreas. Desde la repartición equitativa de recursos hasta el escalado de proporciones en el diseño o la resolución de ecuaciones en física y robótica, la división de fracciones tiene un sinfín de aplicaciones. En este artículo, desglosaremos el método simple para dividir fracciones y te ofreceremos una serie de ejercicios resueltos para que te sientas completamente seguro al realizarlas.

La división de fracciones se resuelve transformándola en una multiplicación. 🤓

Regla General para Dividir Fracciones: Multiplicar por el Recíproco

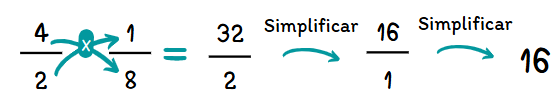
La regla fundamental para dividir fracciones es:

1. Mantén la primera fracción (el dividendo) tal como está.
2. Cambia la operación de división ($\div$) a multiplicación ($\times$).
3. Invierte la segunda fracción (el divisor). Para invertir una fracción, simplemente intercambia su numerador y su denominador. Esta nueva fracción se llama el recíproco o inverso multiplicativo.
4. Multiplica las dos fracciones resultantes como lo harías normalmente (numerador por numerador y denominador por denominador).
5. Simplifica la fracción final a su mínima expresión si es posible.

1. 1. Primera fracción se mantiene: $\frac{3}{4}$.
   2. Cambiar a multiplicación: $\times$.
   3. Invertir la segunda fracción: El recíproco de $\frac{2}{5}$ es $\frac{5}{2}$.
   4. Multiplicar:
      $$\frac{3}{4} \times \frac{5}{2} = \frac{3 \times 5}{4 \times 2} = \frac{15}{8}$$
   5. Convertir a número mixto (opcional):
      $$\frac{15}{8} = 1\frac{7}{8}$$

División de Fracciones con Números Enteros

Cuando dividimos una fracción por un número entero o viceversa, tratamos al número entero como una fracción con denominador 1.

Fracción dividida por un Entero

1. 1. Convertir el entero a fracción: $3 = \frac{3}{1}$.
   2. Aplicar la regla: mantener $\frac{6}{7}$, cambiar a $\times$, invertir $\frac{3}{1}$ a $\frac{1}{3}$.
   3. Multiplicar:
      $$\frac{6}{7} \times \frac{1}{3} = \frac{6 \times 1}{7 \times 3} = \frac{6}{21}$$
   4. Simplificar: El MCD de 6 y 21 es 3.
      $$\frac{6 \div 3}{21 \div 3} = \frac{2}{7}$$

Entero dividido por una Fracción

1. Convertir el entero a fracción: $5 = \frac{5}{1}$.
2. Aplicar la regla: mantener $\frac{5}{1}$, cambiar a $\times$, invertir $\frac{1}{2}$ a $\frac{2}{1}$.
3. Multiplicar:
   $$\frac{5}{1} \times \frac{2}{1} = \frac{5 \times 2}{1 \times 1} = \frac{10}{1} = 10$$

Esto tiene sentido: ¿cuántas "mitades" hay en 5 enteros? Diez mitades.

División de Fracciones con Números Mixtos

Cuando la división involucra números mixtos, el primer paso es siempre convertirlos a fracciones impropias.

1. Convierte todos los números mixtos a fracciones impropias.
2. Aplica la regla general de la división (mantener la primera, cambiar a multiplicar, invertir la segunda).
3. Multiplica las fracciones impropias.
4. Simplifica el resultado y, si es una fracción impropia, conviértela a número mixto (opcional).

1. 1. Convertir a impropias:
      $$2\frac{1}{2} = \frac{(2 \times 2) + 1}{2} = \frac{5}{2}$$
      $$1\frac{1}{4} = \frac{(1 \times 4) + 1}{4} = \frac{5}{4}$$
   2. Aplicar la regla:
      $$\frac{5}{2} \div \frac{5}{4} = \frac{5}{2} \times \frac{4}{5}$$
   3. Multiplicar y simplificar previamente (el 5 con el 5, el 2 con el 4):
      $$\frac{5 \div 5}{2 \div 2} \times \frac{4 \div 2}{5 \div 5} = \frac{1}{1} \times \frac{2}{1}$$
   4. Resultado:
      $$\frac{1 \times 2}{1 \times 1} = \frac{2}{1} = 2$$

Ejercicios Resueltos de División de Fracciones

Refuerza tus habilidades con estos ejercicios de división de fracciones.

Solución

▷ Paso 1 Mantener la primera fracción y cambiar la operación.
$$\frac{7}{9} \times $$

▷ Paso 2 Invertir la segunda fracción.
El recíproco de $\frac{2}{3}$ es $\frac{3}{2}$.
$$\frac{7}{9} \times \frac{3}{2}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz si es posible).
El 3 (numerador de la segunda) y el 9 (denominador de la primera) son divisibles por 3.
$$\frac{7}{9 \div 3} \times \frac{3 \div 3}{2} = \frac{7}{3} \times \frac{1}{2}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{7 \times 1}{3 \times 2} = \frac{7}{6}$$

▷ Paso 5 Convertir a número mixto (opcional).
$$\frac{7}{6} = 1\frac{1}{6}$$

Por lo tanto, $\frac{7}{9} \div \frac{2}{3} = \frac{7}{6}$ o $1\frac{1}{6}$.

Solución

▷ Paso 1 Convertir el número entero a fracción.
$$10 = \frac{10}{1}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{10}{1} \times \frac{2}{5}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz).
El 10 (numerador de la primera) y el 5 (denominador de la segunda) son divisibles por 5.
$$\frac{10 \div 5}{1} \times \frac{2}{5 \div 5} = \frac{2}{1} \times \frac{2}{1}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{2 \times 2}{1 \times 1} = \frac{4}{1} = 4$$

Por lo tanto, $10 \div \frac{5}{2} = 4$.

Solución

▷ Paso 1 Convertir el número entero a fracción.
$$2 = \frac{2}{1}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{4}{5} \times \frac{1}{2}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz).
El 4 (numerador de la primera) y el 2 (denominador de la segunda) son divisibles por 2.
$$\frac{4 \div 2}{5} \times \frac{1}{2 \div 2} = \frac{2}{5} \times \frac{1}{1}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{2 \times 1}{5 \times 1} = \frac{2}{5}$$

Por lo tanto, $\frac{4}{5} \div 2 = \frac{2}{5}$.

Solución

▷ Paso 1 Convertir los números mixtos a fracciones impropias.
$$3\frac{1}{3} = \frac{(3 \times 3) + 1}{3} = \frac{10}{3}$$
$$1\frac{1}{2} = \frac{(1 \times 2) + 1}{2} = \frac{3}{2}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{10}{3} \times \frac{2}{3}$$

▷ Paso 3 Multiplicar los numeradores y denominadores (no hay simplificación en cruz).
$$\frac{10 \times 2}{3 \times 3} = \frac{20}{9}$$

▷ Paso 4 Convertir a número mixto (opcional).
$$\frac{20}{9} = 2\frac{2}{9}$$

Por lo tanto, $3\frac{1}{3} \div 1\frac{1}{2} = \frac{20}{9}$ o $2\frac{2}{9}$.

Solución

Para saber cuántas porciones pueden obtener, dividimos la cantidad total de pizza por el tamaño de cada porción.

▷ Paso 1 Plantear la división.
$$\frac{5}{2} \div \frac{1}{4}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{5}{2} \times \frac{4}{1}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz).
El 4 (numerador de la segunda) y el 2 (denominador de la primera) son divisibles por 2.
$$\frac{5}{2 \div 2} \times \frac{4 \div 2}{1} = \frac{5}{1} \times \frac{2}{1}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{5 \times 2}{1 \times 1} = \frac{10}{1} = 10$$

Respuesta: Pueden obtener 10 porciones de pizza.

Solución

Para saber cuántos trozos se obtienen, dividimos la longitud total del rollo por la longitud de cada trozo.

▷ Paso 1 Plantear la división, convirtiendo el entero a fracción.
$$12 \div \frac{3}{4} = \frac{12}{1} \div \frac{3}{4}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{12}{1} \times \frac{4}{3}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz).
El 12 (numerador de la primera) y el 3 (denominador de la segunda) son divisibles por 3.
$$\frac{12 \div 3}{1} \times \frac{4}{3 \div 3} = \frac{4}{1} \times \frac{4}{1}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{4 \times 4}{1 \times 1} = \frac{16}{1} = 16$$

Respuesta: Se pueden obtener 16 trozos de tela.

Solución

Para saber cuántos vasos se pueden llenar, dividimos el volumen total de jugo por el volumen de cada vaso.

▷ Paso 1 Plantear la división.
$$\frac{7}{8} \div \frac{1}{16}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{7}{8} \times \frac{16}{1}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz).
El 16 (numerador de la segunda) y el 8 (denominador de la primera) son divisibles por 8.
$$\frac{7}{8 \div 8} \times \frac{16 \div 8}{1} = \frac{7}{1} \times \frac{2}{1}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{7 \times 2}{1 \times 1} = \frac{14}{1} = 14$$

Respuesta: Se pueden llenar 14 vasos.

Solución

La velocidad promedio se calcula dividiendo la distancia recorrida por el tiempo empleado.

▷ Paso 1 Convertir la distancia mixta a fracción impropia.
$$2\frac{1}{2} = \frac{(2 \times 2) + 1}{2} = \frac{5}{2} \text{ km}$$

▷ Paso 2 Plantear la división: $\text{Distancia} \div \text{Tiempo}$.
$$\frac{5}{2} \div \frac{1}{4}$$

▷ Paso 3 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{5}{2} \times \frac{4}{1}$$

▷ Paso 4 Multiplicar las fracciones (simplificando en cruz).
El 4 (numerador de la segunda) y el 2 (denominador de la primera) son divisibles por 2.
$$\frac{5}{2 \div 2} \times \frac{4 \div 2}{1} = \frac{5}{1} \times \frac{2}{1}$$

▷ Paso 5 Realizar la multiplicación final.
$$\frac{5 \times 2}{1 \times 1} = \frac{10}{1} = 10$$

Respuesta: La velocidad promedio del ciclista es $10$ km/h.

Solución

Para saber cuántas veces cabe una fracción en otra, dividimos la fracción mayor por la fracción menor.

▷ Paso 1 Plantear la división.
$$\frac{9}{5} \div \frac{3}{10}$$

▷ Paso 2 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{9}{5} \times \frac{10}{3}$$

▷ Paso 3 Multiplicar las fracciones (simplificando en cruz).
El 9 (numerador de la primera) y el 3 (denominador de la segunda) son divisibles por 3.
$$\frac{9 \div 3}{5} \times \frac{10}{3 \div 3} = \frac{3}{5} \times \frac{10}{1}$$
El 10 (numerador de la segunda) y el 5 (denominador de la primera) son divisibles por 5.
$$\frac{3}{5 \div 5} \times \frac{10 \div 5}{1} = \frac{3}{1} \times \frac{2}{1}$$

▷ Paso 4 Realizar la multiplicación final.
$$\frac{3 \times 2}{1 \times 1} = \frac{6}{1} = 6$$

Respuesta: $\frac{3}{10}$ cabe 6 veces en $\frac{9}{5}$.

Solución

Para saber cuántas bolsas se pueden llenar, dividimos la cantidad total de arroz por la capacidad de cada bolsa.

▷ Paso 1 Convertir la cantidad total de arroz a fracción impropia.
$$4\frac{1}{2} = \frac{(4 \times 2) + 1}{2} = \frac{9}{2} \text{ kg}$$

▷ Paso 2 Plantear la división.
$$\frac{9}{2} \div \frac{3}{4}$$

▷ Paso 3 Mantener la primera fracción, cambiar la operación e invertir la segunda.
$$\frac{9}{2} \times \frac{4}{3}$$

▷ Paso 4 Multiplicar las fracciones (simplificando en cruz).
El 9 (numerador de la primera) y el 3 (denominador de la segunda) son divisibles por 3.
$$\frac{9 \div 3}{2} \times \frac{4}{3 \div 3} = \frac{3}{2} \times \frac{4}{1}$$
El 4 (numerador de la segunda) y el 2 (denominador de la primera) son divisibles por 2.
$$\frac{3}{2 \div 2} \times \frac{4 \div 2}{1} = \frac{3}{1} \times \frac{2}{1}$$

▷ Paso 5 Realizar la multiplicación final.
$$\frac{3 \times 2}{1 \times 1} = \frac{6}{1} = 6$$

Respuesta: Se pueden llenar 6 bolsas de arroz.

Conclusión

La división de fracciones, una vez que se entiende el concepto de "multiplicar por el recíproco", se revela como una de las operaciones más directas y, en muchos casos, la más sencilla de todas. Esta técnica transforma un problema de división en uno de multiplicación, lo cual a menudo puede simplificarse aún más mediante la cancelación cruzada antes de realizar los productos finales.

Dominar esta operación es crucial para una comprensión profunda de las relaciones entre números y para resolver una amplia gama de problemas que involucran el reparto de cantidades, el cálculo de proporciones por unidad, y la aplicación de conceptos en física, ingeniería, robótica y otras áreas donde la división de cantidades fraccionarias es común. Con la práctica constante, la división de fracciones se convertirá en una herramienta intuitiva en tu repertorio matemático. ¡Has completado con éxito la serie de operaciones con fracciones!