Fracciones Operaciones Básicas - Ejercicios Resueltos

¡Hola amigos de Fisimat! hoy hablaremos de un tema fundamental en aritmética, y esto es porque en el mundo de las matemáticas, no siempre trabajamos con números enteros. A menudo nos encontramos con situaciones donde necesitamos representar partes de un todo, como la mitad de una pizza, un cuarto de hora o tres cuartos de un litro de leche. Para estas situaciones, las fracciones se convierten en una herramienta indispensable. Una fracción es una forma de expresar una cantidad dividida por otra cantidad, donde la cantidad superior (numerador) representa las partes que tomamos, y la cantidad inferior (denominador) representa el total de partes iguales en que se divide la unidad.

Si quieres aprender por separado cada concepto de las operaciones de fracciones, lo puedes hacer desde aquí:

✅ Conversión de Fracciones Impropias a Mixtas y Viceversa - Ejercicios Resueltos

✅ Suma y Resta de Fracciones - Ejercicios Resueltos

✅ Multiplicación de Fracciones - Ejercicios Resueltos

✅ División de Fracciones - Ejercicios Resueltos

Comprender las fracciones y dominar sus operaciones básicas es fundamental en tu trayectoria académica, ya que son la base para el estudio de números racionales, porcentajes, proporciones y muchos conceptos en álgebra. Además, su aplicación es constante en la vida cotidiana, la ingeniería e incluso la robótica, al momento de calcular proporciones, repartir elementos o escalar medidas. En este artículo, exploraremos qué son las fracciones, sus tipos y cómo realizar las operaciones fundamentales con ellas. 🤓

Las fracciones son una manera poderosa de representar números que no son enteros. Para entenderlas mejor, es crucial conocer sus componentes y clasificaciones.

Concepto de Fracción

Una fracción se compone de dos números separados por una línea horizontal (o una barra diagonal).

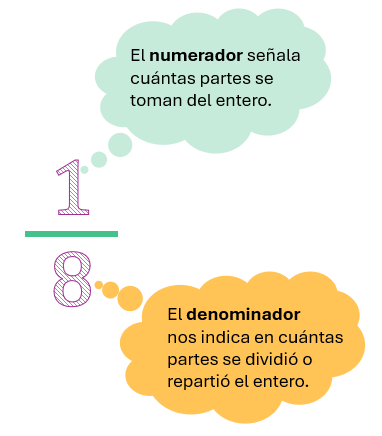
• Numerador: Es el número de arriba. Indica cuántas partes del total se toman o se consideran.
• Denominador: Es el número de abajo. Indica el número total de partes iguales en que se ha dividido la unidad o el todo. El denominador nunca puede ser cero.
• Línea fraccionaria: La línea que separa el numerador del denominador y significa "dividido por".

Ejemplo: La fracción $\frac{3}{4}$ significa que una unidad se ha dividido en 4 partes iguales, y se están tomando 3 de esas partes.

Tipos de Fracciones

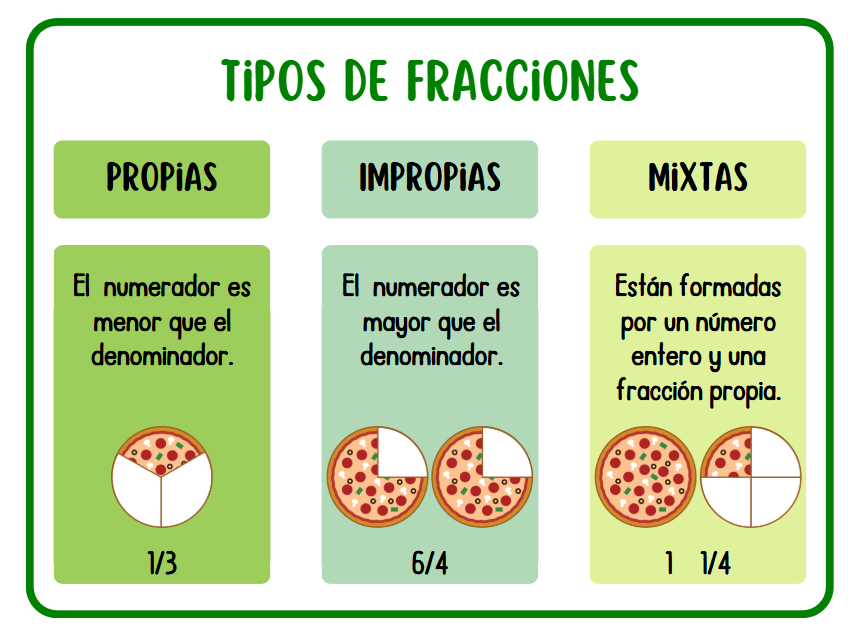
Las fracciones se pueden clasificar en diferentes tipos, cada una con características particulares:

Fracciones Propias

Una fracción es propia cuando el numerador es menor que el denominador. Su valor siempre es menor que la unidad (1).

• Ejemplo: $\frac{1}{2}$, $\frac{3}{5}$, $\frac{7}{10}$

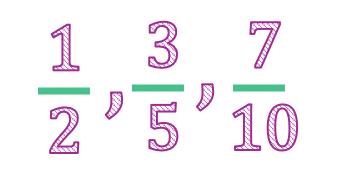
Fracciones Impropias

Una fracción es impropia cuando el numerador es igual o mayor que el denominador. Su valor es igual o mayor que la unidad (1).

• Ejemplo: $\frac{5}{3}$, $\frac{7}{7}$, $\frac{9}{4}$

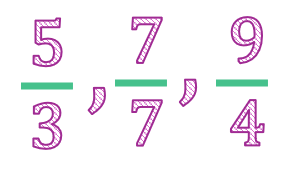
Números Mixtos o Fracciones Mixtas

Un número mixto es una combinación de un número entero y una fracción propia. Se usan para representar fracciones impropias de una manera más intuitiva.

• Ejemplo: $1\frac{2}{3}$, $2\frac{1}{4}$

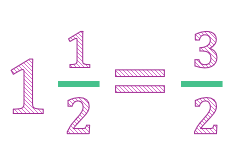
Conversión de impropias a mixtas y viceversa:

• Impropia a mixta: Divide el numerador entre el denominador. El cociente es la parte entera, el resto es el nuevo numerador y el denominador se mantiene.
  • Ejemplo: Convertir $\frac{7}{3}$ a número mixto.
    $7 \div 3 = 2$ con un resto de $1$. Así, $\frac{7}{3} = 2\frac{1}{3}$.
• Mixta a impropia: Multiplica la parte entera por el denominador y suma el numerador. El resultado es el nuevo numerador y el denominador se mantiene.
  • Ejemplo: Convertir $2\frac{1}{3}$ a fracción impropia.
    $(2 \times 3) + 1 = 6 + 1 = 7$. Así, $2\frac{1}{3} = \frac{7}{3}$.

Fracciones Equivalentes

Dos o más fracciones son equivalentes si representan la misma cantidad, aunque sus numeradores y denominadores sean diferentes. Se obtienen multiplicando o dividiendo (simplificando) el numerador y el denominador por el mismo número.

• Ejemplo: $\frac{1}{2}$, $\frac{2}{4}$, $\frac{3}{6}$ son fracciones equivalentes.
  $$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$$

Operaciones Básicas con Fracciones

Dominar las operaciones básicas con fracciones es clave para avanzar en matemáticas.

Suma y Resta de Fracciones

• Con el mismo denominador: Suma o resta los numeradores y mantén el mismo denominador.
  • Ejemplo: $\frac{3}{7} + \frac{2}{7} = \frac{3+2}{7} = \frac{5}{7}$
  • Ejemplo: $\frac{8}{9} - \frac{5}{9} = \frac{8-5}{9} = \frac{3}{9}$ (que se puede simplificar a $\frac{1}{3}$)
• Con diferente denominador: Se necesita encontrar un denominador común, generalmente el Mínimo Común Múltiplo (mcm) de los denominadores.
  1. Encuentra el mcm de los denominadores.
  2. Convierte cada fracción a una fracción equivalente con el mcm como nuevo denominador. Para ello, divide el mcm por el denominador original y multiplica el resultado por el numerador original.
  3. Suma o resta los nuevos numeradores y mantén el mcm como denominador.
  • Ejemplo: $\frac{1}{3} + \frac{1}{4}$
    • mcm(3, 4) = 12
    • $\frac{1}{3} = \frac{1 \times (12 \div 3)}{12} = \frac{1 \times 4}{12} = \frac{4}{12}$
    • $\frac{1}{4} = \frac{1 \times (12 \div 4)}{12} = \frac{1 \times 3}{12} = \frac{3}{12}$
    • $\frac{4}{12} + \frac{3}{12} = \frac{4+3}{12} = \frac{7}{12}$

Multiplicación de Fracciones

Para multiplicar fracciones, se multiplican los numeradores entre sí y los denominadores entre sí. No es necesario tener un denominador común.

• Ejemplo: $\frac{2}{3} \times \frac{4}{5} = \frac{2 \times 4}{3 \times 5} = \frac{8}{15}$

División de Fracciones

Para dividir fracciones, se multiplica la primera fracción por el inverso (o recíproco) de la segunda fracción. El inverso de una fracción se obtiene intercambiando su numerador y su denominador.

• Ejemplo: $\frac{3}{4} \div \frac{2}{5}$
  • Inverso de $\frac{2}{5}$ es $\frac{5}{2}$.
  • $\frac{3}{4} \div \frac{2}{5} = \frac{3}{4} \times \frac{5}{2} = \frac{3 \times 5}{4 \times 2} = \frac{15}{8}$

Ejercicios Resueltos de Fracciones

Aquí tienes una serie de ejercicios resueltos para practicar y afianzar tus conocimientos sobre fracciones.

Solución

Para convertir una fracción impropia a un número mixto, dividimos el numerador por el denominador.

▷ Paso 1 Realizar la división:

$$11 \div 4$$
$$11 = 4 \times 2 + 3$$
El cociente es $2$, y el resto es $3$.

▷ Paso 2 Formar el número mixto:

El cociente ($2$) es la parte entera.
El resto ($3$) es el nuevo numerador.
El denominador original ($4$) se mantiene.

Por lo tanto, $\frac{11}{4} = 2\frac{3}{4}$.

Solución

Para convertir un número mixto a una fracción impropia, multiplicamos la parte entera por el denominador y le sumamos el numerador. El denominador se mantiene.

▷ Paso 1 Multiplicar la parte entera por el denominador:

$$3 \times 2 = 6$$

▷ Paso 2 Sumar el numerador al resultado del paso anterior:

$$6 + 1 = 7$$

▷ Paso 3 Formar la fracción impropia:

El resultado del paso 2 ($7$) es el nuevo numerador.
El denominador original ($2$) se mantiene.

Por lo tanto, $3\frac{1}{2} = \frac{7}{2}$.

Solución

Para sumar fracciones con el mismo denominador, solo sumamos los numeradores y mantenemos el denominador.

▷ Paso 1 Sumar los numeradores:

$$5 + 1 = 6$$

▷ Paso 2 Mantener el denominador:

El denominador es $8$.

▷ Paso 3 Escribir el resultado y simplificar si es posible:

$$\frac{6}{8}$$

Esta fracción se puede simplificar dividiendo tanto el numerador como el denominador por su MCD, que es $2$.

$$\frac{6 \div 2}{8 \div 2} = \frac{3}{4}$$

Por lo tanto, $\frac{5}{8} + \frac{1}{8} = \frac{3}{4}$.

Solución

Para restar fracciones con el mismo denominador, restamos los numeradores y mantenemos el denominador.

▷ Paso 1 Restar los numeradores:

$$7 - 3 = 4$$

▷ Paso 2 Mantener el denominador:

El denominador es $10$.

▷ Paso 3 Escribir el resultado y simplificar si es posible:

$$\frac{4}{10}$$
Esta fracción se puede simplificar dividiendo tanto el numerador como el denominador por su MCD, que es $2$.
$$\frac{4 \div 2}{10 \div 2} = \frac{2}{5}$$

Por lo tanto, $\frac{7}{10} - \frac{3}{10} = \frac{2}{5}$.

Solución

Para sumar fracciones con diferente denominador, primero encontramos el Mínimo Común Múltiplo (mcm) de los denominadores.

▷ Paso 1 Encontrar el mcm de los denominadores (5 y 3):

$$5 = 5^1$$
$$3 = 3^1$$
$$\text{mcm}(5, 3) = 3 \times 5 = 15$$

▷ Paso 2 Convertir cada fracción a una fracción equivalente con el mcm como denominador:

Para $\frac{2}{5}$:
El denominador $5$ se multiplica por $3$ para obtener $15$. Multiplicamos el numerador por $3$ también.
$$\frac{2}{5} = \frac{2 \times 3}{5 \times 3} = \frac{6}{15}$$
Para $\frac{1}{3}$:
El denominador $3$ se multiplica por $5$ para obtener $15$. Multiplicamos el numerador por $5$ también.
$$\frac{1}{3} = \frac{1 \times 5}{3 \times 5} = \frac{5}{15}$$

▷ Paso 3 Sumar las fracciones equivalentes:

$$\frac{6}{15} + \frac{5}{15} = \frac{6+5}{15} = \frac{11}{15}$$

Por lo tanto, $\frac{2}{5} + \frac{1}{3} = \frac{11}{15}$.

Solución

Para restar fracciones con diferente denominador, primero encontramos el Mínimo Común Múltiplo (mcm) de los denominadores.

▷ Paso 1 Encontrar el mcm de los denominadores (6 y 4):

$$6 = 2 \times 3$$
$$4 = 2^2$$
$$\text{mcm}(6, 4) = 2^2 \times 3 = 4 \times 3 = 12$$

▷ Paso 2 Convertir cada fracción a una fracción equivalente con el mcm como denominador:

Para $\frac{5}{6}$:
El denominador $6$ se multiplica por $2$ para obtener $12$. Multiplicamos el numerador por $2$ también.
$$\frac{5}{6} = \frac{5 \times 2}{6 \times 2} = \frac{10}{12}$$
Para $\frac{1}{4}$:
El denominador $4$ se multiplica por $3$ para obtener $12$. Multiplicamos el numerador por $3$ también.
$$\frac{1}{4} = \frac{1 \times 3}{4 \times 3} = \frac{3}{12}$$

▷ Paso 3 Restar las fracciones equivalentes:
$$\frac{10}{12} - \frac{3}{12} = \frac{10-3}{12} = \frac{7}{12}$$

Por lo tanto, $\frac{5}{6} - \frac{1}{4} = \frac{7}{12}$.

---

Solución

Para multiplicar fracciones, multiplicamos los numeradores entre sí y los denominadores entre sí.

▷ Paso 1 Multiplicar los numeradores:
$$3 \times 2 = 6$$

▷ Paso 2 Multiplicar los denominadores:
$$7 \times 5 = 35$$

▷ Paso 3 Formar la fracción resultante:
$$\frac{6}{35}$$

Por lo tanto, $\frac{3}{7} \times \frac{2}{5} = \frac{6}{35}$.

Solución

Para dividir fracciones, multiplicamos la primera fracción por el inverso (recíproco) de la segunda fracción.

▷ Paso 1 Encontrar el inverso de la segunda fracción:
El inverso de $\frac{2}{3}$ es $\frac{3}{2}$.

▷ Paso 2 Multiplicar la primera fracción por el inverso de la segunda:
$$\frac{4}{9} \times \frac{3}{2}$$

▷ Paso 3 Multiplicar los numeradores y los denominadores:
Numeradores: $4 \times 3 = 12$
Denominadores: $9 \times 2 = 18$

▷ Paso 4 Formar la fracción resultante y simplificar si es posible:
$$\frac{12}{18}$$
Esta fracción se puede simplificar. El MCD de 12 y 18 es 6.
$$\frac{12 \div 6}{18 \div 6} = \frac{2}{3}$$

Por lo tanto, $\frac{4}{9} \div \frac{2}{3} = \frac{2}{3}$.

Solución

Para saber qué fracción del pastel se han comido en total, debemos sumar las fracciones que comió Ana y Juan.

▷ Paso 1 Identificar las fracciones a sumar:

Ana: $\frac{1}{4}$
Juan: $\frac{1}{6}$

▷ Paso 2 Encontrar el mcm de los denominadores (4 y 6):

$$4 = 2^2$$
$$6 = 2 \times 3$$
$$\text{mcm}(4, 6) = 2^2 \times 3 = 4 \times 3 = 12$$

▷ Paso 3 Convertir cada fracción a una fracción equivalente con el mcm como denominador:

Para $\frac{1}{4}$:
El denominador $4$ se multiplica por $3$ para obtener $12$. Multiplicamos el numerador por $3$ también.
$$\frac{1}{4} = \frac{1 \times 3}{4 \times 3} = \frac{3}{12}$$
Para $\frac{1}{6}$:
El denominador $6$ se multiplica por $2$ para obtener $12$. Multiplicamos el numerador por $2$ también.
$$\frac{1}{6} = \frac{1 \times 2}{6 \times 2} = \frac{2}{12}$$

▷ Paso 4 Sumar las fracciones equivalentes:

$$\frac{3}{12} + \frac{2}{12} = \frac{3+2}{12} = \frac{5}{12}$$

Respuesta: En total, se han comido $\frac{5}{12}$ del pastel.

4. Conclusión

Las fracciones son un componente esencial de las matemáticas y su comprensión es vital para la aritmética y disciplinas más avanzadas. Desde su estructura básica con numerador y denominador hasta sus clasificaciones (propias, impropias, mixtas y equivalentes), cada concepto construye una base sólida para su aplicación práctica.

Dominar las operaciones de suma, resta, multiplicación y división con fracciones te permite resolver una amplia gama de problemas, no solo en un contexto puramente matemático, sino también en situaciones cotidianas, de ingeniería o en el campo de la robótica donde las proporciones y divisiones exactas son cruciales. Con la práctica constante, estas operaciones se volverán intuitivas, abriendo la puerta a una comprensión más profunda de los números y sus relaciones.