Operaciones con Números Decimales - Ejercicios Resueltos

Los números decimales son una parte omnipresente de nuestra vida diaria. Desde calcular el costo total de la compra en el supermercado, medir ingredientes en una receta, hasta interpretar datos científicos o de ingeniería, la capacidad de realizar operaciones con ellos es una habilidad matemática fundamental. Aunque a primera vista puedan parecer más complejos que los números enteros debido a la presencia del punto decimal, las reglas para sumar, restar, multiplicar y dividir números decimales son lógicas y fáciles de dominar. 🤓

Este artículo de aritmética te guiará a través de las operaciones básicas con números decimales, proporcionando explicaciones claras y ejemplos prácticos. Dominar estas operaciones no solo es esencial para el éxito académico en matemáticas, sino que también es una herramienta indispensable para cualquier persona que necesite manejar datos cuantitativos en su vida profesional o personal. Prepárate para afianzar tus conocimientos y sentirte más seguro al trabajar con estas importantes cifras.

Trabajar con números decimales es similar a operar con números enteros, pero con especial atención a la posición del punto decimal.

Suma de Números Decimales

1. Escribe los números uno debajo del otro, alineando los puntos decimales.
2. Si es necesario, añade ceros al final de los números para que tengan la misma cantidad de cifras decimales (esto no cambia su valor).
3. Suma los números como si fueran enteros.
4. Coloca el punto decimal en el resultado, alineado con los puntos decimales de los números que sumaste.

Ejemplo: Sumar $3.25 + 1.6$.

Resta de Números Decimales

1. Escribe los números uno debajo del otro, alineando los puntos decimales.
2. Si es necesario, añade ceros al final del minuendo o sustraendo para que tengan la misma cantidad de cifras decimales.
3. Resta los números como si fueran enteros.
4. Coloca el punto decimal en el resultado, alineado con los puntos decimales de los números que restaste.

Ejemplo: Restar $7.8 - 2.35$.

Multiplicación de Números Decimales

La multiplicación de decimales no requiere alinear los puntos decimales inicialmente.

1. Multiplica los números como si fueran enteros, ignorando los puntos decimales por un momento.
2. Cuenta el número total de cifras decimales que hay entre todos los factores (los números que se multiplican).
3. En el producto (resultado de la multiplicación), coloca el punto decimal de derecha a izquierda, contando el número total de cifras decimales obtenidas en el paso anterior.

Ejemplo: Multiplicar $2.5 \times 1.3$.

$2.5$ tiene 1 cifra decimal.
$1.3$ tiene 1 cifra decimal.
Total: $1 + 1 = 2$ cifras decimales.
Colocamos el punto en 325 de derecha a izquierda 2 posiciones: $3.25$.
Por lo tanto, $2.5 \times 1.3 = 3.25$.

División de Números Decimales

La división de decimales a menudo requiere ajustar los números para trabajar con un divisor entero.

División de un Decimal por un Entero

1. Realiza la división normalmente.
2. Cuando llegues al punto decimal en el dividendo, colócalo en el cociente (el resultado).

Ejemplo: Dividir $6.4 \div 2$.

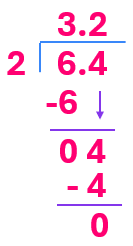
$$\begin{array}{r} 3.2 \\ 2 \overline{)6.4} \\ -6 \downarrow \\ \hline 04 \\ -4 \\ \hline 0 \end{array}$$
Por lo tanto, $6.4 \div 2 = 3.2$.

División de un Decimal por otro Decimal

1. Mueve el punto decimal del divisor hacia la derecha hasta que se convierta en un número entero.
2. Mueve el punto decimal del dividendo la misma cantidad de lugares hacia la derecha. Añade ceros si es necesario.
3. Realiza la división como si fuera la división de un decimal por un entero.

Ejemplo: Dividir $7.5 \div 0.5$.

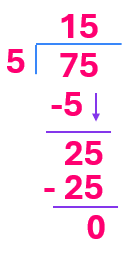
Mover el punto decimal en $0.5$ un lugar a la derecha para que sea 5.
Mover el punto decimal en $7.5$ un lugar a la derecha para que sea 75.
Ahora dividimos $75 \div 5$:
$$\begin{array}{r} 15 \\ 5 \overline{)75} \\ -5 \downarrow \\ \hline 25 \\ -25 \\ \hline 0 \end{array}$$
Por lo tanto, $7.5 \div 0.5 = 15$.

Ejercicios Resueltos

Aquí tienes una serie de ejercicios resueltos para practicar las operaciones con números decimales.

Solución

▷ Paso 1 Alinear los puntos decimales y añadir ceros si es necesario.
$$\begin{array}{r} 15.30 \\ + 7.82 \\ \hline \end{array}$$

▷ Paso 2 Sumar como si fueran enteros.
$$\begin{array}{r} 15.30 \\ + 7.82 \\ \hline 23.12 \end{array}$$

Por lo tanto, $15.3 + 7.82 = 23.12$.

Solución

▷ Paso 1 Alinear los puntos decimales y añadir ceros si es necesario.
$$\begin{array}{r} 20.50 \\ - 8.75 \\ \hline \end{array}$$

▷ Paso 2 Restar como si fueran enteros, pidiendo prestado si es necesario.
$$\begin{array}{r} 20.5^10 \\ - 8.75 \\ \hline 11.75 \end{array}$$

Por lo tanto, $20.5 - 8.75 = 11.75$.

Solución

▷ Paso 1 Multiplicar los números como si fueran enteros (42 x 31).
$$\begin{array}{r} 42 \\ \times 31 \\ \hline 42 \\ 1260 \\ \hline 1302 \end{array}$$

▷ Paso 2 Contar el total de cifras decimales en los factores.
$4.2$ tiene 1 cifra decimal.
$3.1$ tiene 1 cifra decimal.
Total de cifras decimales: $1 + 1 = 2$.

▷ Paso 3 Colocar el punto decimal en el resultado.
Contar 2 lugares desde la derecha en 1302 y colocar el punto.
$13.02$

Por lo tanto, $4.2 \times 3.1 = 13.02$.

Solución

▷ Paso 1 Multiplicar los números como si fueran enteros (5 x 12).
$$5 \times 12 = 60$$

▷ Paso 2 Contar el total de cifras decimales en los factores.
$0.05$ tiene 2 cifras decimales.
$1.2$ tiene 1 cifra decimal.
Total de cifras decimales: $2 + 1 = 3$.

▷ Paso 3 Colocar el punto decimal en el resultado.
Contar 3 lugares desde la derecha en 60. Se necesita añadir un cero a la izquierda.
$0.060$ (que es lo mismo que $0.06$).

Por lo tanto, $0.05 \times 1.2 = 0.06$.

Solución

▷ Paso 1 Realizar la división normalmente, subiendo el punto decimal al cociente.
$$\begin{array}{r} 3.2 \\ 3 \overline{)9.6} \\ -9 \downarrow \\ \hline 06 \\ -6 \\ \hline 0 \end{array}$$

Por lo tanto, $9.6 \div 3 = 3.2$.

Solución

▷ Paso 1 Mover el punto decimal en el divisor ($0.4$) un lugar a la derecha para hacerlo entero.
$0.4 \rightarrow 4$

▷ Paso 2 Mover el punto decimal en el dividendo ($12.4$) la misma cantidad de lugares a la derecha.
$12.4 \rightarrow 124$

▷ Paso 3 Realizar la división de los números enteros.
$$124 \div 4$$
$$\begin{array}{r} 31 \\ 4 \overline{)124} \\ -12 \downarrow \\ \hline 04 \\ -4 \\ \hline 0 \end{array}$$

Por lo tanto, $12.4 \div 0.4 = 31$.

Solución

▷ Paso 1 Mover el punto decimal en el divisor ($2.5$) un lugar a la derecha.
$2.5 \rightarrow 25$

▷ Paso 2 Mover el punto decimal en el dividendo ($8$) la misma cantidad de lugares a la derecha, añadiendo un cero.
$8 \rightarrow 8.0 \rightarrow 80$

▷ Paso 3 Realizar la división.
$$80 \div 25$$
$$\begin{array}{r} 3.2 \\ 25 \overline{)80.0} \\ -75 \downarrow \\ \hline 50 \\ -50 \\ \hline 0 \end{array}$$

Por lo tanto, $8 \div 2.5 = 3.2$.

Solución

Para saber cuántos trozos se obtienen, debemos dividir la longitud total de la tela por la longitud de cada trozo.

▷ Paso 1 Plantear la operación de división.
$3.75 \div 0.25$

▷ Paso 2 Mover el punto decimal en el divisor ($0.25$) dos lugares a la derecha.
$0.25 \rightarrow 25$

▷ Paso 3 Mover el punto decimal en el dividendo ($3.75$) la misma cantidad de lugares a la derecha.
$3.75 \rightarrow 375$

▷ Paso 4 Realizar la división de los números enteros.
$$375 \div 25$$
$$\begin{array}{r} 15 \\ 25 \overline{)375} \\ -25 \downarrow \\ \hline 125 \\ -125 \\ \hline 0 \end{array}$$

Respuesta: Se obtienen 15 trozos de tela.

Solución

Este problema implica una suma y una resta de números decimales.

▷ Paso 1 Calcular la cantidad de agua después de añadir.
$$150.5 + 25.75$$
Alineando puntos:
$$\begin{array}{r} 150.50 \\ + 25.75 \\ \hline 176.25 \end{array}$$
Después de añadir, hay $176.25$ litros.

▷ Paso 2 Calcular la cantidad de agua después de usar.
$$176.25 - 40.2$$
Alineando puntos:
$$\begin{array}{r} 176.25 \\ - 40.20 \\ \hline 136.05 \end{array}$$

Respuesta: Quedan $136.05$ litros de agua en el tanque.

Conclusión

Las operaciones con números decimales son una extensión natural de la aritmética básica, y su dominio es indispensable en una gran variedad de contextos, desde las finanzas personales hasta cálculos complejos en ingeniería y física. La clave para trabajar con decimales radica en entender la importancia de la posición del punto decimal, especialmente al sumar y restar, y al ajustar los números para la división.

A través de la suma y resta que exigen alineación precisa, la multiplicación que juega con el conteo de cifras decimales y la división que se beneficia de la transformación a divisores enteros, cada operación refuerza nuestra comprensión del valor posicional. Al dominar estas técnicas, no solo mejoras tu capacidad de cálculo, sino que también desarrollas una mayor precisión y confianza al interactuar con el mundo cuantitativo que te rodea. Continúa practicando, y estas operaciones se convertirán en una segunda naturaleza.