Porcentajes - Ejercicios Resueltos
¡Qué tal amigos de Fisimat! hoy hablaremos de porcentajes en el día a día, estamos rodeados de porcentajes: descuentos en tiendas, tasas de interés bancarias, estadísticas en noticias, impuestos, y mucho más. El concepto de porcentaje es una de las herramientas matemáticas más comunes y útiles, ya que nos permite expresar una parte de un total en relación con cien. Comprender qué significan y cómo se calculan los porcentajes es crucial para tomar decisiones informadas, entender información financiera y analizar datos en diversos campos. 🤓
Este artículo de aritmética e guiará a través de la definición de porcentaje, cómo se calcula y sus aplicaciones más comunes. Dominar los porcentajes no solo es fundamental para tu educación en matemáticas de secundaria y preparatoria, sino que también es una habilidad indispensable en tu vida personal y profesional, especialmente si consideras áreas como la ingeniería, la economía o incluso la robótica (donde las proporciones y eficiencias se expresan a menudo en porcentajes). Prepárate para desglosar el mundo de los porcentajes y aplicarlos con confianza.
El porcentaje es una forma de expresar una proporción o una fracción de un todo. Se basa en una relación de "tanto por ciento", es decir, de "tanto por cada cien".
El concepto de Porcentaje
El término porcentaje significa "por cada cien" o "por ciento". Se representa con el símbolo $\%$. Así, un $15\%$ significa $15$ partes de $100$ (o $\frac{15}{100}$).
Un porcentaje es esencialmente una fracción con denominador 100.
$$P\% = \frac{P}{100}$$
Ejemplo: $20\%$ es lo mismo que $\frac{20}{100}$, que simplificado es $\frac{1}{5}$, o en decimal $0.20$.
Conversiones Fundamentales
Es vital saber cómo convertir entre porcentajes, fracciones y decimales, ya que son formas equivalentes de expresar la misma cantidad.
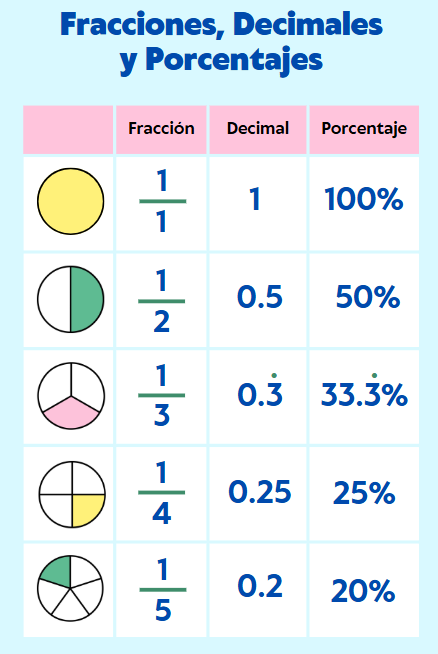
De Porcentaje a Fracción o Decimal
A fracción: Divide el número del porcentaje por 100 y simplifica la fracción.
Ejemplo: Convertir $75\%$ a fracción.
$$75\% = \frac{75}{100} = \frac{3}{4}$$
A decimal: Divide el número del porcentaje por 100 (o mueve el punto decimal dos lugares a la izquierda).
Ejemplo: Convertir $75\%$ a decimal.
$$75\% = \frac{75}{100} = 0.75$$
De Fracción a Porcentaje o Decimal
A porcentaje: Divide el numerador por el denominador y multiplica el resultado por 100.
Ejemplo: Convertir $\frac{1}{4}$ a porcentaje.
$$\frac{1}{4} = 0.25$$
$$0.25 \times 100\% = 25\%$$
A decimal: Divide el numerador por el denominador.
Ejemplo: Convertir $\frac{3}{5}$ a decimal.
$$\frac{3}{5} = 0.6$$
De Decimal a Porcentaje o Fracción
A porcentaje: Multiplica el decimal por 100 (o mueve el punto decimal dos lugares a la derecha y añade el símbolo $\%$).
Ejemplo: Convertir $0.3$ a porcentaje.
$$0.3 \times 100\% = 30\%$$
A fracción: Escribe el decimal como una fracción con denominador una potencia de 10 y simplifica.
Ejemplo: Convertir $0.125$ a fracción.
$$0.125 = \frac{125}{1000} = \frac{1}{8}$$
Aplicaciones de los Porcentajes
Los porcentajes se utilizan para resolver tres tipos principales de problemas:
Calcular el Porcentaje de una Cantidad
Para calcular un porcentaje $P\%$ de una cantidad $C$, se multiplica la cantidad $C$ por la fracción $\frac{P}{100}$ o por el decimal equivalente a $P\%$.
Fórmula: $\text{Parte} = \frac{\text{Porcentaje}}{100} \times \text{Cantidad Total}$
Ejemplo: ¿Cuál es el $15\%$ de $200$?
$$15\% \text{ de } 200 = \frac{15}{100} \times 200 = 0.15 \times 200 = 30$$
Calcular Qué Porcentaje Representa una Cantidad de un Total
Para calcular qué porcentaje representa una parte $A$ de una cantidad total $B$, se divide la parte por el total y se multiplica por 100.
Fórmula: $\text{Porcentaje} = \frac{\text{Parte}}{\text{Total}} \times 100\%$
Ejemplo: $40$ es ¿qué porcentaje de $200$?
$$\frac{40}{200} \times 100\% = 0.2 \times 100\% = 20\%$$
Calcular el Total a partir de una Parte y un Porcentaje
Para calcular la cantidad total $T$ si conocemos una parte $P$ y el porcentaje que representa esa parte ($X\%$), se divide la parte por el porcentaje en su forma decimal o fraccionaria.
Fórmula: $\text{Total} = \frac{\text{Parte}}{\text{Porcentaje}/100}$
Ejemplo: Si $30$ es el $15\%$ de un número, ¿cuál es el número?
$$\text{Número} = \frac{30}{0.15} = 200$$
Aumentos y Descuentos Porcentuales
Los porcentajes son muy comunes en cálculos de aumentos (como intereses o ganancias) y descuentos (como rebajas o pérdidas).
Aumento Porcentual
Para calcular una cantidad aumentada en un porcentaje, puedes calcular el porcentaje del aumento y sumarlo al total original, o multiplicar el total original por $(1 + \frac{\text{porcentaje}}{100})$.
Ejemplo: Un producto que cuesta $80$ aumenta su precio en un $10\%$.Aumento: $10\%$ de $80 = 0.10 \times 80 = 8$.
Nuevo precio: $80 + 8 = 88$.
O directamente: $80 \times (1 + 0.10) = 80 \times 1.10 = 88$.
Descuento Porcentual
Para calcular una cantidad con un descuento porcentual, puedes calcular el porcentaje del descuento y restarlo del total original, o multiplicar el total original por $(1 - \frac{\text{porcentaje}}{100})$.
Ejemplo: Un producto que cuesta $80$ tiene un descuento del $10\%$.
Descuento: $10\%$ de $80 = 0.10 \times 80 = 8$.
Nuevo precio: $80 - 8 = 72$.
O directamente: $80 \times (1 - 0.10) = 80 \times 0.90 = 72$.
Ejercicios Resueltos de Porcentajes
Refuerza tu comprensión de los porcentajes con esta serie de ejercicios prácticos y variados.
Problema 1. Convierte el $45\%$ a fracción irreducible y a número decimal.
Solución
▷ Paso 1 Convertir a fracción.
Un porcentaje es el número sobre 100:
$$45\% = \frac{45}{100}$$
▷ Paso 2 Simplificar la fracción.
El MCD de 45 y 100 es 5.
$$\frac{45 \div 5}{100 \div 5} = \frac{9}{20}$$
La fracción irreducible es $\frac{9}{20}$.
▷ Paso 3 Convertir a decimal.
Dividir el número del porcentaje por 100:
$$45 \div 100 = 0.45$$
El número decimal es $0.45$.
Problema 2. ¿Cuál es el $30\%$ de $150$?
Solución
▷ Paso 1 Convertir el porcentaje a decimal o fracción.
$30\% = 0.30$ o $\frac{30}{100} = \frac{3}{10}$.
▷ Paso 2 Multiplicar la cantidad total por el decimal o la fracción.
Usando decimal:
$$0.30 \times 150 = 45$$
Usando fracción:
$$\frac{3}{10} \times 150 = \frac{3 \times 150}{10} = \frac{450}{10} = 45$$
Por lo tanto, el $30\%$ de $150$ es $45$.
Problema 3. En un grupo de $60$ estudiantes, $18$ son niñas. ¿Qué porcentaje del grupo son niñas?
Solución
Para encontrar el porcentaje, dividimos la parte (número de niñas) por el total (total de estudiantes) y multiplicamos por 100.
▷ Paso 1 Plantear la división de la parte por el total.
$$\frac{18}{60}$$
▷ Paso 2 Realizar la división y convertir a decimal.
$$\frac{18}{60} = \frac{3}{10} = 0.3$$
▷ Paso 3 Multiplicar por $100\%$ para obtener el porcentaje.
$$0.3 \times 100\% = 30\%$$
Por lo tanto, el $30\%$ del grupo son niñas.
Problema 4. Si el $25\%$ de un número es $40$, ¿cuál es ese número?
Solución
Para encontrar el total, dividimos la parte conocida por el porcentaje expresado en decimal o fracción.
▷ Paso 1 Convertir el porcentaje a decimal.
$25\% = 0.25$.
▷ Paso 2 Dividir la parte por el decimal.
$$\text{Número} = \frac{40}{0.25}$$
▷ Paso 3 Realizar la división.
$$\frac{40}{0.25} = \frac{4000}{25} = 160$$
Por lo tanto, el número es $160$. (Verificación: $25\%$ de $160 = 0.25 \times 160 = 40$).
Problema 5. El precio de una camisa es 35 y tiene un descuento del $20\%$. ¿Cuál es el precio final de la camisa?
Solución
Calcularemos el descuento y luego lo restaremos del precio original.
▷ Paso 1 Calcular el monto del descuento.
Descuento = $20\%$ de $35 = 0.20 \times 35 = 7$.
▷ Paso 2 Restar el descuento del precio original.
Precio final = Precio original - Descuento
Precio final = $35 - 7 = 28$.
Alternativamente, se puede calcular el porcentaje restante a pagar: $100\% - 20\% = 80\%$.
Precio final = $80\%$ de $35 = 0.80 \times 35 = 28$.
El precio final de la camisa es $28$.
Problema 6. Un producto que costaba 120 pesos aumenta su precio un $15\%$. ¿Cuál es su nuevo precio?
Solución
Calcularemos el monto del aumento y luego lo sumaremos al precio original.
▷ Paso 1 Calcular el monto del aumento.
Aumento = $15\%$ de $120 = 0.15 \times 120 = 18$.
▷ Paso 2 Sumar el aumento al precio original.
Nuevo precio = Precio original + Aumento
Nuevo precio = $120 + 18 = 138$.
Alternativamente, se puede calcular el porcentaje total a pagar: $100\% + 15\% = 115\%$.
Nuevo precio = $115\%$ de $120 = 1.15 \times 120 = 138$.
El nuevo precio del producto es $138$.
Problema 7. En un examen de 80 preguntas, Juan respondió correctamente 68 preguntas. ¿Qué porcentaje de las preguntas respondió correctamente?
Solución
Para encontrar el porcentaje de respuestas correctas, dividimos las respuestas correctas por el total de preguntas y multiplicamos por 100.
▷ Paso 1 Plantear la división de las respuestas correctas por el total de preguntas.
$$\frac{68}{80}$$
▷ Paso 2 Realizar la división y convertir a decimal.
$$\frac{68}{80} = 0.85$$
▷ Paso 3 Multiplicar por $100\%$ para obtener el porcentaje.
$$0.85 \times 100\% = 85\%$$
Juan respondió correctamente el $85\%$ de las preguntas.
Problema 8. Una tienda ofrece un televisor con un precio original de 900. Si aplica un descuento del $15\%$ y luego un descuento adicional del $5\%$ sobre el precio ya rebajado, ¿cuál es el precio final del televisor?
Solución
Aplicaremos los descuentos de forma consecutiva.
▷ Paso 1 Calcular el precio después del primer descuento del $15\%$.
Precio después del primer descuento = $900 \times (1 - 0.15) = 900 \times 0.85 = 765$.
El precio después del primer descuento es $765$.
▷ Paso 2 Calcular el precio después del segundo descuento del $5\%$ sobre el nuevo precio.
Precio final = $765 \times (1 - 0.05) = 765 \times 0.95 = 726.75$.
El precio final del televisor es $726.75$.
Problema 9. Un capital de 5000 se invierte con una ganancia del $8\%$ anual. ¿Cuánto dinero se tendrá después de un año?
Solución
Calcularemos el aumento debido a la ganancia y lo sumaremos al capital inicial.
▷ Paso 1 Calcular el monto de la ganancia.
Ganancia = $8\%$ de $5000 = 0.08 \times 5000 = 400$.
▷ Paso 2 Sumar la ganancia al capital inicial.
Total después de un año = Capital inicial + Ganancia
Total después de un año = $5000 + 400 = 5400$.
Alternativamente:
Total después de un año = $5000 \times (1 + 0.08) = 5000 \times 1.08 = 5400$.
Después de un año, se tendrán $5400$.
Problema 10. En un recipiente hay 300 ml de una solución. Si el $40\%$ de la solución es alcohol, ¿cuántos ml de alcohol hay?
Solución
Calcularemos la cantidad de alcohol que representa el porcentaje dado.
▷ Paso 1 Convertir el porcentaje a decimal.
$40\% = 0.40$.
▷ Paso 2 Multiplicar el volumen total por el porcentaje en decimal.
Cantidad de alcohol = $0.40 \times 300 = 120$.
Hay $120$ ml de alcohol en la solución.
Problema 11. Un artículo tiene un precio de $1200$, pero se ofrece un descuento del $25%$. ¿Cuál es el precio con el descuento aplicado?
Solución
Calcularemos el monto del descuento y luego lo restaremos al precio original.
▷ Paso 1 Calcular el descuento.
Descuento = $25%$ de $1200 = 0.25 × 1200 = 300$.
▷ Paso 2 Restar el descuento al precio original.
Precio final = $1200 - 300 = 900$.
El precio con el descuento aplicado es de $900$.
Problema 12. Un automóvil ha recorrido $180$ km, lo que representa el $60%$ de un viaje. ¿Cuál es la distancia total del viaje?
Solución
Determinaremos el total usando una regla de tres simple inversa.
▷ Paso 1 Expresar el porcentaje como decimal.
$60% = 0.60$.
▷ Paso 2 Dividir la distancia recorrida entre el porcentaje.
Distancia total = $180 ÷ 0.60 = 300$.
La distancia total del viaje es de $300$ km.
Problema 13. En una clase de 40 estudiantes, el $75%$ aprobó el examen. ¿Cuántos estudiantes aprobaron?
Solución
Multiplicaremos el total de estudiantes por el porcentaje en decimal.
▷ Paso 1 Convertir el porcentaje.
$75% = 0.75$.
▷ Paso 2 Calcular cuántos aprobaron.
Estudiantes que aprobaron = $0.75 × 40 = 30$.
Aprobaron el examen $30$ estudiantes.
Problema 14. Un teléfono que costaba $10,000$ sube su precio en un $12%$. ¿Cuál es el nuevo precio?
Solución
Calcularemos el aumento y lo sumaremos al precio original.
▷ Paso 1 Calcular el incremento.
Incremento = $0.12 × 10000 = 1200$.
▷ Paso 2 Sumar el incremento al precio original.
Nuevo precio = $10000 + 1200 = 11200$.
El nuevo precio del teléfono es de $11200$.
Problema 15. Una fábrica produjo 480 unidades en un día. Si eso representa el $80%$ de su capacidad total de producción diaria, ¿cuál es la capacidad completa?
Solución
Usaremos el valor producido y el porcentaje para encontrar el total.
▷ Paso 1 Convertir el porcentaje a decimal.
$80% = 0.80$.
▷ Paso 2 Dividir el valor parcial entre el porcentaje.
Capacidad total = $480 ÷ 0.80 = 600$.
La capacidad total de producción diaria es de $600$ unidades.
Conclusión
Los porcentajes son una de las herramientas matemáticas más versátiles y de uso frecuente en nuestra vida diaria. Su concepto, que relaciona una parte con un todo sobre la base de cien, nos permite entender y expresar proporciones de manera clara y universal. Dominar las conversiones entre porcentajes, fracciones y decimales, así como las tres principales aplicaciones (calcular un porcentaje de una cantidad, qué porcentaje representa una parte de un total, y calcular el total a partir de una parte), es fundamental.
Además, la capacidad de aplicar porcentajes a aumentos y descuentos te prepara para manejar situaciones financieras y comerciales de manera efectiva. En tu rol como Ingeniero Mecatrónico y docente, y como administrador de sitios educativos, la fluidez con los porcentajes será invaluable para explicar eficiencias, crecimientos, y proporciones en física, robótica o incluso en el análisis de datos educativos. Con esta base sólida, has completado exitosamente el Nivel Básico de Aritmética, ¡felicidades!
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta
Estos temas te pueden interesar