Ángulos, Radianes y Grados - Ejercicios Resueltos
El tema de los ángulos es un tema muy importante en la geometría y herramienta esencial en la trigonometría, es por eso que el estudio de los ángulos se debe considerar como prioritario para comenzar el estudio de las matemáticas más avanzadas y la física. Desde este punto, vamos a plantear en preguntarnos. ¿qué es un ángulo? ¿cuántos ángulos conoces? ¿que tipo de ángulo se forman al analizar el andar de las manecillas del reloj a lo largo del día? ¿cuál es la importancia del estudio de los ángulos?
- Ángulos y Triángulos
- ? Elementos de la geometría
- ¿Qué es el ángulo en matemáticas?
- Equivalencias entre los sistemas circular y sexagesimal
- Ejercicios Resueltos de conversión de radianes a grados y grados a radianes
- Ejercicios para prácticar de Grados a Radianes
- Ejercicios para prácticar de Radianes a Grados
Ángulos y Triángulos
Antes de poder adentrarnos al tema de los ángulos, es importante que tengamos en cuenta algunas consideraciones, que podemos encontrar en los libros o en la red. Pero que necesitaremos tener en cuenta, para que la información sea más fácil de poder entenderla.
Algunas características de los ángulos y triángulos, son los siguientes:
Ángulos:
- Las partes de un ángulo son: el vértice y lados (semirrectas)
- Su nombre depende de la magnitud de su abertura; los ángulos igual a cero se llaman nulos, los ángulos en el intervalo (0, 90°) se llaman agudos, los ángulos igual a 90° se llaman rectos, los ángulos en el intervalo (90° a 180°) se llaman obtusos, los ángulos igual a 180° se llaman llanos, los ángulos en el intervalo (180° a 360°) se llaman oblicuos.
Triángulos:
- Están formados por tres ángulos y tres lados.
- Existen tres tipos de triángulos; Equilatero (acutángulos), isósceles (obstusángulos), escaleno (obtusángulos o acutángulos).
- Los ángulos interiores de un triángulo suman 180°
? Elementos de la geometría
Pero para comenzar, empecemos por algunos elementos básicos de la geometría, escribiendo primeramente el concepto, seguido del dibujo y su descripción.
Punto

Es la marca más diminuta que se puede dibujar, no tiene ubicación, longitud, anchura ni altura.
Recta
Puede ser la imagen de un rayo luminoso o el filo de una regla; se extiende en dos sentidos, no comienza ni termina y sus puntos conservan la misma dirección.
Plano
Es el corte más delgado posible de una superficie y puede ser una pared, un piso, etcétera.
Semirrecta
Tiene un punto de origen y se prolonga hacia el infinito en el otro extremo.
Segmento de recta
![]()
Recta cortada por dos puntos.
Paralelas
Son rectas que se desplazan en la misma dirección
Perpendiculares
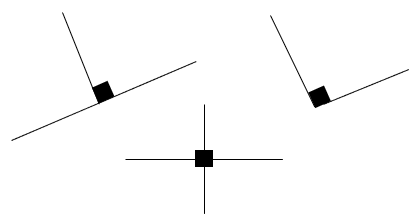
Son rectas que se cortan en un ángulo de 90°
Espacio
Estamos inmersos en él; es todo lo que nos rodea y es ilimitado.
¿Qué es el ángulo en matemáticas?
El ángulo es la abertura que se genera entre la posición inicial y posicion final de una semirrecta cuando esta gira sobre uno de sus puntos extremos llamados vértice. (tal como se ve en la imagen).
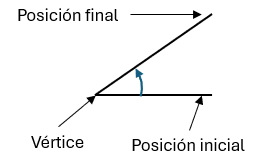
También podemos expresar de forma gráfica a los ángulos, internos o externos de esta forma:
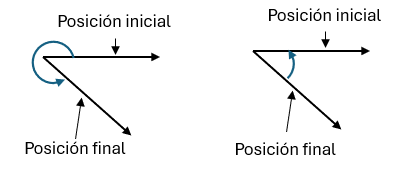
Para notar o distinguir un ángulo podemos utilizar:
Una letra mayúscula situada prácticamente en el vértice. El ángulo A.
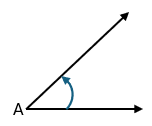
Una letra griega dentro del ángulo. El ángulo $\displaystyle \alpha $ (se lee "alfa").
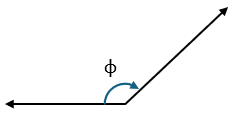
Tres letras mayúsculas, de manera que quede en medio de la letra situada en el vértice del ángulo. El ángulo ABC
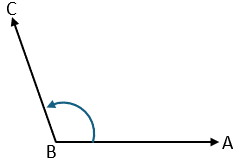
Con frecuencia, para sustituir la palabra ángulo se utiliza el símbolo , que se lee ángulo y se coloca en la testa de la letra o letras que designan el ángulo. A veces se antepone el símbolo a la letra que designa el ángulo.
El dispositivo que se ilustra a continuación se llama metrónomo y es un péndulo invertido. Si su brazo mide ?? ?? de largo y se mueve en ambos sentidos en un arco de ?? ??, calcula el ángulo ? en grados por el que pasa el péndulo en un movimiento.
- Los arcos de los ángulos se pueden medir en grados o en medidas circulares, es decir, radianes.
- Por proporcionalidad entre estas medidas se puede determinar que $\displaystyle \alpha =\frac{s}{r}$ ; sus unidades se llaman radianes.
- Como una vuelta en una circunferencia se puede medir $\displaystyle 2\pi r$ con o con $\displaystyle 360{}^\circ $, esto significa que
- Realiza la siguiente conversión $\displaystyle 1rad=\frac{{180{}^\circ }}{\pi }$ y encontrarás el ángulo que se busca, en grados. $\displaystyle 1rad=57{}^\circ 17'44.81''$

La Medida de un ángulo puede expresarse en diferentes unidades. Ahora vamos a estudiar dos sistemas de unidades de gran relevancia: el sistema sexagesimal y el sistema cíclico o circular. El sistema sexagesimal es uno de los sistemas más empleados para medir ángulos y consiste en dividir una circunferencia en 360 partes iguales llamadas grados; el grado se divide en 60 partes iguales llamadas minutos y cada minuto se divide en 60 partes iguales llamadas segundos. Los símbolos de las unidades del sistema sexagesimal se presentan en la imagen debajo.

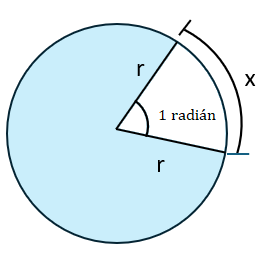
La unidad en el sistema cíclico es la unidad cíclica o unidad circular y es el ángulo central de una circunferencia cuyos lados interceptan un arco de longitud igual a la del radio.
Radián es el nombre que se le da a la unidad cíclica en este sistema. Cuando la longitud $\displaystyle s$ es igual que la de $\displaystyle r$, el ángulo $\displaystyle \alpha $ es 1 radián. (observe la imagen debajo).
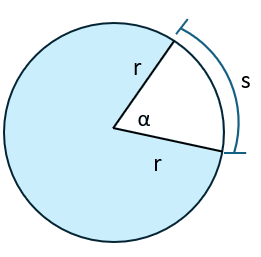
Equivalencias entre los sistemas circular y sexagesimal
Como la longitud de la circunferencia es $\displaystyle 2\pi r$ , y si representamos con $\displaystyle x$ el número de grados de un radián, podemos establecer la proporción siguiente:
$\displaystyle \frac{x}{r}=\frac{{360{}^\circ }}{{2\pi r}}$
de donde
$\displaystyle x=\frac{{360{}^\circ \cdot r}}{{2\pi r}}=\frac{{180{}^\circ }}{\pi }$
Por lo tanto, $\displaystyle x=57.28577{}^\circ $ , es decir, éste es el valor de 1 radián en grados. Sin embargo, es más fácil y práctico recordar que:
π radianes = 180°
Ejercicios Resueltos de conversión de radianes a grados y grados a radianes
Solución:
Para la conversión, vamos a multiplicar 45° por el factor $\displaystyle \frac{{\pi rad}}{{180{}^\circ }}$ , así que, esto nos quedaría:
$\displaystyle 45{}^\circ =45{}^\circ \left( {\frac{{\pi rad}}{{180{}^\circ }}} \right)=0.7854\,rad$
Solución:
$\displaystyle 58.25{}^\circ =58.25{}^\circ \left( {\frac{{\pi rad}}{{180{}^\circ }}} \right)=1.01665\,rad$
Solución:
Primero, expresemos el ángulo sólo en grados, es decir:
$\displaystyle 85{}^\circ 35'=85{}^\circ +\frac{{35{}^\circ }}{{60}}=85.5833{}^\circ $
Después, multiplicamos $\displaystyle 85.5833{}^\circ $ por el factor $\displaystyle \frac{{\pi rad}}{{180{}^\circ }}$
$\displaystyle 85.5833{}^\circ =85.5833{}^\circ \left( {\frac{{\pi rad}}{{180{}^\circ }}} \right)=1.49371\,rad$
Solución:
Procedemos de forma semejante al caso anterior, sólo que ahora el factor de conversión es $\displaystyle \frac{{180{}^\circ }}{{\pi rad}}$ así:
$\displaystyle 2.5\,rad=2.5\,rad\left( {\frac{{180{}^\circ }}{{\pi rad}}} \right)=143.23{}^\circ $
Solución:
Como en el caso anterior, tenemos que:
$\displaystyle \frac{2}{3}\,rad=\frac{2}{3}\,rad\left( {\frac{{180{}^\circ }}{{\pi rad}}} \right)=\frac{{120}}{\pi }rad=38.1971{}^\circ $
Solución:
Siguiendo el procedimiento, tenemos que:
$\displaystyle \frac{2}{3}\,rad=\frac{2}{3}\,rad\left( {\frac{{180{}^\circ }}{{\pi rad}}} \right)=120{}^\circ $
Ejercicios para prácticar de Grados a Radianes

Ejercicios para prácticar de Radianes a Grados

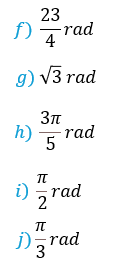
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Me interesa mucho y necesito ser una operación
1 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar