Rango, Varianza y Desviación Estándar: Medidas de Dispersión
¡Hola, amigos de Fisimat 👨🏫 Si alguna vez te has preguntado cómo los estadísticos y científicos de datos entienden la "personalidad" de un conjunto de números, estás en el lugar correcto. No basta con saber el promedio (la media), también necesitamos entender cuán dispersos o agrupados están los datos. Aquí es donde entran en juego las medidas de dispersión. En este mega artículo, vamos a desglosar tres de las más importantes: el rango, la varianza y la desviación estándar. Prepárate para un viaje fascinante que te llevará de cero a héroe en el análisis de la dispersión de datos. ¡Vamos a ello! 🚀
- ¿Por Qué Son Tan Importantes las Medidas de Dispersión?
- El Rango: La Medida Más Sencilla de Dispersión
- La Varianza: Profundizando en la Dispersión Promedio
- La Desviación Estándar: La Medida de Dispersión por Excelencia
- Ejercicios Adicionales Resueltos
- Rango vs. Varianza vs. Desviación Estándar: ¿Cuál Usar?
- Conclusión: El Poder de Ver Más Allá del Promedio
¿Por Qué Son Tan Importantes las Medidas de Dispersión?
Imagina que eres un inversor analizando dos carteras de acciones. Ambas tienen un rendimiento promedio anual del 10%. A primera vista, podrían parecer igualmente buenas. Pero, ¿y si te digo que una de ellas tuvo rendimientos anuales de 9%, 10% y 11%, mientras que la otra tuvo rendimientos de -10%, 10% y 30%? ¡La historia cambia por completo! 😱
La primera cartera es muy estable y predecible. La segunda es una montaña rusa de emociones, mucho más riesgosa. Aunque ambas tienen la misma media, su dispersión es radicalmente diferente. Las medidas de dispersión nos dan un número que cuantifica esta variabilidad. Nos ayudan a entender el riesgo, la consistencia y la homogeneidad de nuestros datos. Son herramientas esenciales en campos tan variados como las finanzas, la ingeniería, la medicina y el control de calidad industrial. Sin ellas, estaríamos navegando a ciegas, basándonos solo en promedios que pueden ser engañosos.
El Rango: La Medida Más Sencilla de Dispersión
Empecemos por la más fácil de entender y calcular: el rango. Es tan simple como parece, pero no por ello menos útil como una primera aproximación a la dispersión de tus datos.
Rango (Amplitud o Recorrido)
El rango es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. Nos da una idea rápida de la amplitud total en la que se distribuyen nuestros datos.
La fórmula no podría ser más sencilla:
\[ R = \text{Valor Máximo} - \text{Valor Mínimo} \]
El rango es excelente para obtener una visión panorámica y rápida. Sin embargo, tiene una gran debilidad: solo considera los dos valores extremos del conjunto de datos. Esto lo hace muy sensible a los valores atípicos (outliers). Un solo número extraordinariamente alto o bajo puede distorsionar por completo nuestra percepción de la dispersión.
Ejemplo 1: Cálculo del Rango en Tiempos de Carrera
Un entrenador de atletismo registra los tiempos (en segundos) de 7 corredores en una carrera de 100 metros: 10.2, 10.5, 10.1, 11.5, 10.3, 10.6, 10.4. Calculemos el rango de estos tiempos.
Solución:
Paso 1: Identificar el valor máximo y el valor mínimo.
Primero, ordenamos los datos para que sea más fácil encontrar los extremos: 10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 11.5.
- Valor Máximo = 11.5 segundos
- Valor Mínimo = 10.1 segundos
Paso 2: Aplicar la fórmula del rango.
Usamos la fórmula que aprendimos:
\[ R = 11.5 - 10.1 = 1.4 \text{ segundos} \]
El rango de los tiempos de los corredores es de 1.4 segundos. Esto nos dice que la diferencia entre el corredor más rápido y el más lento fue de 1.4 segundos. Fíjate cómo el valor de 11.5, que parece un poco más lento que el resto, tiene un gran impacto en el rango.
La Varianza: Profundizando en la Dispersión Promedio
Si el rango nos da una idea de la dispersión total, la varianza nos ofrece una medida mucho más robusta y detallada. Mide la dispersión promedio de los datos con respecto a la media. En otras palabras, nos dice qué tan lejos se encuentra cada punto de datos, en promedio, del centro del conjunto. 🧐
Varianza
La varianza es el promedio de las diferencias al cuadrado entre cada valor del conjunto de datos y la media. Elevar al cuadrado las diferencias tiene dos propósitos: primero, asegura que todas las diferencias sean positivas (evitando que las desviaciones negativas anulen a las positivas) y segundo, penaliza más a las desviaciones más grandes.
Aquí es importante hacer una distinción crucial: ¿estamos trabajando con una población (todos los miembros de un grupo) o con una muestra (un subconjunto de la población)? La fórmula cambia ligeramente.
Varianza Poblacional (\(\sigma^2\))
Se utiliza cuando tienes datos de toda la población de interés.
\[ \sigma^2 = \frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N} \]
Donde:
- \(\sigma^2\) es la varianza poblacional.
- \(N\) es el tamaño total de la población.
- \(x_i\) es cada valor individual en la población.
- \(\mu\) es la media de la población.
Varianza Muestral (\(s^2\))
Se utiliza cuando trabajas con una muestra de la población. Es la que usarás la mayor parte del tiempo en la práctica.
\[ s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1} \]
Donde:
- \(s^2\) es la varianza muestral.
- \(n\) es el tamaño de la muestra.
- \(x_i\) es cada valor individual en la muestra.
- \(\bar{x}\) es la media de la muestra.
Quizás te preguntes: ¿por qué dividimos entre \(n-1\) en la varianza muestral? 🤔 Esta pequeña modificación se conoce como la "Corrección de Bessel". Al usar la media de la muestra (\(\bar{x}\)) en lugar de la media poblacional (\(\mu\)), tendemos a subestimar ligeramente la verdadera dispersión de la población. Dividir entre \(n-1\) en lugar de \(n\) corrige este sesgo, dándonos una estimación más precisa de la varianza poblacional. ¡Un pequeño ajuste con un gran impacto teórico!
Ejemplo 2: Cálculo de la Varianza de Calificaciones
Un profesor toma una muestra de las calificaciones finales de 5 estudiantes de su clase de física: 85, 90, 75, 95, 80. Calculemos la varianza muestral de estas calificaciones.
Solución:
Paso 1: Calcular la media de la muestra (\(\bar{x}\)).
\[ \bar{x} = \frac{85 + 90 + 75 + 95 + 80}{5} = \frac{425}{5} = 85 \]
La calificación promedio es 85.
Paso 2: Calcular las diferencias al cuadrado de cada dato respecto a la media.
Ahora, para cada calificación, restamos la media y elevamos el resultado al cuadrado.
- \((85 - 85)^2 = 0^2 = 0\)
- \((90 - 85)^2 = 5^2 = 25\)
- \((75 - 85)^2 = (-10)^2 = 100\)
- \((95 - 85)^2 = 10^2 = 100\)
- \((80 - 85)^2 = (-5)^2 = 25\)
Paso 3: Sumar todas las diferencias al cuadrado.
\[ \sum (x_i - \bar{x})^2 = 0 + 25 + 100 + 100 + 25 = 250 \]
Paso 4: Aplicar la fórmula de la varianza muestral.
Dividimos la suma por \(n-1\). En este caso, \(n=5\), por lo que \(n-1=4\).
\[ s^2 = \frac{250}{4} = 62.5 \]
La varianza muestral de las calificaciones es 62.5. Este número nos da una medida de la dispersión, pero sus unidades son "puntos al cuadrado", lo cual es difícil de interpretar. Y eso nos lleva directamente a nuestra siguiente medida estrella.
La Desviación Estándar: La Medida de Dispersión por Excelencia
La desviación estándar es la reina de las medidas de dispersión. Es, con mucho, la más utilizada y citada en la estadística. ¿La razón? Resuelve el problema de interpretabilidad de la varianza.
Karl Pearson
1857-1936
Aunque el concepto de analizar las desviaciones de la media ya existía, fue el influyente matemático inglés Karl Pearson quien introdujo formalmente el término "desviación estándar" (standard deviation) en 1894. Pearson es considerado uno de los padres de la estadística matemática moderna y sus contribuciones sentaron las bases para muchas de las técnicas que usamos hoy en día.
Desviación Estándar
La desviación estándar es simplemente la raíz cuadrada de la varianza. Al tomar la raíz cuadrada, regresamos a las unidades originales de los datos, lo que hace que la desviación estándar sea mucho más fácil de interpretar que la varianza. Representa, en promedio, cuánto se desvía cada punto de datos de la media del conjunto.
Las fórmulas son una extensión directa de las de la varianza:
Desviación Estándar Poblacional (\(\sigma\))
\[ \sigma = \sqrt{\frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}} \]
Desviación Estándar Muestral (\(s\))
\[ s = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}} \]
Una desviación estándar baja indica que los puntos de datos tienden a estar muy cerca de la media (poca dispersión). Una desviación estándar alta indica que los datos están más extendidos sobre un rango de valores más amplio. Es una medida increíblemente poderosa, especialmente cuando se combina con el concepto de la distribución normal.
Regla Empírica (o Regla del 68-95-99.7)
Para datos que siguen una distribución normal (la famosa campana de Gauss), la desviación estándar tiene una propiedad maravillosa:
- Aproximadamente el 68% de los datos se encuentra dentro de una desviación estándar de la media (\(\mu \pm \sigma\)).
- Aproximadamente el 95% de los datos se encuentra dentro de dos desviaciones estándar de la media (\(\mu \pm 2\sigma\)).
- Aproximadamente el 99.7% de los datos se encuentra dentro de tres desviaciones estándar de la media (\(\mu \pm 3\sigma\)).
Esta regla nos permite visualizar rápidamente la dispersión y la probabilidad de encontrar un valor en un determinado intervalo.
Ejemplo 3: Cálculo e Interpretación de la Desviación Estándar
Continuando con el ejemplo de las calificaciones de los 5 estudiantes (85, 90, 75, 95, 80), cuya varianza muestral fue de 62.5, calculemos ahora la desviación estándar muestral.
Solución:
Paso 1: Usar el valor de la varianza ya calculado.
Ya hicimos el trabajo pesado al calcular la varianza muestral: \(s^2 = 62.5\).
Paso 2: Calcular la raíz cuadrada de la varianza.
La desviación estándar es simplemente la raíz cuadrada de este valor.
\[ s = \sqrt{s^2} = \sqrt{62.5} \approx 7.91 \]
La desviación estándar muestral es aproximadamente 7.91 puntos.
Paso 3: Interpretar el resultado.
Este es el paso clave. Tenemos una media de 85 y una desviación estándar de 7.91. Esto significa que, en promedio, las calificaciones de los estudiantes se desvían unos 7.91 puntos de la calificación promedio de 85. Nos da una medida de la consistencia de las calificaciones. Si la desviación estándar fuera, por ejemplo, de 2 puntos, significaría que las calificaciones están mucho más agrupadas alrededor de la media (un grupo de estudiantes con un rendimiento muy similar). Si fuera de 15 puntos, indicaría una gran disparidad en el rendimiento de los estudiantes.
Aquí tienes 5 ejercicios adicionales para afianzar tu conocimiento sobre las medidas de dispersión. Cada uno está diseñado para reforzar los conceptos de una manera ligeramente diferente. ¡Mucha suerte! 🤓
Ejercicios Adicionales Resueltos
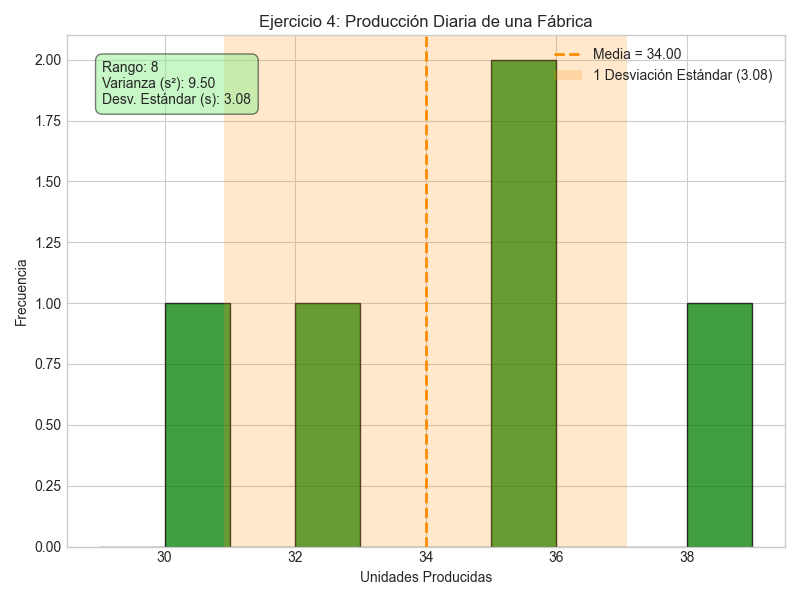
Ejemplo 4: Análisis de la Producción Diaria
Una pequeña fábrica registra el número de unidades producidas por un empleado durante una semana de trabajo (5 días). Los datos son: 30, 35, 32, 38, 35. Calcula el rango, la varianza muestral y la desviación estándar muestral para esta producción.
Solución:
Paso 1: Calcular el Rango.
Identificamos el valor máximo y mínimo.
- Valor Máximo = 38 unidades
- Valor Mínimo = 30 unidades
\[ R = 38 - 30 = 8 \text{ unidades} \]
Paso 2: Calcular la media de la muestra (\(\bar{x}\)).
\[ \bar{x} = \frac{30 + 35 + 32 + 38 + 35}{5} = \frac{170}{5} = 34 \text{ unidades} \]
Paso 3: Calcular la Varianza Muestral (\(s^2\)).
Calculamos las diferencias al cuadrado respecto a la media (34).
- \((30 - 34)^2 = (-4)^2 = 16\)
- \((35 - 34)^2 = 1^2 = 1\)
- \((32 - 34)^2 = (-2)^2 = 4\)
- \((38 - 34)^2 = 4^2 = 16\)
- \((35 - 34)^2 = 1^2 = 1\)
Sumamos estas diferencias: \( \sum (x_i - \bar{x})^2 = 16 + 1 + 4 + 16 + 1 = 38 \).
Ahora aplicamos la fórmula de la varianza muestral (\(n=5\), entonces \(n-1=4\)):
\[ s^2 = \frac{38}{4} = 9.5 \]
Paso 4: Calcular la Desviación Estándar Muestral (\(s\)).
Simplemente tomamos la raíz cuadrada de la varianza.
\[ s = \sqrt{9.5} \approx 3.08 \text{ unidades} \]
Conclusión: La producción diaria del empleado tiene una dispersión promedio de aproximadamente 3.08 unidades con respecto a su media de 34 unidades.
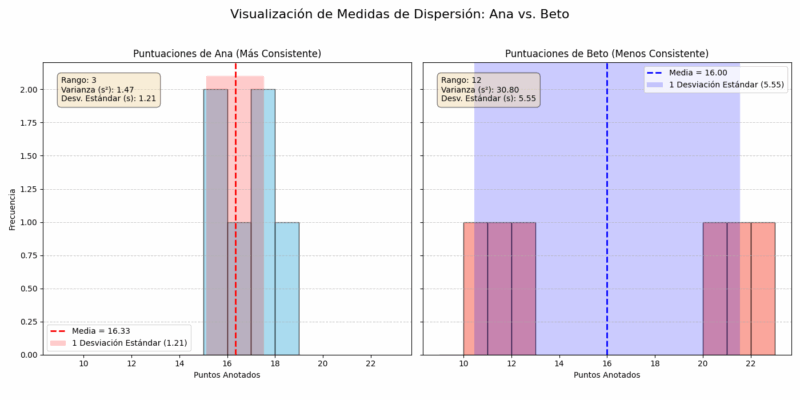
Ejemplo 5: Comparando la Consistencia de Dos Jugadores
Dos jugadores de baloncesto, Ana y Beto, han anotado los siguientes puntos en sus últimos 6 partidos:
- Ana: 15, 17, 16, 18, 15, 17
- Beto: 10, 22, 12, 20, 11, 21
Calcula la media y la desviación estándar para cada jugador y determina quién es el jugador más consistente.
Solución:
La "consistencia" en estadística se asocia con una menor dispersión. El jugador con la menor desviación estándar será el más consistente.
Análisis para Ana:
- Media de Ana (\(\bar{x}_A\)): \[ \frac{15+17+16+18+15+17}{6} = \frac{98}{6} \approx 16.33 \text{ puntos.} \]
- Varianza de Ana (\(s_A^2\)):
Suma de cuadrados de las diferencias:\[
\begin{aligned}
& (15-16.33)^2 + (17-16.33)^2 + (16-16.33)^2 + \\
& (18-16.33)^2 + (15-16.33)^2 + (17-16.33)^2 \\
& \approx 1.77 + 0.45 + 0.11 + 2.79 + 1.77 + 0.45 = 7.34
\end{aligned}
\]
Varianza: \[ s_A^2 = \frac{7.34}{6-1} = \frac{7.34}{5} = 1.468 \] - Desviación Estándar de Ana (\(s_A\)): \[ s_A = \sqrt{1.468} \approx 1.21 \text{ puntos.} \]
Análisis para Beto:
- Media de Beto (\(\bar{x}_B\)): \[ \frac{10+22+12+20+11+21}{6} = \frac{96}{6} = 16 \text{ puntos.} \]
- Varianza de Beto (\(s_B^2\)):
Suma de cuadrados de las diferencias:\[
\begin{aligned}
& (10-16)^2 + (22-16)^2 + (12-16)^2 + (20-16)^2 + \\
& (11-16)^2 + (21-16)^2 = 36 + 36 + 16 + 16 + 25 + 25 = 154
\end{aligned}
\]
Varianza: \[ s_B^2 = \frac{154}{6-1} = \frac{154}{5} = 30.8 \] - Desviación Estándar de Beto (\(s_B\)): \[ s_B = \sqrt{30.8} \approx 5.55 \text{ puntos.} \]
Conclusión: Aunque sus promedios de anotación son muy similares (16.33 vs 16), la desviación estándar de Ana (\(s_A \approx 1.21\)) es mucho menor que la de Beto (\(s_B \approx 5.55\)). Esto significa que las puntuaciones de Ana están mucho más agrupadas alrededor de su media. Por lo tanto, Ana es la jugadora más consistente.
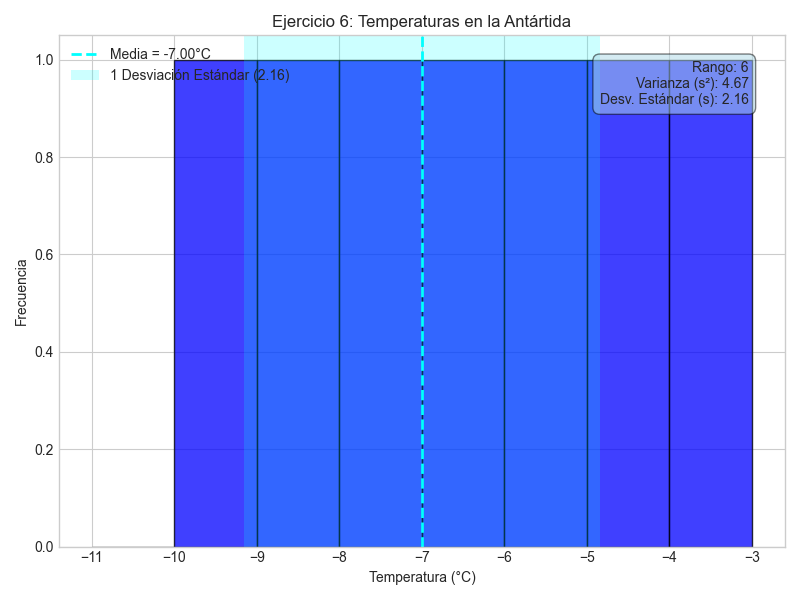
Ejemplo 6: Temperaturas bajo cero
Un científico en la Antártida registra las temperaturas diarias (en grados Celsius) durante una semana: -5, -8, -10, -7, -4, -9, -6. Calcula la desviación estándar de estas temperaturas.
Solución:
Este ejercicio muestra que los cálculos funcionan exactamente igual con números negativos.
Paso 1: Calcular la media (\(\bar{x}\)).
\[ \bar{x} = \frac{-5 + (-8) + (-10) + (-7) + (-4) + (-9) + (-6)}{7} = \frac{-49}{7} = -7^\circ\text{C} \]
Paso 2: Calcular la Varianza Muestral (\(s^2\)).
Calculamos las diferencias al cuadrado respecto a la media (-7).
- \((-5 - (-7))^2 = 2^2 = 4\)
- \((-8 - (-7))^2 = (-1)^2 = 1\)
- \((-10 - (-7))^2 = (-3)^2 = 9\)
- \((-7 - (-7))^2 = 0^2 = 0\)
- \((-4 - (-7))^2 = 3^2 = 9\)
- \((-9 - (-7))^2 = (-2)^2 = 4\)
- \((-6 - (-7))^2 = 1^2 = 1\)
Sumamos estas diferencias: \( \sum (x_i - \bar{x})^2 = 4+1+9+0+9+4+1 = 28 \).
Aplicamos la fórmula de la varianza (\(n=7\), \(n-1=6\)):
\[ s^2 = \frac{28}{6} \approx 4.67 \]
Paso 3: Calcular la Desviación Estándar Muestral (\(s\)).
\[ s = \sqrt{4.67} \approx 2.16^\circ\text{C} \]
La desviación estándar de las temperaturas es de aproximadamente 2.16 grados Celsius.
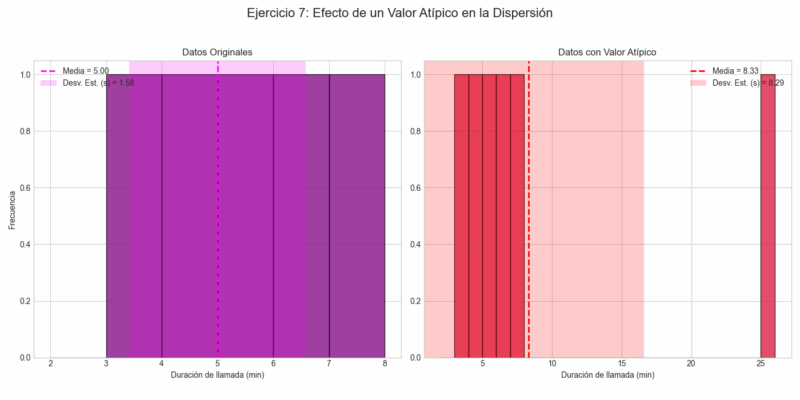
Ejemplo 7: Efecto de un Valor Atípico
Considera el siguiente conjunto de datos de la duración de 5 llamadas (en minutos): 4, 6, 5, 3, 7. Ahora, supongamos que se registra una sexta llamada que fue inusualmente larga: 25 minutos. Compara la desviación estándar antes y después de añadir este valor atípico.
Solución:
Caso 1: Datos Originales (5 llamadas)
- Media: \[ \bar{x}_1 = \frac{4+6+5+3+7}{5} = \frac{25}{5} = 5 \text{ minutos.} \]
- Suma de cuadrados de diferencias: \[ (4-5)^2 + (6-5)^2 + (5-5)^2 + (3-5)^2 + (7-5)^2 = 1+1+0+4+4 = 10 \]
- Varianza: \[ s_1^2 = \frac{10}{5-1} = 2.5 \]
- Desviación Estándar: \[ s_1 = \sqrt{2.5} \approx 1.58 \text{ minutos.} \]
Caso 2: Con el Valor Atípico (6 llamadas)
- Nuevos datos: 4, 6, 5, 3, 7, 25.
- Media: \[ \bar{x}_2 = \frac{4+6+5+3+7+25}{6} = \frac{50}{6} \approx 8.33 \text{ minutos.} \]
- Suma de cuadrados de diferencias:
\[
\begin{aligned}
& (4-8.33)^2 + (6-8.33)^2 + (5-8.33)^2 + (3-8.33)^2 + \\
& (7-8.33)^2 + (25-8.33)^2 \\
& \approx 18.75 + 5.43 + 11.09 + 28.41 + 1.77 + 277.89 = 343.34
\end{aligned}
\] - Varianza: \[ s_2^2 = \frac{343.34}{6-1} \approx 68.67 \]
- Desviación Estándar: \[ s_2 = \sqrt{68.67} \approx 8.29 \text{ minutos.} \]
Conclusión: Al añadir un solo valor atípico (25 minutos), la desviación estándar se disparó de 1.58 a 8.29. Esto demuestra potentemente cuán sensibles son la varianza y la desviación estándar a los valores extremos.
Ejemplo 8: Encontrando un Dato Faltante
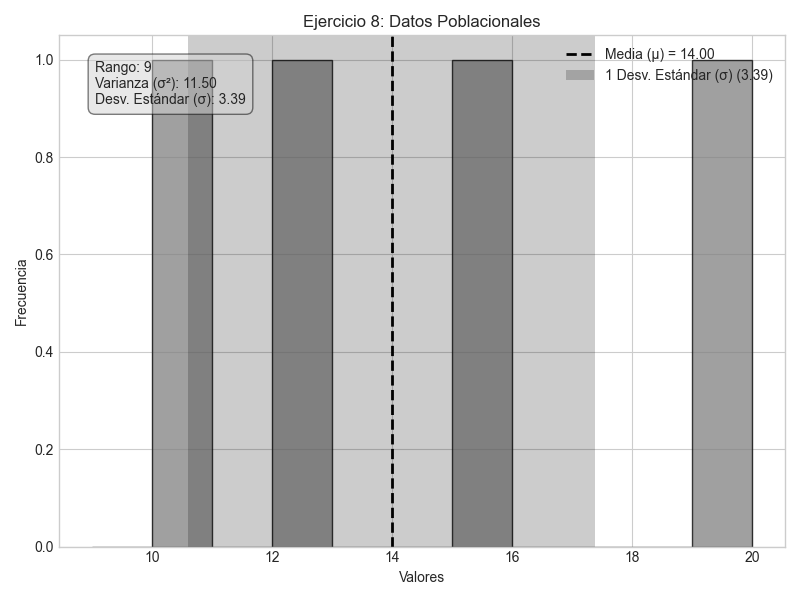
Se tiene un conjunto de cuatro números: 10, 12, 15, y \(x\). Si se sabe que la media poblacional (\(\mu\)) de este conjunto es 14, ¿cuál es el valor de la varianza poblacional (\(\sigma^2\))?
Solución:
Paso 1: Encontrar el valor de \(x\) usando la media.
La fórmula de la media poblacional es \(\mu = \frac{\sum x_i}{N}\). Conocemos \(\mu=14\) y \(N=4\).
\[ 14 = \frac{10 + 12 + 15 + x}{4} \]
\[ 14 \times 4 = 37 + x \]
\[ 56 = 37 + x \]
\[ x = 56 - 37 = 19 \]
El conjunto de datos completo es: 10, 12, 15, 19.
Paso 2: Calcular la Varianza Poblacional (\(\sigma^2\)).
Ahora que tenemos todos los datos y la media (\(\mu=14\)), usamos la fórmula de la varianza poblacional.
- \((10 - 14)^2 = (-4)^2 = 16\)
- \((12 - 14)^2 = (-2)^2 = 4\)
- \((15 - 14)^2 = 1^2 = 1\)
- \((19 - 14)^2 = 5^2 = 25\)
Sumamos estas diferencias: \( \sum (x_i - \mu)^2 = 16+4+1+25 = 46 \).
Aplicamos la fórmula de la varianza poblacional (dividimos por \(N\), no por \(N-1\)):
\[ \sigma^2 = \frac{46}{4} = 11.5 \]
La varianza poblacional del conjunto de datos es 11.5.
Rango vs. Varianza vs. Desviación Estándar: ¿Cuál Usar?
Ahora que conocemos las tres medidas, es justo preguntarse cuál es la mejor. La respuesta es: depende del contexto. Cada una tiene su lugar y su propósito.
| Medida | Ventajas | Desventajas | Cuándo Usarla |
|---|---|---|---|
| Rango | ✅ Muy fácil y rápido de calcular. Fácil de entender. | ❌ Muy sensible a valores atípicos. Ignora la distribución del resto de los datos. | Para un análisis muy preliminar, cuando la velocidad es más importante que la precisión, o en control de calidad para monitorear procesos. |
| Varianza | ✅ Utiliza todos los datos. Es fundamental en pruebas de inferencia estadística (como ANOVA). Penaliza más las desviaciones grandes. | ❌ Las unidades están al cuadrado, lo que dificulta su interpretación directa. También es sensible a valores atípicos (aunque menos que el rango). | Principalmente como un paso intermedio para calcular la desviación estándar o en procedimientos estadísticos más avanzados. |
| Desviación Estándar | 🏆 Utiliza todos los datos. Está en las mismas unidades que los datos originales, facilitando la interpretación. Es la base de muchos análisis estadísticos. | ❌ Más compleja de calcular a mano que el rango. También es sensible a valores atípicos. | Es la medida de dispersión preferida en la mayoría de los análisis estadísticos descriptivos e inferenciales. La elección por defecto para reportar la variabilidad. |
Conclusión: El Poder de Ver Más Allá del Promedio
Hemos recorrido un camino fundamental en el mundo de la estadística. Hemos aprendido que mirar solo el promedio de un conjunto de datos es como leer solo el titular de una noticia: te pierdes la mayor parte de la historia. Las medidas de dispersión como el rango, la varianza y la desviación estándar nos proporcionan el contexto, la profundidad y los detalles que necesitamos para una comprensión verdaderamente informada. 💡
El rango nos da un vistazo rápido, la varianza nos proporciona el fundamento matemático y la desviación estándar nos ofrece la medida más interpretable y universalmente aceptada de la dispersión. Entender estas herramientas no solo es crucial para aprobar un examen de estadística; es una habilidad vital para cualquiera que quiera tomar decisiones basadas en datos, ya sea en la ciencia, los negocios o incluso en la vida cotidiana. Así que la próxima vez que veas un promedio, pregunta siempre: "¿Y cuál es su desviación estándar?". Estarás un paso más cerca de pensar como un verdadero analista de datos. 💪
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar