Solución Problema 3 de Calor Específico

Con este tercer problema de Calor Específico, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de calor específico y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Problema 6.- Determine el calor específico de una pieza de 720.325 gramos que requiere 2300 calorias para elevar su temperatura de 37°C a 140°C. Consulte el cuadro de calores específicos para identificar que tipo de sustancia se trata.

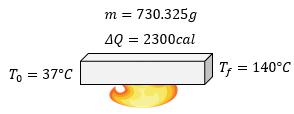
Calor Específico problema 3

Solución:

Este problema, es un problema que nos pide obtener el valor del calor específico de un material que eleva su temperatura al administrarle cierta energía de 2300 calorías. Al final debemos de demostrar que tipo de sustancia es, gracias a la tabla de calores específicos. Para poder comenzar con resolver este problema, partimos de los datos y aplicamos la fórmula.

Obtener el calor específico

Datos:

$\displaystyle m=2300g$
$\displaystyle {{T}_{0}}=37{}^\circ C$
$\displaystyle {{T}_{f}}=140{}^\circ C$
$\displaystyle \Delta Q=2300cal$

a) Obtener el calor específico del material

Recordemos que nuestra fórmula principal es la siguiente:

$\displaystyle Ce=\frac{\Delta Q}{m\Delta T}$

Vamos a sustituir los datos en la fórmula:

$\displaystyle Ce=\frac{\Delta Q}{m\Delta T}=\frac{2300cal}{\left( 720.325g \right)\left( 140{}^\circ C-37{}^\circ C \right)}$

Realizando la diferencia de temperatura:

$\displaystyle Ce=\frac{\Delta Q}{m\Delta T}=\frac{2300cal}{\left( 720.325g \right)\left( 140{}^\circ C-37{}^\circ C \right)}$

Ahora es momento de multiplicar los denoniadores.

$\displaystyle Ce=\frac{\Delta Q}{m\Delta T}=\frac{2300cal}{74193.475g{}^\circ C}$

Realizando la división:

$\displaystyle Ce=\frac{\Delta Q}{m\Delta T}=\frac{2300cal}{74193.475g{}^\circ C}=0.031\frac{cal}{g{}^\circ C}$

Obtenemos el valor de 0.031 cal/g°C , que sería nuestro calor específico.

Nota: Si buscamos nuestra tabla, el único valor de calor específico de 0.031 es para el plomo. Por lo que la pieza, que buscamos es la plata.

Respuesta:

$\displaystyle Ce=0.031\frac{cal}{{{g}^{{}^\circ }}C}$

Deja una respuesta Cancelar la respuesta