Suma y Resta de Fracciones - Ejercicios Resueltos
La suma y resta de fracciones son operaciones fundamentales en aritmética que nos permiten combinar o sustraer partes de un todo. Aunque a primera vista puedan parecer un poco más complejas que las operaciones con números enteros, su lógica es sencilla y se basa en el principio de que solo podemos sumar o restar elementos que tengan una "base" común. Imagina que intentas sumar manzanas y peras sin agruparlas por tipo: para hacerlo, necesitarías una categoría común, como "frutas". Con las fracciones, esa "base" común es el denominador.
Dominar la suma y resta de fracciones es crucial no solo para avanzar en matemáticas (álgebra, cálculo, etc.), sino también para resolver problemas cotidianos que involucran proporciones, como dividir una receta, calcular ingredientes, gestionar inventarios o interpretar datos en disciplinas como la ingeniería y la física. En este artículo, desglosaremos los métodos para sumar y restar fracciones, tanto con denominadores iguales como diferentes, y te proporcionaremos una amplia gama de ejercicios para que te conviertas en un experto.
Para sumar o restar fracciones, el requisito primordial es que tengan el mismo denominador. Si no lo tienen, debemos hacer que lo tengan.
Suma y Resta de Fracciones con el Mismo Denominador
Cuando las fracciones tienen el mismo denominador, la operación es directa y sencilla.
Suma de Fracciones con el Mismo Denominador
Para sumar fracciones con el mismo denominador:
- Mantén el mismo denominador.
- Suma los numeradores.
- Simplifica el resultado si es posible.
[alert-note]
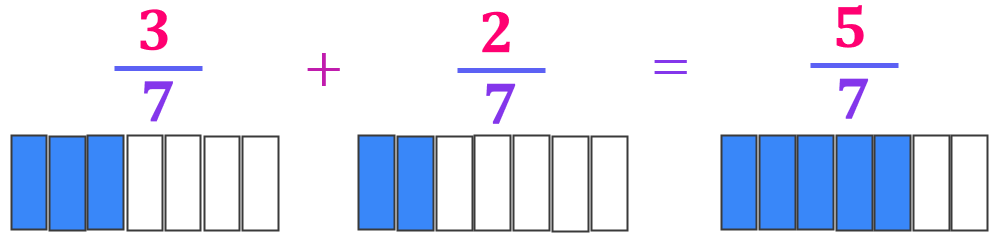
Ejemplo: Sumar $\displaystyle \frac{3}{7}+\frac{2}{7}$
[/alert-note]
Solución:
$$\frac{3}{7} + \frac{2}{7} = \frac{3+2}{7} = \frac{5}{7}$$
De forma visual, esto sería así:
Resta de Fracciones con el Mismo Denominador
Para restar fracciones con el mismo denominador:
- Mantén el mismo denominador.
- Resta los numeradores.
- Simplifica el resultado si es posible.
[alert-note]
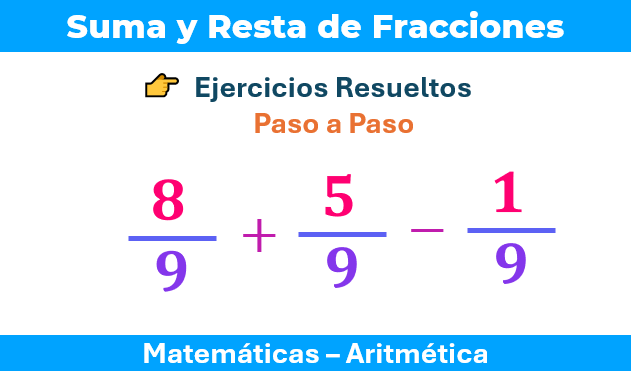
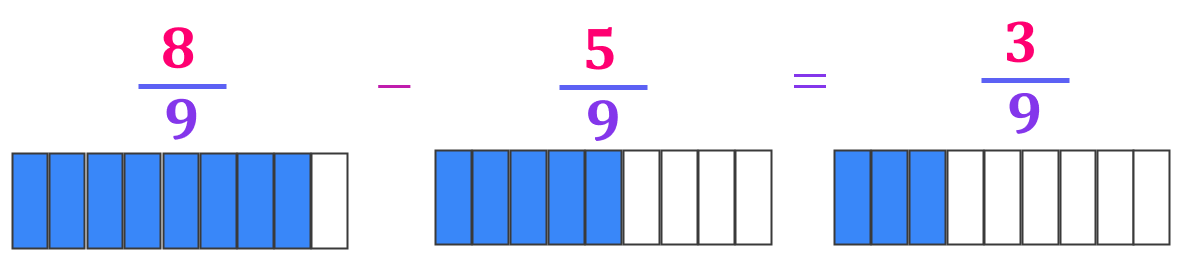
Ejemplo: Restar $\displaystyle \frac{8}{9}-\frac{5}{9}$
[/alert-note]
Solución:
$$\frac{8}{9} - \frac{5}{9} = \frac{8-5}{9} = \frac{3}{9}$$
Esta fracción se puede simplificar: $\frac{3 \div 3}{9 \div 3} = \frac{1}{3}$.
Suma y Resta de Fracciones con Diferente Denominador
Cuando las fracciones tienen denominadores diferentes, el primer paso es encontrar un denominador común, y el más eficiente es el Mínimo Común Múltiplo (mcm).
Proceso General para Denominadores Diferentes
- Encuentra el Mínimo Común Múltiplo (mcm) de todos los denominadores. Este será el nuevo denominador común.
- Convierte cada fracción original a una fracción equivalente con el mcm como nuevo denominador. Para hacer esto, divide el mcm por el denominador original y multiplica el resultado por el numerador original.
- Una vez que todas las fracciones tienen el mismo denominador (el mcm), suma o resta los numeradores, manteniendo el denominador común.
- Simplifica el resultado final si es posible.
Suma de Fracciones con Diferente Denominador
[alert-note]
Ejemplo: Sumar $\displaystyle \frac{1}{3}+\frac{1}{4}$
[/alert-note]
Solución:
- Encontrar el mcm de 3 y 4: $\text{mcm}(3, 4) = 12$.
- Convertir a fracciones equivalentes con denominador 12:
$$\frac{1}{3} = \frac{1 \times (12 \div 3)}{12} = \frac{1 \times 4}{12} = \frac{4}{12}$$
$$\frac{1}{4} = \frac{1 \times (12 \div 4)}{12} = \frac{1 \times 3}{12} = \frac{3}{12}$$ - Sumar las fracciones equivalentes:
$$\frac{4}{12} + \frac{3}{12} = \frac{4+3}{12} = \frac{7}{12}$$
Resta de Fracciones con Diferente Denominador
[alert-note]
Ejemplo: Restar $\displaystyle \frac{5}{6}-\frac{1}{4}$
[/alert-note]
Solución:
- Encontrar el mcm de 6 y 4: $\text{mcm}(6, 4) = 12$.
- Convertir a fracciones equivalentes con denominador 12:
$$\frac{5}{6} = \frac{5 \times (12 \div 6)}{12} = \frac{5 \times 2}{12} = \frac{10}{12}$$
$$\frac{1}{4} = \frac{1 \times (12 \div 4)}{12} = \frac{1 \times 3}{12} = \frac{3}{12}$$ - Restar las fracciones equivalentes:
$$\frac{10}{12} - \frac{3}{12} = \frac{10-3}{12} = \frac{7}{12}$$
📐 Método Cruzado para Sumar y Restar Fracciones
Aparte del método con el MCM, existe otro procedimiento práctico para sumar o restar fracciones con diferente denominador. Es conocido como el método cruzado, y consiste en multiplicar en cruz los numeradores por los denominadores opuestos y luego operar los resultados.
- Multiplica en cruz: el numerador de la primera fracción por el denominador de la segunda, y viceversa.
- Multiplica los denominadores entre sí para obtener el denominador común.
- Suma o resta los resultados cruzados del numerador según sea el caso.
- Simplifica el resultado si es necesario.
Ejemplo con Suma usando Método Cruzado
[alert-note]
Ejemplo: Sumar $\displaystyle \frac{1}{3}+\frac{1}{4}$ usando el método cruzado
[/alert-note]
Solución:
- Multiplicamos en cruz los numeradores por los denominadores opuestos: $$1 \times 4 = 4 \quad \text{y} \quad 1 \times 3 = 3$$
- Sumamos esos resultados: $$4 + 3 = 7$$
- Multiplicamos los denominadores entre sí: $$3 \times 4 = 12$$
- Entonces la fracción resultante es: $$\frac{7}{12}$$
Ejemplo con Resta usando Método Cruzado
[alert-note]
Ejemplo: Restar $\displaystyle \frac{5}{6}-\frac{1}{4}$ usando el método cruzado
[/alert-note]
Solución:
- Multiplicamos en cruz los numeradores: $$5 \times 4 = 20 \quad \text{y} \quad 1 \times 6 = 6$$
- Restamos: $$20 - 6 = 14$$
- Multiplicamos los denominadores: $$6 \times 4 = 24$$
- La fracción resultante es: $$\frac{14}{24}$$
- Simplificamos: $$\frac{14}{24} = \frac{7}{12}$$
Suma y Resta con Números Mixtos
Para sumar o restar números mixtos, hay dos métodos comunes:
Método 1: Convertir a Fracciones Impropias
- Convierte cada número mixto a una fracción impropia.
- Suma o resta las fracciones impropias usando los métodos explicados anteriormente (encontrando un mcm si los denominadores son diferentes).
- Convierte el resultado (si es una fracción impropia) de nuevo a un número mixto o simplifícalo.
[alert-note]
Ejemplo: Sumar $2\frac{1}{2} + 1\frac{3}{4}$.
[/alert-note]
Solución:
- Convertir a impropias:
$$2\frac{1}{2} = \frac{(2 \times 2) + 1}{2} = \frac{5}{2}$$
$$1\frac{3}{4} = \frac{(1 \times 4) + 3}{4} = \frac{7}{4}$$ - Sumar las impropias (mcm de 2 y 4 es 4):
$$\frac{5}{2} + \frac{7}{4} = \frac{5 \times 2}{4} + \frac{7}{4} = \frac{10}{4} + \frac{7}{4} = \frac{10+7}{4} = \frac{17}{4}$$ - Convertir a mixto:
$$\frac{17}{4} = 4\frac{1}{4}$$
- Convertir a impropias:
Método 2: Sumar/Restar Partes Enteras y Fraccionarias por Separado
- Suma o resta las partes enteras.
- Suma o resta las partes fraccionarias por separado (encontrando un mcm si es necesario).
- Combina los resultados. Si la suma/resta de las fracciones resulta en una fracción impropia, conviértela a mixto y suma la parte entera al total de las partes enteras.
[alert-note]
Ejemplo: Sumar $2\frac{1}{2} + 1\frac{3}{4}$.
[/alert-note]
Solución:
- Sumar partes enteras: $2 + 1 = 3$.
- Sumar partes fraccionarias: $\frac{1}{2} + \frac{3}{4}$. (mcm de 2 y 4 es 4)
$$\frac{1 \times 2}{4} + \frac{3}{4} = \frac{2}{4} + \frac{3}{4} = \frac{5}{4}$$ - Convertir la fracción impropia a mixto: $\frac{5}{4} = 1\frac{1}{4}$.
- Combinar los resultados:
$$3 + 1\frac{1}{4} = 4\frac{1}{4}$$
Ejercicios Resueltos de Suma y Resta de Fracciones
Ponte a prueba con estos ejercicios de suma y resta de fracciones.
Solución
▷ Paso 1 Sumar los numeradores, manteniendo el denominador común.
$$\frac{4}{5} + \frac{3}{5} = \frac{4+3}{5} = \frac{7}{5}$$
▷ Paso 2 Convertir la fracción impropia a número mixto.
$7 \div 5 = 1$ con resto $2$.
$$\frac{7}{5} = 1\frac{2}{5}$$
Por lo tanto, $\frac{4}{5} + \frac{3}{5} = 1\frac{2}{5}$.
Solución
▷ Paso 1 Restar los numeradores, manteniendo el denominador común.
$$\frac{11}{12} - \frac{5}{12} = \frac{11-5}{12} = \frac{6}{12}$$
▷ Paso 2 Simplificar la fracción resultante.
El MCD de 6 y 12 es 6.
$$\frac{6 \div 6}{12 \div 6} = \frac{1}{2}$$
Por lo tanto, $\frac{11}{12} - \frac{5}{12} = \frac{1}{2}$.
Solución
▷ Paso 1 Encontrar el mcm de los denominadores (2 y 5).
mcm(2, 5) = 10.
▷ Paso 2 Convertir las fracciones a equivalentes con denominador 10.
$$\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}$$
$$\frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10}$$
▷ Paso 3 Sumar las fracciones equivalentes.
$$\frac{5}{10} + \frac{4}{10} = \frac{5+4}{10} = \frac{9}{10}$$
Por lo tanto, $\frac{1}{2} + \frac{2}{5} = \frac{9}{10}$.
Solución
▷ Paso 1 Encontrar el mcm de los denominadores (8 y 4).
mcm(8, 4) = 8.
▷ Paso 2 Convertir las fracciones a equivalentes con denominador 8.
La primera fracción ya tiene denominador 8.
$$\frac{1}{4} = \frac{1 \times 2}{4 \times 2} = \frac{2}{8}$$
▷ Paso 3 Restar las fracciones equivalentes.
$$\frac{7}{8} - \frac{2}{8} = \frac{7-2}{8} = \frac{5}{8}$$
Por lo tanto, $\frac{7}{8} - \frac{1}{4} = \frac{5}{8}$.
Solución
Utilizaremos el método de sumar las partes enteras y fraccionarias por separado.
▷ Paso 1 Sumar las partes enteras.
$$1 + 2 = 3$$
▷ Paso 2 Sumar las partes fraccionarias ($\frac{1}{3} + \frac{1}{6}$).
Encontrar el mcm de 3 y 6: mcm(3, 6) = 6.
$$\frac{1}{3} = \frac{1 \times 2}{3 \times 2} = \frac{2}{6}$$
$$\frac{2}{6} + \frac{1}{6} = \frac{2+1}{6} = \frac{3}{6}$$
▷ Paso 3 Simplificar la fracción resultante del paso 2.
$$\frac{3}{6} = \frac{1}{2}$$
▷ Paso 4 Combinar la suma de las partes enteras con la fracción resultante.
$$3 + \frac{1}{2} = 3\frac{1}{2}$$
Por lo tanto, $1\frac{1}{3} + 2\frac{1}{6} = 3\frac{1}{2}$.
Solución
Utilizaremos el método de convertir a fracciones impropias.
▷ Paso 1 Convertir los números mixtos a fracciones impropias.
$$4\frac{1}{2} = \frac{(4 \times 2) + 1}{2} = \frac{9}{2}$$
$$1\frac{3}{4} = \frac{(1 \times 4) + 3}{4} = \frac{7}{4}$$
▷ Paso 2 Encontrar el mcm de los denominadores (2 y 4).
mcm(2, 4) = 4.
▷ Paso 3 Convertir las fracciones a equivalentes con denominador 4.
$$\frac{9}{2} = \frac{9 \times 2}{2 \times 2} = \frac{18}{4}$$
La segunda fracción ya tiene denominador 4: $\frac{7}{4}$.
▷ Paso 4 Restar las fracciones equivalentes.
$$\frac{18}{4} - \frac{7}{4} = \frac{18-7}{4} = \frac{11}{4}$$
▷ Paso 5 Convertir la fracción impropia a número mixto.
$11 \div 4 = 2$ con resto $3$.
$$\frac{11}{4} = 2\frac{3}{4}$$
Por lo tanto, $4\frac{1}{2} - 1\frac{3}{4} = 2\frac{3}{4}$.
Solución
▷ Paso 1 Encontrar el mcm de todos los denominadores (3, 6 y 2).
mcm(3, 6, 2) = 6.
▷ Paso 2 Convertir todas las fracciones a equivalentes con denominador 6.
$$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$$
La fracción $\frac{1}{6}$ ya tiene denominador 6.
$$\frac{1}{2} = \frac{1 \times 3}{2 \times 3} = \frac{3}{6}$$
▷ Paso 3 Realizar las operaciones con los nuevos numeradores.
$$\frac{4}{6} + \frac{1}{6} - \frac{3}{6} = \frac{4+1-3}{6} = \frac{5-3}{6} = \frac{2}{6}$$
▷ Paso 4 Simplificar el resultado.
El MCD de 2 y 6 es 2.
$$\frac{2 \div 2}{6 \div 2} = \frac{1}{3}$$
Por lo tanto, $\frac{2}{3} + \frac{1}{6} - \frac{1}{2} = \frac{1}{3}$.
Solución
Para saber cuánta harina falta, debemos restar la cantidad que ya tenemos de la cantidad necesaria.
▷ Paso 1 Plantear la operación.
$$\frac{3}{4} - \frac{1}{3}$$
▷ Paso 2 Encontrar el mcm de los denominadores (4 y 3).
mcm(4, 3) = 12.
▷ Paso 3 Convertir las fracciones a equivalentes con denominador 12.
$$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$$
$$\frac{1}{3} = \frac{1 \times 4}{3 \times 4} = \frac{4}{12}$$
▷ Paso 4 Realizar la resta.
$$\frac{9}{12} - \frac{4}{12} = \frac{9-4}{12} = \frac{5}{12}$$
Respuesta: Te faltan $\frac{5}{12}$ de taza de harina.
Solución
Para saber cuánto le falta, restamos la distancia recorrida de la distancia total. Utilizaremos el método de convertir a fracciones impropias.
▷ Paso 1 Convertir los números mixtos a fracciones impropias.
$$5\frac{1}{2} = \frac{(5 \times 2) + 1}{2} = \frac{11}{2}$$
$$2\frac{3}{4} = \frac{(2 \times 4) + 3}{4} = \frac{11}{4}$$
▷ Paso 2 Encontrar el mcm de los denominadores (2 y 4).
mcm(2, 4) = 4.
▷ Paso 3 Convertir las fracciones a equivalentes con denominador 4.
$$\frac{11}{2} = \frac{11 \times 2}{2 \times 2} = \frac{22}{4}$$
La segunda fracción ya tiene denominador 4: $\frac{11}{4}$.
▷ Paso 4 Realizar la resta.
$$\frac{22}{4} - \frac{11}{4} = \frac{22-11}{4} = \frac{11}{4}$$
▷ Paso 5 Convertir la fracción impropia a número mixto.
$11 \div 4 = 2$ con resto $3$.
$$\frac{11}{4} = 2\frac{3}{4}$$
Respuesta: Le faltan $2\frac{3}{4}$ km por recorrer.
Solución
Para encontrar la longitud total, sumaremos las longitudes de las tres secciones.
▷ Paso 1 Encontrar el mcm de los denominadores (4, 2 y 8).
Descomposición de 4: $2^2$
Descomposición de 2: $2^1$
Descomposición de 8: $2^3$
mcm(4, 2, 8) = $2^3 = 8$.
▷ Paso 2 Convertir todas las fracciones a equivalentes con denominador 8.
$$\frac{5}{4} = \frac{5 \times 2}{4 \times 2} = \frac{10}{8}$$
$$\frac{3}{2} = \frac{3 \times 4}{2 \times 4} = \frac{12}{8}$$
La fracción $\frac{7}{8}$ ya tiene denominador 8.
▷ Paso 3 Sumar las fracciones equivalentes.
$$\frac{10}{8} + \frac{12}{8} + \frac{7}{8} = \frac{10+12+7}{8} = \frac{29}{8}$$
▷ Paso 4 Convertir la fracción impropia a número mixto.
$29 \div 8 = 3$ con resto $5$.
$$\frac{29}{8} = 3\frac{5}{8}$$
Respuesta: La longitud total de la tubería es $3\frac{5}{8}$ metros.
4. Conclusión
La suma y resta de fracciones, aunque a veces intimidantes, son procesos lógicos y sistemáticos. La clave reside en la comprensión del denominador común: una vez que todas las fracciones están expresadas en las mismas "unidades" (partes iguales de un todo), las operaciones se reducen a sumar o restar sus numeradores. La práctica con fracciones con el mismo o diferente denominador, y con la inclusión de números mixtos, consolida esta habilidad fundamental.
Dominar estas operaciones no solo te equipa con herramientas esenciales para la matemática avanzada, sino que también agudiza tu pensamiento lógico y tu capacidad para resolver problemas cotidianos que involucran proporciones. En tu labor como docente, podrás transmitir esta claridad a tus alumnos, y en tu perfil de ingeniero, estas operaciones son la base para cálculos de diseño, eficiencia y análisis. ¡Sigue practicando para que la suma y resta de fracciones se conviertan en algo natural para ti!
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar