Coeficiente de Poisson - Ejercicios Resueltos
Hemos llegado al último pilar conceptual en nuestra serie introductoria sobre elasticidad. Después de entender cómo los materiales responden a fuerzas axiales (Módulo de Young), de cizalladura (Módulo de Corte) y de compresión uniforme (Módulo Volumétrico), ahora exploraremos un fenómeno fascinante y fundamental: la tendencia de los materiales a deformarse en direcciones perpendiculares a la fuerza aplicada. Esta propiedad se cuantifica mediante el Coeficiente de Poisson ($\nu$). 🤓
Introducción
Cuando estiras una banda elástica, seguramente has notado que no solo se alarga, sino que también se vuelve más delgada. De manera similar, si comprimes un borrador, se ensancha. Este efecto, donde una deformación en una dirección provoca una deformación en las direcciones perpendiculares, es un comportamiento intrínseco de la mayoría de los materiales. El Coeficiente de Poisson, nombrado en honor al matemático y físico francés Siméon Denis Poisson, es una medida adimensional que describe la magnitud de esta deformación transversal en relación con la deformación axial.

Comprender el Coeficiente de Poisson es esencial para obtener una visión tridimensional completa del comportamiento elástico de un material. Mientras que los módulos elásticos ($E, G, K$) relacionan el esfuerzo con la deformación, el Coeficiente de Poisson describe la "forma" en que ocurre esa deformación. Es crucial en aplicaciones de alta precisión donde los cambios dimensionales en todas las direcciones deben ser controlados, y como veremos, es la constante que conecta matemáticamente los tres módulos elásticos entre sí para materiales isótropos.
Definición del Coeficiente de Poisson ($\nu$)
El Coeficiente de Poisson se define a partir de la relación entre la deformación que ocurre en la dirección de la fuerza aplicada y la deformación que ocurre en las direcciones perpendiculares a ella.
Deformación Axial y Transversal
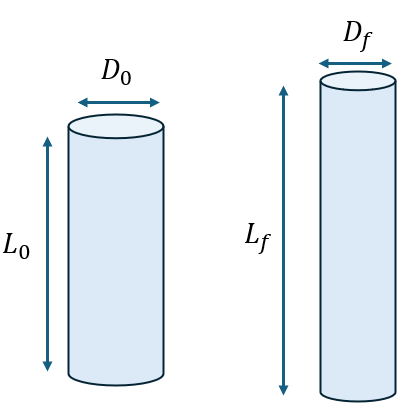
Imaginemos una barra cilíndrica de longitud inicial $L_0$ y diámetro inicial $D_0$. Si aplicamos una fuerza de tracción a lo largo de su eje:
- La barra se alargará en la dirección axial. Esta es la deformación unitaria axial ($\epsilon_{axial}$), que ya conocemos: $\epsilon_{axial} = \Delta L / L_0$.
- Simultáneamente, el diámetro de la barra disminuirá. Esta es la deformación unitaria transversal ($\epsilon_{transversal}$): $\epsilon_{transversal} = \Delta D / D_0$.
Fórmula y Convención de Signos
El Coeficiente de Poisson ($\nu$, letra griega "nu") se define como el negativo de la relación entre la deformación unitaria transversal y la deformación unitaria axial.
$$\nu = - \frac{\epsilon_{transversal}}{\epsilon_{axial}}$$
El signo negativo en la fórmula es una convención para que el Coeficiente de Poisson sea un valor positivo para la mayoría de los materiales convencionales. Analicemos por qué:
- En tracción: $\epsilon_{axial}$ es positivo (alargamiento) y $\epsilon_{transversal}$ es negativo (contracción). El cociente es negativo, y el signo menos de la fórmula lo convierte en positivo.
- En compresión: $\epsilon_{axial}$ es negativo (acortamiento) y $\epsilon_{transversal}$ es positivo (ensanchamiento). El cociente es negativo, y nuevamente, el signo menos de la fórmula lo hace positivo.
El Coeficiente de Poisson es una cantidad adimensional, ya que es la relación de dos deformaciones unitarias (que también son adimensionales).
[alert-note] Ejemplo Una varilla de $20 \text{ mm}$ de diámetro se somete a una fuerza de tracción, haciendo que su diámetro se reduzca a $19.994 \text{ mm}$. Al mismo tiempo, su longitud aumenta de $200 \text{ mm}$ a $200.4 \text{ mm}$. Calcula el Coeficiente de Poisson. [/alert-note]
Solución:
Primero, calculamos las deformaciones unitarias:
$\epsilon_{axial} = \frac{\Delta L}{L_0} = \frac{200.4 \text{ mm} - 200 \text{ mm}}{200 \text{ mm}} = \frac{0.4}{200} = 0.002$.
$\epsilon_{transversal} = \frac{\Delta D}{D_0} = \frac{19.994 \text{ mm} - 20 \text{ mm}}{20 \text{ mm}} = \frac{-0.006}{20} = -0.0003$.
Ahora, aplicamos la fórmula de $\nu$:
$\nu = - \frac{\epsilon_{transversal}}{\epsilon_{axial}} = - \frac{-0.0003}{0.002} = 0.15$.
Rango de Valores y Significado
El valor del Coeficiente de Poisson nos da información importante sobre la naturaleza de un material.
Valores Típicos para Materiales Comunes
La mayoría de los materiales de ingeniería tienen valores de $\nu$ entre $0.20$ y $0.45$.
📝 Nota: El coeficiente de Poisson \( \nu \) es una constante adimensional que varía dependiendo del tipo de material, su estado físico y condiciones específicas de temperatura y presión.
| Material | Coeficiente de Poisson \( \nu \) |
|---|---|
| Acero | \( \nu \approx 0.27 \text{–} 0.30 \) |
| Aluminio | \( \nu \approx 0.33 \) |
| Cobre | \( \nu \approx 0.34 \) |
| Titanio | \( \nu \approx 0.32 \) |
| Vidrio | \( \nu \approx 0.20 \text{–} 0.27 \) |
| Concreto | \( \nu \approx 0.10 \text{–} 0.20 \) |
| Caucho | \( \nu \approx 0.49 \text{–} 0.499 \) |
| Corcho | \( \nu \approx 0.0 \) |
| Hueso cortical | \( \nu \approx 0.30 \) |
Límites Teóricos y Casos Especiales
Para materiales isótropos estables, la teoría de la elasticidad impone límites al valor de $\nu$:
$$-1.0 < \nu \leq 0.5$$
- $\nu \approx 0.5$ (Material Incompresible): Un material con un Coeficiente de Poisson de $0.5$ no cambia su volumen total cuando se deforma elásticamente. La contracción lateral compensa perfectamente el alargamiento axial. Los cauchos y otros elastómeros se acercan mucho a este valor.
- $\nu \approx 0$ (Sin contracción lateral): Un material con un $\nu$ cercano a cero, como el corcho, se alarga sin experimentar apenas contracción en sus lados. Por esta razón, el corcho es un excelente tapón para botellas; al insertarlo, no se ensancha significativamente, evitando romper el cuello de la botella.
- $\nu < 0$ (Materiales Auxéticos): Aunque son raros, existen materiales, conocidos como auxéticos, que tienen un Coeficiente de Poisson negativo. Estos materiales se vuelven más anchos en las direcciones transversales cuando se estiran. Este comportamiento contraintuitivo se debe a su microestructura interna (a menudo con geometrías de tipo panal o reentrantes) y tiene aplicaciones especializadas en sensores, chalecos antibalas y equipos de protección.
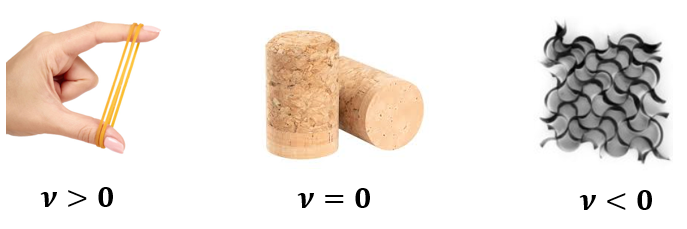
El Coeficiente de Poisson y el Cambio de Volumen
El Coeficiente de Poisson está directamente relacionado con cómo cambia el volumen de un material cuando se le somete a un esfuerzo axial. Para pequeñas deformaciones, la deformación unitaria volumétrica ($\epsilon_V$) se puede aproximar por:
$$\epsilon_V \approx \epsilon_{axial} + 2\epsilon_{transversal}$$
Sustituyendo $\epsilon_{transversal} = -\nu \epsilon_{axial}$, obtenemos:
$$\epsilon_V \approx \epsilon_{axial}(1-2\nu)$$
Esta ecuación confirma que si $\nu = 0.5$, entonces $\epsilon_V = 0$, lo que corresponde a un material incompresible (sin cambio de volumen).
[alert-note] Ejemplo Una barra de acero ($\nu=0.3$) se estira con una deformación axial de $\epsilon_{axial} = 0.001$. ¿Cuál es el cambio porcentual aproximado en su volumen?[/alert-note]
Solución:
$\epsilon_V = \epsilon_{axial}(1-2\nu) = 0.001(1 - 2 \times 0.3) = 0.001(1 - 0.6) = 0.001(0.4) = 0.0004$.
El cambio porcentual en volumen es $0.0004 \times 100\% = 0.04\%$. El volumen aumenta ligeramente.
Revisión de las Relaciones entre Módulos Elásticos
El Coeficiente de Poisson es la pieza final que conecta todos los módulos elásticos para un material isótropo. Revisemos las relaciones clave que hemos introducido a lo largo de esta serie:
- Relación entre $E$, $G$ y $\nu$:
$$E = 2G(1+\nu)$$ - Relación entre $E$, $K$ y $\nu$:
$$E = 3K(1-2\nu)$$
Estas ecuaciones demuestran que, de las cuatro constantes elásticas principales ($E, G, K, \nu$), solo dos son independientes. Si se determinan experimentalmente dos de ellas (por ejemplo, el Módulo de Young y el Coeficiente de Poisson, que son relativamente fáciles de medir), las otras dos se pueden calcular directamente.
Ejercicios Resueltos del Coeficiente de Poisson
Solución
▷ Paso 1 Calcular la deformación unitaria axial ($\epsilon_{axial}$).
$L_0 = 50 \text{ cm} = 500 \text{ mm}$.
$\Delta L = 1.2 \text{ mm}$.
$\epsilon_{axial} = \frac{\Delta L}{L_0} = \frac{1.2 \text{ mm}}{500 \text{ mm}} = 0.0024$.
▷ Paso 2 Calcular la deformación unitaria transversal ($\epsilon_{transversal}$).
$D_0 = 1.5 \text{ cm} = 15 \text{ mm}$.
$\Delta D = -0.009 \text{ mm}$ (negativo por contracción).
$\epsilon_{transversal} = \frac{\Delta D}{D_0} = \frac{-0.009 \text{ mm}}{15 \text{ mm}} = -0.0006$.
▷ Paso 3 Calcular el Coeficiente de Poisson ($\nu$).
$\nu = - \frac{\epsilon_{transversal}}{\epsilon_{axial}} = - \frac{-0.0006}{0.0024} = \frac{6}{24} = \frac{1}{4} = 0.25$.
Respuesta: El Coeficiente de Poisson del material es $0.25$.
Solución
▷ Paso 1 Identificar los datos.
$\nu = 0.33$.
$\epsilon_{axial} = -0.001$.
▷ Paso 2 Reorganizar la fórmula de $\nu$ para despejar $\epsilon_{transversal}$.
$\nu = - \frac{\epsilon_{transversal}}{\epsilon_{axial}} \Rightarrow \epsilon_{transversal} = -\nu \epsilon_{axial}$.
▷ Paso 3 Calcular $\epsilon_{transversal}$.
$\epsilon_{transversal} = -(0.33)(-0.001) = +0.00033$.
▷ Paso 4 Interpretar el resultado.
El signo positivo de $\epsilon_{transversal}$ indica que la dimensión transversal (diámetro) aumenta.
Respuesta: La deformación unitaria transversal es $+0.00033$. El diámetro de la barra aumenta.
Solución
▷ Paso 1 Calcular la deformación unitaria axial ($\epsilon_{axial}$).
Primero, calculamos $\epsilon_{axial}$ usando el Módulo de Young: $\epsilon_{axial} = \frac{\sigma}{E}$.
$\sigma = 90 \text{ MPa} = 90 \times 10^6 \text{ Pa}$.
$E = 180 \text{ GPa} = 180 \times 10^9 \text{ Pa}$.
$\epsilon_{axial} = \frac{90 \times 10^6 \text{ Pa}}{180 \times 10^9 \text{ Pa}} = \frac{1}{2000} = 0.0005$.
▷ Paso 2 Calcular la deformación unitaria transversal ($\epsilon_{transversal}$).
$\epsilon_{transversal} = -\nu \epsilon_{axial} = -(0.28)(0.0005) = -0.00014$.
▷ Paso 3 Calcular el cambio en el diámetro ($\Delta D$).
Sabemos que $\epsilon_{transversal} = \frac{\Delta D}{D_0}$, por lo tanto $\Delta D = \epsilon_{transversal} \times D_0$.
$D_0 = 2 \text{ mm}$.
$\Delta D = (-0.00014) \times (2 \text{ mm}) = -0.00028 \text{ mm}$.
Respuesta: El diámetro del alambre disminuirá en $0.00028 \text{ mm}$.
Solución
▷ Paso 1 Identificar los datos.
$G = 45 \text{ GPa}$.
$\nu = 0.34$.
▷ Paso 2 Aplicar la fórmula $E = 2G(1+\nu)$.
$E = 2 \times (45 \text{ GPa}) \times (1+0.34)$.
$E = 90 \text{ GPa} \times (1.34)$.
▷ Paso 3 Calcular el valor de $E$.
$E = 120.6 \text{ GPa}$.
Respuesta: El Módulo de Young del cobre es aproximadamente $120.6 \text{ GPa}$.
Solución
▷ Paso 1 Usar la relación $E = 3K(1-2\nu)$ para despejar $\nu$.
$\frac{E}{3K} = 1-2\nu \Rightarrow 2\nu = 1 - \frac{E}{3K} \Rightarrow \nu = \frac{1}{2} \left( 1 - \frac{E}{3K} \right)$.
▷ Paso 2 Sustituir los valores y calcular.
$\nu = \frac{1}{2} \left( 1 - \frac{190 \text{ GPa}}{3 \times 120 \text{ GPa}} \right) = \frac{1}{2} \left( 1 - \frac{190}{360} \right)$.
$\frac{190}{360} \approx 0.5277$.
$\nu = \frac{1}{2} (1 - 0.5277) = \frac{1}{2} (0.4723)$.
▷ Paso 3 Calcular el valor final de $\nu$.
$\nu \approx 0.236$.
Respuesta: El Coeficiente de Poisson del material es aproximadamente $0.236$.
Solución
▷ Paso 1 Entender la condición de incompresibilidad.
Un material incompresible mantiene su volumen constante: $V_0 = V_f$.
El volumen de un cilindro es $V = A \times L = (\pi D^2/4) \times L$.
▷ Paso 2 Establecer la ecuación de conservación del volumen.
$V_0 = V_f$
$\frac{\pi D_0^2}{4} L_0 = \frac{\pi D_f^2}{4} L_f$.
Simplificando: $D_0^2 L_0 = D_f^2 L_f$.
▷ Paso 3 Usar los datos del problema.
$D_0 = 2 \text{ cm}$.
La barra duplica su longitud, por lo tanto $L_f = 2 L_0$.
▷ Paso 4 Sustituir y despejar el diámetro final ($D_f$).
$D_0^2 L_0 = D_f^2 (2 L_0)$.
$D_0^2 = 2 D_f^2$.
$D_f^2 = \frac{D_0^2}{2}$.
$D_f = \sqrt{\frac{D_0^2}{2}} = \frac{D_0}{\sqrt{2}}$.
▷ Paso 5 Calcular el valor de $D_f$.
$D_f = \frac{2 \text{ cm}}{\sqrt{2}} \approx \frac{2 \text{ cm}}{1.414} \approx 1.414 \text{ cm}$.
Respuesta: El nuevo diámetro de la barra de caucho es aproximadamente $1.414 \text{ cm}$.
Solución
▷ Paso 1 Recordar la fórmula que relaciona $\epsilon_V$, $\epsilon_{axial}$ y $\nu$.
$\epsilon_V \approx \epsilon_{axial}(1-2\nu)$.
▷ Paso 2 Sustituir el valor de $\nu$.
$\epsilon_V \approx \epsilon_{axial}(1 - 2 \times 0.2) = \epsilon_{axial}(1 - 0.4)$.
▷ Paso 3 Calcular la relación.
$\epsilon_V \approx 0.6 \epsilon_{axial}$.
$\frac{\epsilon_V}{\epsilon_{axial}} \approx 0.6$.
Respuesta: La deformación volumétrica es aproximadamente el $60\%$ de la deformación axial para este material.
Solución
▷ Paso 1 Escribir la relación entre $E$, $K$ y $\nu$.
$E = 3K(1-2\nu)$.
▷ Paso 2
Analizar las propiedades físicas de $E$ y $K$.
El Módulo de Young ($E$) es una medida de la rigidez y se determina a partir de ensayos de tracción. Para cualquier material real que resista una fuerza, $E$ debe ser un valor positivo ($E > 0$). Un $E$ negativo implicaría que el material se alarga espontáneamente o bajo compresión, lo cual no es físicamente estable.
El Módulo Volumétrico ($K$) es una medida de la resistencia a la compresión. Un $K$ positivo significa que se necesita un aumento de presión para disminuir el volumen. Un $K$ negativo implicaría que el material se expande cuando se le comprime, lo cual violaría la estabilidad termodinámica. Por lo tanto, para un material estable, $K$ debe ser positivo ($K > 0$).
▷ Paso 3 Analizar la ecuación a la luz de estas condiciones.
Reorganizamos la ecuación: $K = \frac{E}{3(1-2\nu)}$.
Dado que hemos establecido que $K > 0$ y $E > 0$ (y el factor 3 es positivo), el denominador $3(1-2\nu)$ también debe ser positivo.
▷ Paso 4 Deducir la restricción para $\nu$.
Para que $3(1-2\nu) > 0$, se debe cumplir que $(1-2\nu) > 0$.
$1 > 2\nu$.
$\frac{1}{2} > \nu$ o $\nu < 0.5$.
Respuesta: Dado que tanto $E$ como $K$ deben ser positivos para un material físicamente estable, la relación matemática $E = 3K(1-2\nu)$ exige que el término $(1-2\nu)$ sea también positivo, lo que lleva directamente a la conclusión de que el Coeficiente de Poisson ($\nu$) debe ser menor que $0.5$.
Conclusión
El Coeficiente de Poisson ($\nu$) es la última pieza clave en nuestro estudio de las constantes elásticas fundamentales. A diferencia de los módulos, que relacionan esfuerzo y deformación, $\nu$ describe la geometría de la deformación en sí misma: la tendencia de un material a contraerse (o expandirse) lateralmente cuando se deforma axialmente. Este parámetro adimensional no solo es crucial para predecir cambios dimensionales completos en 3D, sino que también actúa como el nexo matemático que conecta el Módulo de Young, el Módulo de Corte y el Módulo Volumétrico para materiales isótropos.
Con la comprensión del Coeficiente de Poisson, hemos completado el cuadro de las propiedades que definen el comportamiento elástico lineal de los materiales. Hemos sentado una base sólida para entender cómo las fuerzas internas y los cambios dimensionales se manifiestan bajo diferentes tipos de carga. En los próximos artículos, utilizaremos estos conceptos para explorar temas más complejos y aplicados, como el análisis de la curva esfuerzo-deformación completa, los criterios de falla y aplicaciones avanzadas en ingeniería.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar