Derivada de Funciones Trigonométricas

Durante nuestro estudio del cálculo diferencial hemos aprendido que las derivadas juegan un papel muy importante para las matemáticas, la física y la química, es por ello que hemos aprendido a derivar con varios ejemplos propuestos para poder aprender de la mejor forma, las derivadas trigonométricas no deben faltar en nuestro estudio completo de derivadas.

En este artículo nos centraremos solamente a derivar funciones que impliquen funciones trigonométricas, pero haciendo uso de la práctica de las reglas de derivación algebraica, y las reglas de la derivación del producto, cociente y potencia. Para ello, nuevamente comentamos que es importante tener en cuenta algunos conceptos antes de meternos de lleno a la derivación. Por ejemplo, comprender que es el argumento en una función trascendente, y por supuesto que es una función trascendente.

Contenidos

¿Qué es una función trascendente y qué es el argumento?
Fórmulas Para las Derivadas de Funciones Trigonométricas
Derivadas Trigonométricas Resueltas

¿Qué es una función trascendente y qué es el argumento?

Las funciones trascendentes son aquellas funcionen que poseen algo llamado "argumento", dicho argumento es una cantidad numérica o simbólica que hacen que una función obtenga un valor, es decir, el argumento hace que la función se vuelva un valor numérico, sin el argumento la función se convierte en una función vacía, carece de valor.

Para citar un ejemplo, veamos la función coseno ( cos ), el coseno por si mismo no posee valor, necesita un argumento para que éste pueda tener un valor real, vamos agregarle el número 45 a su argumento, entonces tendríamos:

$\displaystyle \cos (45{}^\circ )=0.707$

Aquí vemos que el coseno, ya adquiere un valor. Entonces en conclusión, el 45 es el argumento del coseno.

Las funciones trigonométricas, logarítmicas, exponenciales e inversas son funciones trascedentes.

Lo común es que el argumento esté siempre en paréntesis después de la función principal, a veces se omite pero debemos entender cual es la función y cual el argumento.

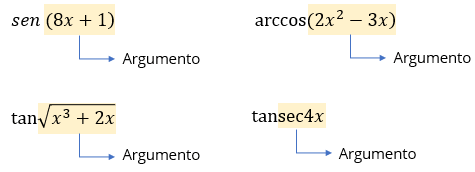
⚠️ No confundir

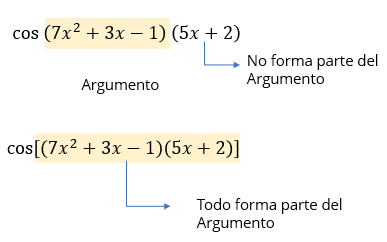
Es normal confundir el argumento con otra función si no se agrupan los términos correctamente, aquí abajo vemos un claro ejemplo del error común con los argumentos.

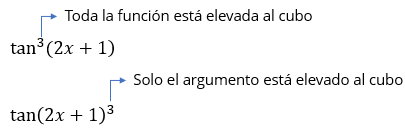
Veamos otros dos errores comunes, que el alumno puede confundir. Es mejor aclarar cuando una función está elevada a una potencia, y cuando es el argumento que está elevado a una potencia.

Teniendo en cuenta estos puntos importantes y advertencias, ahora si podemos empezar por aprender las reglas de derivación para funciones trigonométricas y posteriormente comenzar a derivar desde cero 😀

Fórmulas Para las Derivadas de Funciones Trigonométricas

$\displaystyle \frac{d}{dx}sen(u)=\cos (u)\frac{du}{dx}$

$\displaystyle \frac{d}{dx}cos(u)=-sen(u)\frac{du}{dx}$

$\displaystyle \frac{d}{dx}\tan (u)={{\sec }^{2}}(u)\frac{du}{dx}$

$\displaystyle \frac{d}{dx}cot(u)=-{{\csc }^{2}}(u)\frac{du}{dx}$

$\displaystyle \frac{d}{dx}\sec (u)=\tan (u)sec(u)\frac{du}{dx}$

$\displaystyle \frac{d}{dx}\csc (u)=-\cot (u)csc(u)\frac{du}{dx}$

Derivadas Trigonométricas Resueltas

Ejemplo 1. Resuelva la siguiente derivada

$\displaystyle y=sen(8x)$

Solución:

El argumento es 8x, por lo que podemos decir que u=8x , si aplicamos nuestra fórmula para la derivada del seno obtendremos:

$\displaystyle \frac{dy}{dx}=cos(8x)\frac{d}{dx}(8x)$

Esto es:

$\displaystyle \frac{dy}{dx}=\cos (8x)\cdot 8$

Ordenando...

Resultado:

$\displaystyle \frac{dy}{dx}=8\cos (8x)$

Ejemplo 2. Resuelva la siguiente derivada

$\displaystyle y=\cos {{x}^{3}}$

Solución:

Para este caso nuestro argumento es x³, es decir u=x³, si aplicamos nuestra formula para la derivada del coseno obtendremos:

$\displaystyle y'=-sen{{x}^{3}}\frac{d}{dx}({{x}^{3}})$

derivando x³, tenemos:

$\displaystyle y'=-sen{{x}^{3}}\left( 3{{x}^{2}} \right)$

Ordenando

Resultado:

$\displaystyle y'=-3{{x}^{2}}sen{{x}^{3}}$

Ejemplo 3. Resuelva la siguiente derivada

$\displaystyle y=\tan ({{x}^{2}}+3x-2)$

Solución:

Para este caso tenemos que el argumento es x²+3x-2 es decir u = x²+3x-2, para ello aplicamos la fórmula de la derivada de la tangente.

$\displaystyle y'={{\sec }^{2}}({{x}^{2}}+3x-2)\frac{d}{dx}\left( {{x}^{2}}+3x-2 \right)$

Esto nos daría:

$\displaystyle y'={{\sec }^{2}}({{x}^{2}}+3x-2)\left( 2x+3 \right)$

Ordenando

Resultado:

$\displaystyle y'=\left( 2x+3 \right){{\sec }^{2}}({{x}^{2}}+3x-2)$

Ejemplo 4. Resuelva la siguiente derivada

$\displaystyle y=\cot \sqrt{7x}$

Solución:

Para este caso nuestro argumento es √7x , por lo que u = √7x, para este ejemplo aplicamos la fórmula de derivada de la cotangente.

$\displaystyle y'=-{{\csc }^{2}}\sqrt{7x}\frac{d}{dx}\left( \sqrt{7x} \right)$

Pasando a la raíz cuadrada a potencia

$\displaystyle y'=-{{\csc }^{2}}\sqrt{7x}\left[ \frac{d}{dx}{{\left( 7x \right)}^{\frac{1}{2}}} \right]$

Derivamos la potencia

$\displaystyle y'=-{{\csc }^{2}}\sqrt{7x}\left[ \frac{1}{2}{{\left( 7x \right)}^{-\frac{1}{2}}}\frac{d}{dx}\left( 7x \right) \right]$

De tal forma que reduciendo obtengamos:

$\displaystyle y'=-{{\csc }^{2}}\sqrt{7x}\left[ \frac{7}{2\sqrt{7x}} \right]$

Ordenando. . .

Resultado:

$\displaystyle y'=-\frac{7}{2\sqrt{7x}}{{\csc }^{2}}\sqrt{7x}$

Ejemplo 5. Resuelva la siguiente derivada

$\displaystyle y=\sec \left( \frac{1}{{{x}^{5}}} \right)$

Solución:

Para este caso sabemos que el argumento es 1/x⁵ , es decir u = 1/x⁵ , aplicando la fórmula para la secante tenemos:

$\displaystyle \frac{dy}{dx}=\tan \left( \frac{1}{{{x}^{5}}} \right)\sec \left( \frac{1}{{{x}^{5}}} \right)\frac{d}{dx}\left( \frac{1}{{{x}^{5}}} \right)$

Antes de derivar, lo pasamos a su forma recíproca es decir 1/x⁵ es igual a x^-5

De tal forma que:

$\displaystyle \frac{dy}{dx}=\tan \left( \frac{1}{{{x}^{5}}} \right)\sec \left( \frac{1}{{{x}^{5}}} \right)\frac{d}{dx}\left( {{x}^{-5}} \right)$

Nos queda:

$\displaystyle \frac{dy}{dx}=\tan \left( \frac{1}{{{x}^{5}}} \right)\sec \left( \frac{1}{{{x}^{5}}} \right)\left[ -5{{x}^{-6}} \right]$

Por lo que. . .

$\displaystyle \frac{dy}{dx}=-5{{x}^{-6}}\tan \left( \frac{1}{{{x}^{5}}} \right)\sec \left( \frac{1}{{{x}^{5}}} \right)$

Ordenando

Resultado:

$\displaystyle \frac{dy}{dx}=-\frac{5}{{{x}^{6}}}\tan \left( \frac{1}{{{x}^{5}}} \right)\sec \left( \frac{1}{{{x}^{5}}} \right)$

Ejemplo 6. Resuelva la siguiente derivada

$\displaystyle y=\csc \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)$

Solución:

Para este caso, vemos que nuestro argumento es:

$\displaystyle u=\frac{5}{\sqrt[4]{6{{x}^{5}}-1}}$

Por lo que al aplicar la derivada de la cosecante tendremos lo siguiente:

$\displaystyle y'=-\cot \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\csc \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\frac{d}{dx}\left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)$

Vamos a pasar en potencia a la raíz de donde debemos derivar el argumento, esto para tener algo así:

$\displaystyle y'=-\cot \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\csc \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\frac{d}{dx}\left[ 5{{\left( 6{{x}^{5}}-1 \right)}^{-\frac{1}{4}}} \right]$

Ahora si podemos derivar como una potencia

$\displaystyle y'=-\cot \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\csc \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\left[ -\frac{5}{4}{{\left( 6{{x}^{5}}-1 \right)}^{-\frac{5}{4}}}\frac{d}{dx}\left( 6{{x}^{5}}-1 \right) \right]$

Luego tenemos:

Multiplicando y ordenando . . .

$\displaystyle y'=-\cot \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\csc \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\left[ -\frac{150{{x}^{4}}}{4{{\left( 6{{x}^{5}}-1 \right)}^{\frac{5}{4}}}} \right]$

Finalmente tenemos

Resultado:

$\displaystyle y'=\frac{150{{x}^{4}}}{4{{\left( 6{{x}^{5}}-1 \right)}^{\frac{5}{4}}}}\cot \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)\csc \left( \frac{5}{\sqrt[4]{6{{x}^{5}}-1}} \right)$

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

Deja una respuesta Cancelar la respuesta