Ecuación de la Elipse con Centro en el Origen

La forma de la elipse juega un papel muy importante en la Geometría Analítica, así como en la Física , principalmente en las Leyes de Kepler. En este artículo aprenderemos a resolver problemas resueltos de la ecuación de la elipse con centro en el origen.

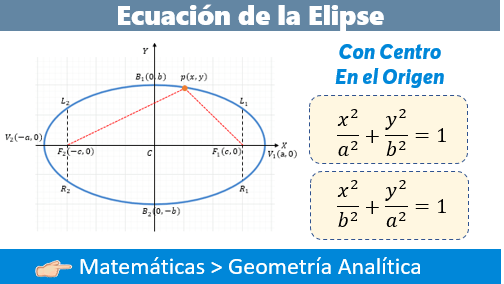
Vamos a definir a la Elipse de la siguiente manera:

La Elipse es aquél lugar geométrico que describe un punto del plano, que a su vez se mueve de tal manera que la suma de sus distancias a dos puntos fijos, llamados focos, es constante.

Contenidos

Elementos y Ecuación de la Elipse
1. 🔸 Elipse Horizontal
2. 🔸 Elipse Vertical
📃 Ejercicios Resueltos de la Ecuación de la Elipse con Centro en el Origen

Elementos y Ecuación de la Elipse

Para entender mucho mejor el tema de la elipse, vamos a conocer sus partes y elementos. La elipse la podemos encontrar de forma horizontal y de manera vertical, con pequeños cambios en sus ecuaciones finales. Comencemos con la elipse horizontal

🔸 Elipse Horizontal

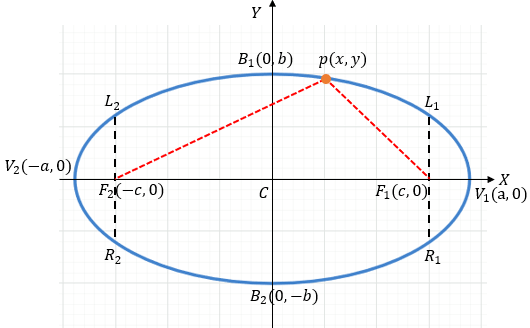
Elipse horizontal con elementos

En una parábola horizontal el eje mayor coincide con el eje "X".

Ecuación Canónica

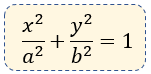
Ecuación canónica de la elipse horizontal

Elementos de la Elipse

La Elipse cuenta con Vértices, Focos, Extremos del eje menor, Extremos del eje mayor, eje focal, lado recto y excentricidad.

1️⃣ Centro:

Coordenadas (0,0).

2️⃣ Vértices:

$\displaystyle V(\pm a,0)$

3️⃣ Focos:

$\displaystyle F(\pm c,0)$

4️⃣ Extremos del eje menor:

$\displaystyle B(0,\pm b)$

5️⃣ Lado Recto:

$\displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}$

6️⃣ Excentricidad:

$\displaystyle e=\frac{c}{a}(e<1)$

7️⃣ Condición:

$\displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}$

Teniendo en cuenta que:

$\displaystyle a>b$

$\displaystyle a>c$

Dónde:

$\displaystyle b=\sqrt{{{a}^{2}}-{{c}^{2}}}$

así también:

$\displaystyle c=\sqrt{{{a}^{2}}-{{b}^{2}}}$

🔸 Elipse Vertical

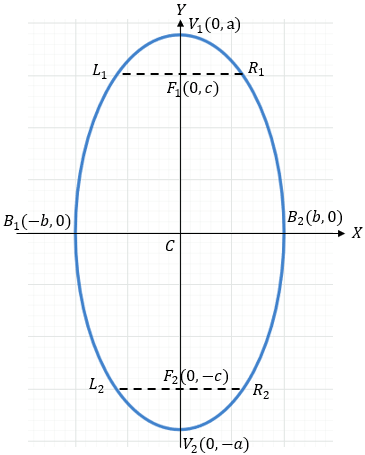
Elipse Vertical con Centro en el Origen

Ecuación Canónica

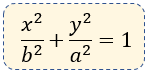
Ecuación de la Elipse Vertical

Elementos de la Elipse

La Elipse cuenta con Vértices, Focos, Extremos del eje menor, Extremos del eje mayor, eje focal, lado recto y excentricidad.

1️⃣ Centro:

Coordenadas (0,0).

2️⃣ Vértices:

$\displaystyle V(0,\pm a)$

3️⃣ Focos:

$\displaystyle F(0,\pm c)$

4️⃣ Extremos del eje menor:

$\displaystyle B(\pm b,0)$

5️⃣ Lado Recto:

$\displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}$

6️⃣ Excentricidad:

$\displaystyle e=\frac{c}{a}(e<1)$

7️⃣ Condición:

$\displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}$

Teniendo en cuenta que:

$\displaystyle a>b$

$\displaystyle a>c$

Dónde:

$\displaystyle b=\sqrt{{{a}^{2}}-{{c}^{2}}}$

así también:

$\displaystyle c=\sqrt{{{a}^{2}}-{{b}^{2}}}$

📃 Ejercicios Resueltos de la Ecuación de la Elipse con Centro en el Origen

Llegó el momento de practicar con algunos ejemplos y problemas de la elipse con centro en el origen.

Ejemplo 1. Determina los elementos y grafica la elipse, cuya ecuación es: 9x² + 4y² -36 = 0

Solución:

Vamos a mover al -36 al segundo miembro, que pasará positivo.

$\displaystyle 9{{x}^{2}}+4{{y}^{2}}=36$

Tenemos una expresión de la ecuación en su forma ordinaria, vamos a dividir todo entre 36

$\displaystyle \frac{9{{x}^{2}}+4{{y}^{2}}}{36}=\frac{36}{36}$

Esto nos daría:

$\displaystyle \frac{9{{x}^{2}}}{36}+\frac{4{{y}^{2}}}{36}=1$

Si simplificamos las divisiones, obtendremos la forma canónica de la elipse:

$\displaystyle \frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{9}=1$

En el denominador mayor "9" se encuentra justo debajo de la variable "y" , esta ecuación corresponde a una elipse vertical

Al tratarse de una elipse vertical, podemos asumir que:

$\displaystyle {{a}^{2}}=9$

$\displaystyle {{b}^{2}}=4$

Esto es porque a > b, de ahí podemos obtener:

$\displaystyle a=3$

$\displaystyle b=2$

Para obtener el valor de "c", basta con realizar el siguiente cálculo:

$\displaystyle c=\sqrt{{{a}^{2}}-{{b}^{2}}}$

Sustituyendo nuestros datos a = 3, b = 2

$\displaystyle c=\sqrt{{{(3)}^{2}}-{{(2)}^{2}}}=\sqrt{9-4}=\sqrt{5}$

Por lo que c = √5

Hasta este punto, es muy fácil encontrar los elementos de la Elipse:

💠 Obteniendo los Vértices

$\displaystyle V(0,\pm a)$

Es decir:

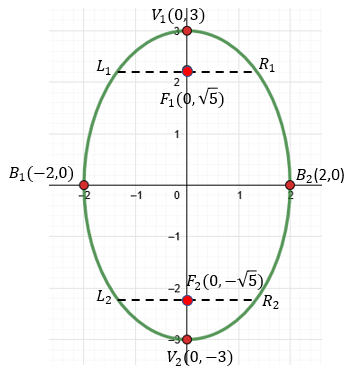
V1 (0,3) y V2 (0,-3)

💠 Obteniendo los Focos

$\displaystyle F(0,\pm c)$

Es decir:

F1 (0, √5) y F2 (0, -√5)

💠 Extremos del Eje menor

$\displaystyle B(\pm b,0)$

Es decir:

B1 (2, 0) y B2 (-2,0)

💠 Obteniendo el Lado Recto

$\displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}=\frac{2{{(2)}^{2}}}{3}=\frac{8}{3}$

💠 Excentricidad

$\displaystyle e=\frac{c}{a}=\frac{\sqrt{5}}{3}=0.745$

💠 Gráfica de la Elipse Vertical

Elipse Vertical ejercicios

Ejemplo 2. Determina los elementos y grafica la elipse, cuya ecuación es: 16x² + 25y² - 400= 0

Solución:

Vamos a mover al -400 al segundo miembro, que lógicamente pasará positivo.

$\displaystyle 16{{x}^{2}}+25{{y}^{2}}=400$

Tenemos una expresión de la ecuación en su forma ordinaria, vamos a dividir la igualdad entre 400.

$\displaystyle \frac{16{{x}^{2}}+25{{y}^{2}}}{400}=\frac{400}{400}$

Esto nos daría:

$\displaystyle \frac{16{{x}^{2}}}{400}+\frac{25{{y}^{2}}}{400}=1$

Simplificando las divisiones del primer miembro, obtendremos la forma canónica de la elipse:

$\displaystyle \frac{{{x}^{2}}}{25}+\frac{{{y}^{2}}}{16}=1$

En el denominador mayor "25" se encuentra justo debajo de la variable "x", esta ecuación corresponde a una elipse horizontal

Al tratarse de una elipse horizontal, podemos asumir que:

$\displaystyle {{a}^{2}}=25$

$\displaystyle {{b}^{2}}=16$

Obteniendo la raíz cuadrada de "a" y "b", obtenemos:

$\displaystyle a=5$

$\displaystyle b=4$

Para obtener el valor de "c" , basta con realizar el siguiente cálculo:

$\displaystyle c=\sqrt{{{a}^{2}}-{{b}^{2}}}=\sqrt{{{(5)}^{2}}-{{(4)}^{2}}}=\sqrt{25-16}=\sqrt{9}=3$

Por lo que c = 3

Teniendo en cuenta estos puntos, es muy fácil obtener los elementos de la Elipse.

💠 Obteniendo los Vértices

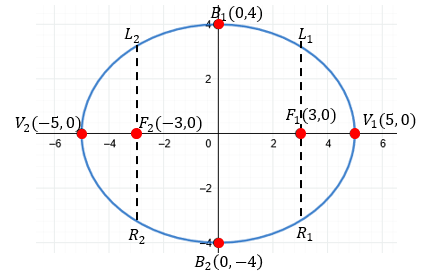
V1 (5, 0) y V2 (-5, 0)

💠 Obteniendo los Focos

F1 (3, 0) y F2 (-3, 0)

💠 Extremos del eje menor

B1 (0, 4) y B2 (0, -4)

💠 Obteniendo el Lado Recto

$\displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}=\frac{2{{(4)}^{2}}}{5}=\frac{32}{5}$

💠 Excentricidad

$\displaystyle e=\frac{c}{a}=\frac{3}{5}=0.6$

💠 Gráfica de la Elipse Horizontal

Elipse Horizontal

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

19 Comentarios Publicados

Abraham dice:

24 mayo, 2020 a las 3:08 pm

Demasiado agradecido, Dios lo bendiga!

Responder
Edinson Puente dice:

7 diciembre, 2020 a las 6:51 pm

Excelente clase, felicitaciones y que Dios los bendiga.

Responder
1. Carlos julián dice:
  
  8 diciembre, 2020 a las 6:26 am
  
  Muchas gracias Edinson por tu comentario, estamos trabajando duro para dar más ejercicios resueltos.
  
  Responder
Emilio dice:

8 enero, 2021 a las 3:38 pm

falto mencionar la ecuación general de la elipse

Responder
Luisa Esquivel dice:

14 mayo, 2021 a las 1:49 pm

Esta muy bien explicado, me ayudo mucho 😀

Responder
Luisa Esquivel dice:

14 mayo, 2021 a las 1:50 pm

Esta muy bien explicado, me ayudo mucho 😀

Responder
Jose Tovar dice:

4 junio, 2021 a las 4:12 pm

Bien, agradecido por la explicación, fue suficiente

Responder
1. Carlos julián dice:
  
  5 junio, 2021 a las 8:52 am
  
  Gracias José!
  
  Responder
Betty dice:

11 agosto, 2021 a las 3:00 pm

Gracias, que bien explicado esta el proceso, a ver si hayo la elipse con centro en (h,k)

Responder
1. Carlos julián dice:
  
  13 agosto, 2021 a las 9:51 am
  
  Gracias Betty
  
  Responder
Johanna dice:

29 octubre, 2021 a las 9:26 pm

esta información me ayudará más adelante, gracias !

Responder
1. Carlos julián dice:
  
  31 octubre, 2021 a las 7:08 am
  
  Muchas gracias Johanna!
  
  Responder
Johanna dice:

4 noviembre, 2021 a las 9:54 pm

buena información, me ayudo!

Responder
Juan Luis Rodríguez de Luna dice:

16 noviembre, 2021 a las 9:00 pm

Felicidades el articulo muy bien explicado. Gracias es de bastante utilidad.

Responder
profe naza dice:

11 junio, 2022 a las 9:08 pm

siempre , siempre , siempre excelente explicación ; para estudiantes y para profes ... cordial saludo desde la capital de la salsa Cali - Colombia

Responder
1. Carlos julián dice:
  
  14 junio, 2022 a las 11:01 am
  
  Gracias!
  
  Responder
Jimena dice:

24 septiembre, 2023 a las 3:36 pm

Excelente 👌

Responder
Jimena dice:

24 septiembre, 2023 a las 3:37 pm

Excelente 👌 explicación 👍 bn aprendizaje 👍

Responder
Francisco Guzmán dice:

20 febrero, 2024 a las 6:28 pm

Muy bien explicado los ejercicio, lo felicito. Saludos.

Responder

Deja una respuesta Cancelar la respuesta