Ecuación de la Hipérbola con Centro fuera del Origen

El estudio de la Hipérbola es la última forma geométrica que podemos encontrar en la Geometría Analítica. En este artículo hablaremos sobre la hipérbola con centro fuera del origen. Pero es recomendable analizar el tema de la hipérbola con centro en el origen. Ya que poseen lo mismos elementos, pero varían en las ecuaciones.

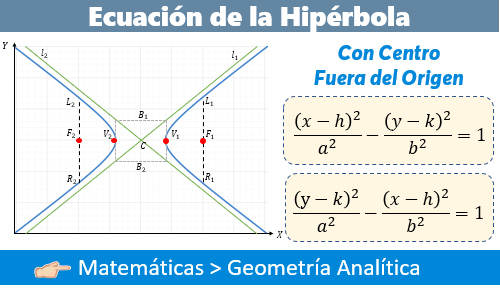
Ecuación de la Hipérbola con centro fuera del origen

Contenidos

🔱 Ecuación y Elementos de la Hipérbola
📃 Ejercicios Resueltos de la Ecuación de la Hipérbola con Centro fuera del Origen

🔱 Ecuación y Elementos de la Hipérbola

Los elementos más importantes en una hipérbola son los vértices, focos, extremos del eje conjugado y las ecuaciones de las asíntotas. Así también el centro que estará indicado por las coordenadas (h, k).

🔹 Hipérbola Horizontal con Centro en (h, k)

La ecuación particular de dicha hipérbola es la siguiente:

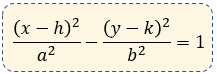
Ecuación de la hipérbola horizontal

Si el eje focal es horizontal.

Elementos

1️⃣ Vértice:

$\displaystyle V(h\pm a,k)$

2️⃣ Focos:

$\displaystyle F(h\pm c,k)$

3️⃣ Extremos del eje conjugado:

$\displaystyle B(h,k\pm b)$

4️⃣ Ecuaciones de las asíntotas:

$\displaystyle {{l}_{1}}:y-k=\frac{b}{a}\left( x-h \right)$

$\displaystyle {{l}_{2}}:y-k=-\frac{b}{a}\left( x-h \right)$

🔹 Hipérbola Vertical con Centro en (h, k)

La ecuación particular de dicha hipérbola es la siguiente:

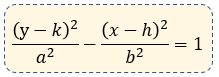
Ecuación de la hipérbola vertical

Si el eje focal es vertical.

Elementos

1️⃣ Vértice:

$\displaystyle V(h,k\pm a)$

2️⃣ Focos:

$\displaystyle F(h,k\pm c)$

3️⃣ Extremos del eje conjugado:

$\displaystyle B(h\pm b,k)$

4️⃣ Ecuaciones de las asíntotas:

$\displaystyle {{l}_{1}}:y-k=\frac{a}{b}\left( x-h \right)$

$\displaystyle {{l}_{2}}:y-k=-\frac{a}{b}\left( x-h \right)$

Ecuación general de la Hipérbola:

La ecuación general de la hipérbola es la siguiente:

$\displaystyle A{{x}^{2}}+C{{y}^{2}}+Dx+Ey+F=0$

Con A y C de signo contrario.

📃 Ejercicios Resueltos de la Ecuación de la Hipérbola con Centro fuera del Origen

Veamos algunos ejemplos de la ecuación de la hipérbola.

Ejemplo 1. Determine los elementos de una hipérbola con ecuación general 4x² - 9y² -16x -18y -29 = 0

Solución:

En este primer paso, vamos agrupar en el lado izquierdo los términos que contengan a las mismas variables y de lado derecho las que sean constantes.

$\displaystyle \left( 4{{x}^{2}}-16x \right)-\left( 9{{y}^{2}}+18y \right)=29$

Ahora vamos a factorizar en cada grupo el coeficiente del término al cuadrado:

$\displaystyle 4\left( {{x}^{2}}-4x \right)-9\left( {{y}^{2}}+2y \right)=29$

Se completa el trinomio al cuadrado perfecta en cada grupo, recordar que se agrega el mismo valor en el miembro derecho.

$\displaystyle 4\left( {{x}^{2}}-4x+{{\left( \frac{4}{2} \right)}^{2}} \right)-9\left( {{y}^{2}}+2y+{{\left( \frac{2}{2} \right)}^{2}} \right)=29+16-9$

De aquí obtenemos:

$\displaystyle 4\left( {{x}^{2}}-4x+4 \right)-9\left( {{y}^{2}}+2y+1 \right)=36$

Se agregó 16 en el lado derecho porque el resultado se multiplica por el 4 fuera del paréntesis, lo mismo ocurre con el otro grupo, se agregó un 9 al lado derecho porque al multiplicar el 9 por 1 obtenemos como resultado 9.

Factorizando los trinomios al cuadrado perfecto de cada grupo en el miembro izquierdo, obtenemos lo siguiente:

$\displaystyle 4{{\left( x-2 \right)}^{2}}-9{{\left( y+1 \right)}^{2}}=36$

Dividiendo ambos lados de la igualdad por 36 y simplificando:

$\displaystyle \frac{4{{\left( x-2 \right)}^{2}}}{36}-\frac{9{{\left( y+1 \right)}^{2}}}{36}=\frac{36}{36}$

Obtenemos lo siguiente:

$\displaystyle \frac{{{\left( x-2 \right)}^{2}}}{9}-\frac{{{\left( y+1 \right)}^{2}}}{4}=1$

Dónde:

$\displaystyle {{a}^{2}}=9$

$\displaystyle {{b}^{2}}=4$

Es decir:

$\displaystyle a=3$

$\displaystyle b=2$

Par obter "c" , podemos hacer uso de la siguiente condición:

$\displaystyle c=\sqrt{{{a}^{2}}+{{b}^{2}}}$

Sustituyendo los valores en la fórmula:

$\displaystyle c=\sqrt{9+4}=\sqrt{13}\approx 3.6$

c ≈ 3.6

Si observamos la fracción positiva la posee "x", por lo que se trata de una hipérbola horizontal.

A partir de este punto, podemos obtener los elementos de la hipérbola fuera del origen.

1️⃣ Obteniendo el Centro:

De la ecuación (x - h) tenemos (x -2), por lo que:

h = 2

De la ecuación (y - k) tenemos (y +1), por lo que:

k = -1

Finalmente el centro posee coordenadas:

C(2, -1)

2️⃣ Obteniendo el Vértice

$\displaystyle V(h\pm a,k)$

Entonces, las dos coordenadas para los vértices son:

$\displaystyle {{V}_{1}}(2-3,-1)={{V}_{1}}(-1,-1)$

$\displaystyle {{V}_{2}}(2+3,-1)={{V}_{2}}(5,-1)$

3️⃣ Obteniendo los Focos

$\displaystyle F(h\pm c,k)$

Entonces, las dos coordenadas para los focos son:

$\displaystyle {{F}_{1}}(2-3.6,-1)={{F}_{1}}\left( -1.6,-1 \right)$

$\displaystyle {{F}_{2}}(2+3.6,-1)={{F}_{2}}\left( 5.6,-1 \right)$

4️⃣ Obteniendo las ecuaciones de las asíntotas

Primera asíntota

$\displaystyle {{l}_{1}}:y-k=\frac{b}{a}\left( x-h \right)$

Sustituyendo los datos que tenemos en la fórmula:

$\displaystyle y-(-1)=\frac{2}{3}\left( x-2 \right)$

Resolviendo las operaciones e igualando a cero

$\displaystyle {{l}_{1}}:2x-3y-7=0$

Segunda asíntota

$\displaystyle {{l}_{2}}:y-k=-\frac{b}{a}\left( x-h \right)$

Sustituyendo los datos que tenemos en la fórmula:

$\displaystyle y-(-1)=-\frac{2}{3}\left( x-2 \right)$

Resolviendo las operaciones e igualando a cero

$\displaystyle {{l}_{2}}:2x+3y-1=0$

5️⃣ Gráfica de la Hipérbola

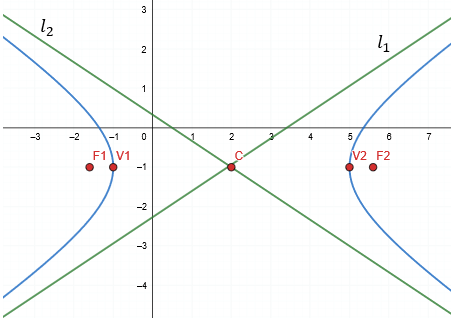
Hipérbola horizontal

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

4 Comentarios Publicados

Luis Valverde Avilés dice:

18 julio, 2019 a las 3:02 pm

Sólo para corregir, que en la ecuación se añadió un -9 en el término de la derecha, porque en la izquierda para completar el trinomio cuadrado se aumentó -1 que al multiplicar por 9 se convierte en -9. En la operación de la derecha quedaría 29+16-9, lo cual da efectivamente 36.

Responder
1. Carlos julián dice:
  
  9 abril, 2021 a las 5:45 pm
  
  Así es, ya se corrigió!
  
  Responder
Andres L Torres dice:

17 marzo, 2020 a las 4:57 pm

eso esta mal no. el resultado de la suma no es 36 el resultado de multiplicar 4 (4) =16 + 9 (1) =9 entonces 16+9=25 + 29 q nos da la ecuación hace un total de 54

Responder
1. Carlos julián dice:
  
  9 abril, 2021 a las 5:45 pm
  
  No es un error, es problema de la ecuación al final que se toma como suma, pero es resta. Al final es 16
  
  Responder

Deja una respuesta Cancelar la respuesta