Ecuación de la Recta en su forma Normal
Aunque muchas veces este método de Ecuación de la Recta en su forma Normal no se enseña o se explica en el nivel medio superior. Es importante tenerlo en cuenta porque nos puede servir más adelante en temas de matemáticas. Para comprender mucho mejor este artículo, tendremos que recurrir a la siguiente gráfica.
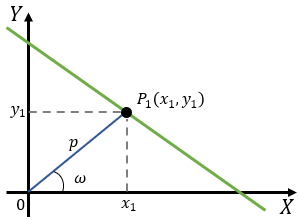
Si se observa la recta que por ecuación general tiene:
$\displaystyle Ax+By+C=0$
y que de longitud tiene un tamaño "p" y un ángulo que forma con la horizontal de "ω" grados. Podemos afirmar entonces que por el teorema de pitágoras.
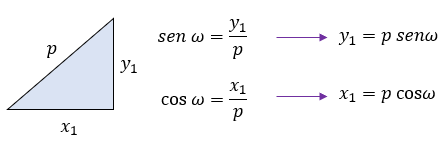
Si quisiéramos saber la pendiente de la recta OP (Origen al Punto P) , recordemos que la pendiente es la razón entre el incremento de "y" sobre el incremento de "x". Es decir:
$\displaystyle m=\tan \omega =\frac{{{y}_{1}}}{{{x}_{1}}}=\frac{psen\omega }{p\cos \omega }=\frac{sen\omega }{\cos \omega }$
Si observamos nuevamente la imagen de la gráfica, vamos a observar que el punto P(x1,y1), posee realmente las siguientes coordenadas:
$\displaystyle {{p}_{1}}(p\cos \omega ,psen\omega )$
La pendiente de la recta Ax + By + C = 0, al estar inclinada de lado izquierdo posee una pendiente negativa y estará dada de la siguiente forma:
$\displaystyle m=-\frac{\cos \omega }{sen\omega }$
Obteniendo la ecuación de la recta en su forma normal
Esto es importante, porque a partir de ahora podemos encontrar la ecuación de la recta punto pendiente (origen hasta el punto P) en su forma normal. Para ello, lo primero que haremos será colocar la ecuación punto - pendiente.
$\displaystyle y-{{y}_{1}}=m(x-{{x}_{1}})$
Datos:
$\displaystyle {{x}_{1}}=p\cos \omega $
$\displaystyle {{y}_{1}}=psen\omega $
$\displaystyle m=-\frac{\cos \omega }{sen\omega }$
Sustituyendo los datos en la fórmula punto - pendiente:
$\displaystyle y-psen\omega =-\frac{\cos \omega }{sen\omega }\left( x-p\cos \omega \right)$
$\displaystyle sen\omega \left( y-psen\omega \right)=-\cos \omega \left( x-p\cos \omega \right)$
Multiplicando:
$\displaystyle ysen\omega -pse{{n}^{2}}\omega =-x\cos \omega +p{{\cos }^{2}}\omega $
Igualando a cero:
$\displaystyle ysen\omega -pse{{n}^{2}}\omega +x\cos \omega -p{{\cos }^{2}}\omega =0$
Agrupando términos semejantes:
$\displaystyle x\cos \omega +ysen\omega -(psen{{\omega }^{2}}+p\cos {{\omega }^{2}})=0$
Factorizando a "p" por término común:
$\displaystyle x\cos \omega +ysen\omega -p(sen{{\omega }^{2}}+\cos {{\omega }^{2}})=0$
Por identidad trigonométrica:
$\displaystyle se{{n}^{2}}\omega +{{\cos }^{2}}\omega =1$
Aplicamos y obtenemos la ecuación de la recta en su forma normal

Se concluye que cualquier recta en su forma general:
$\displaystyle Ax+By+C=0$
Se puede expresar en su forma normal como:
$\displaystyle x\cos \omega +ysen\omega -p=0$
La forma normal de Ax + By + C = 0
La forma normal de la ecuación general Ax + By + C = 0 es la siguiente:
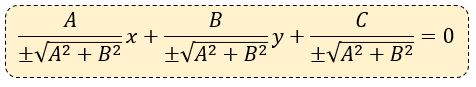
Los signos de r (radical) se consideran de la siguiente manera:
- Si C ≠ 0 , entonces el radical tendrá signo opuesto al de C.
- Si C = 0, el signo del radical se considerará igual al de B.
- Si C = B = 0, el signo del radical tendrá igual signo que A.
? Ejercicios Resueltos de la Ecuación Normal de la Recta
Solución:
Si tenemos la ecuación de la recta, ahora solo falta aplicar la fórmula y obtener los elementos para la nueva ecuación normal.
Datos:
A = √3
B = 1
C = -9
Ahora podemos encontrar el valor del radical:
$\displaystyle \sqrt{{{(\sqrt{3})}^{2}}+{{(1)}^{2}}}=\sqrt{3+1}=\sqrt{4}=2$
Esto es entonces:
$\displaystyle \frac{\sqrt{3}}{2}x+\frac{\sqrt{1}}{2}y-\frac{9}{2}=0$
Es decir:
$\displaystyle \frac{\sqrt{3}}{2}x+\frac{1}{2}y-\frac{9}{2}=0$
Ahora, podemos realizar la comparación con la ecuación en su forma normal:
$\displaystyle \cos \omega =\frac{\sqrt{3}}{2}$
$\displaystyle sen\omega =\frac{1}{2}$
$\displaystyle p=\frac{9}{2}$
Si despejamos a ω del seno o coseno, obtendremos el valor del ángulo.
$\displaystyle \omega =arcsen(\frac{1}{2})=30{}^\circ $
Como el seno y coseno son positivos, decimos que están en el primer cuadrante 😀
- Gráficamente esto es:
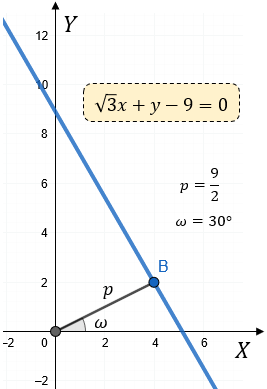
Solución:
Si tenemos la ecuación de la recta, ahora solo falta aplicar la fórmula y obtener los elementos para la nueva ecuación normal.
Datos:
A = 3
B = -4
C = -6
Ahora podemos encontrar el valor del radical:
$\displaystyle \sqrt{{{(3)}^{2}}+{{(-4)}^{2}}}=\sqrt{9+16}=\sqrt{25}=5$
$\displaystyle \frac{3}{5}x-\frac{4}{5}y-\frac{6}{5}=0$
Ahora, podemos realizar la comparación con la ecuación en su forma normal:
$\displaystyle \cos \omega =\frac{3}{5}$
$\displaystyle sen\omega =-\frac{4}{5}$
$\displaystyle p=\frac{6}{5}$
Si despejamos a ω del seno o coseno, obtendremos el valor del ángulo.
$\displaystyle \omega =arcsen\left( -\frac{4}{5} \right)=-53.13{}^\circ $
Como el coseno es positivo, y el seno es negativo. Decimos qué el ángulo de "ω" está en el 4to cuadrante.
$\displaystyle \omega =360{}^\circ -53.13{}^\circ =306.87{}^\circ $
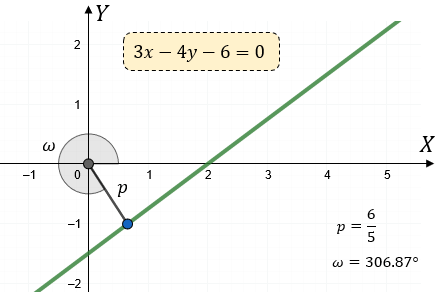
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Cómo sabes en que cuadrante se encuentra W?
-
Hola que tal! muchas gracias por el aporte, es muy claro y concreto. Me fue de mucha utilidad.
En la parte donde se menciona que la pendiente es la razón entre el incremento de “y” sobre el incremento de “x”. Es decir: senW / cosW, pero al estar inclinada de lado izquierdo, esta es negativa, entonces: m = - (senW / cosW), pero en el escrito estas se encuentran invertidas, es decir:
- (cosW / senW), ¿porqué sucede esto?
3 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar