Ecuación de la Parábola con Vértice fuera del Origen

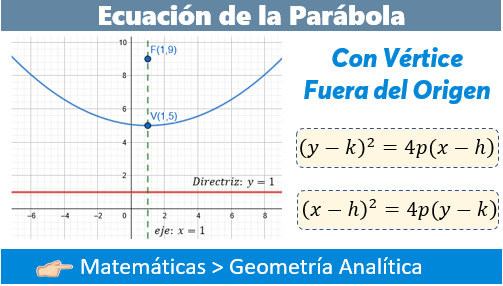
Después de analizar el caso de la parábola con vértice en el origen, ahora toca el estudio de la ecuación de la parábola con vértice fuera del origen, que es prácticamente muy sencillo si le entendemos desde el comienzo. Así que veamos como resolver este tipo de problemas, pero primero comprendamos como está estructurado los elementos de la parábola.

Veamos la siguiente gráfica:

Elementos y Ecuación de la Parábola con Vértice fuera del Origen

Las parábolas se caracterizan por tener un vértice, un foco, una directriz, una ecuación del eje, el lado recto, la concavidad (hacía donde abre), y finalmente la ecuación ordinaria, todo varía dependiendo del tipo de parábola que tengamos, puede ser una parábola horizontal o una parábola vertical.

🔹 Parábola Horizontal con Vértice (h, k)

Veamos la gráfica

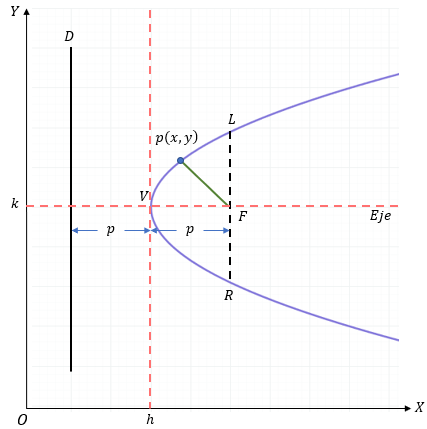
Vemos que se trata de una parábola horizontal, y que su vértice está fuera del origen. Su eje es paralelo al eje "X" y es cóncava hacia la derecha o izquierda, según sea el caso.

Ecuación Ordinaria

La ecuación ordinaria para este tipo de parábola horizontal es la siguiente:

Ecuación General

La ecuación general de la parábola es la siguiente:

$\displaystyle C{{y}^{2}}+Dx+Ey+F=0$

Elementos de la parábola

Se considera que la parábola posee su vértice "V" justamente en el punto (h,k) "Note las líneas punteadas color naranja en la gráfica".

1️⃣ Vértice:

$\displaystyle V(h,k)$

2️⃣ Foco:

$\displaystyle F(h+p,k)$

3️⃣ Directriz:

$\displaystyle \overline{D{D}'}:x=h-p$

4️⃣ Lado Recto:

5️⃣ Ecuación del eje:

$\displaystyle y=k$

Concavidad

🔸 Si p > 0 entonces se dice que la parábola será cóncava hacia la derecha.

🔸 Si p < 0 entonces se dice que la parábola será cóncava hacia la izquierda.

🔹 Parábola Vertical con Vértice (h, k)

Veamos la gráfica:

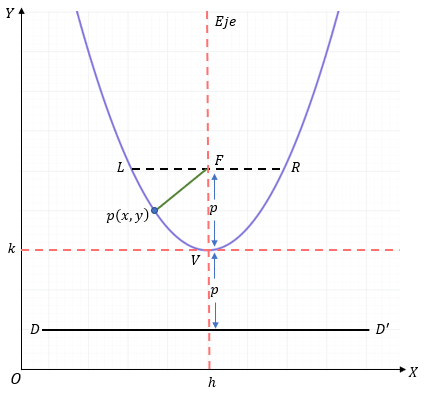
Ecuación Ordinaria

La ecuación ordinaria para este tipo de parábola horizontal es la siguiente:

Ecuación General

La ecuación general de la parábola es la siguiente:

$\displaystyle A{{x}^{2}}+Dx+Ey+F=0$

Elementos de la parábola

Se considera que la parábola posee su vértice "V" justamente en el punto (h,k) "Note las líneas punteadas color naranja en la gráfica".

1️⃣ Vértice:

$\displaystyle V(h,k)$

2️⃣ Foco:

$\displaystyle F(h,k+p)$

3️⃣ Directriz:

$\displaystyle \overline{D{D}'}:y=k-p$

4️⃣ Lado Recto:

5️⃣ Ecuación del eje:

$\displaystyle x=h$

Concavidad

🔸 Si p > 0 entonces se dice que la parábola será cóncava hacia arriba.

🔸 Si p < 0 entonces se dice que la parábola será cóncava hacia abajo.

Ejercicios Resueltos de la Parábola con Vértice fuera del Origen

Veamos algunos ejemplos resueltos para la parábola con vértice fuera del origen.

Solución:

Si graficamos los dos puntos que nos dan como referencia, que es el vértice y foco podremos saber hacía donde abrirá nuestra parábola, e incluso el tipo de ecuación que usará. Veamos:

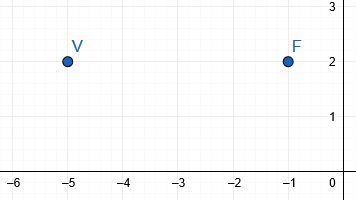
Al ver la imagen sabemos que se trata de una parábola que abre hacia la derecha, y que tiene su eje paralelo al eje "x".  Por lo que la ecuación de dicha parábola tendrá la siguiente forma:

$\displaystyle {{(y-k)}^{2}}=4p(x-h)$

Si el vértice tiene coordenadas (-5 ,2)

Entonces:

h = -5

k = 2

El foco tiene coordenadas ( -1 , 2), la distancia que hay desde el vértice al foco es de 4 unidades, lo podemos medir gráficamente o lo podemos calcular mediante su fórmula, veamos:

$\displaystyle F(h+p,k)$

Si sabemos que:

$\displaystyle h+p=-1$

Pero también sabemos que h = -5

$\displaystyle -5+p=-1$

Despejando a "p"

$\displaystyle p=-1+5=4$

Por lo que

p = 4

Ahora, sustituimos nuestros datos en la fórmula:

$\displaystyle {{(y-k)}^{2}}=4p(x-h)$

$\displaystyle {{(y-2)}^{2}}=4(4)(x-(-5))$

Resolviendo las operaciones básicas

$\displaystyle {{y}^{2}}-4y+4=16x+80$

Igualamos la ecuación a cero

$\displaystyle {{y}^{2}}-4y+4-16x-80=0$

Ordenando y reduciendo:

 Resultado:

$\displaystyle {{y}^{2}}-4y-16x-76=0$

Veamos la gráfica de nuestra parábola:

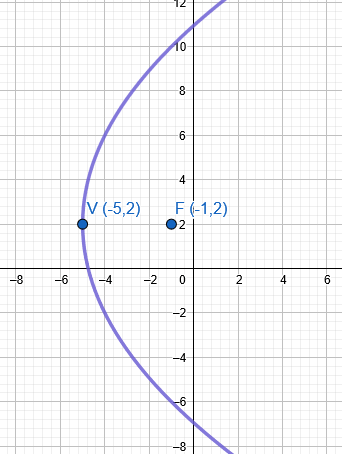
Solución:

Al observar la ecuación de la parábola, podemos darnos cuenta que el término cuadrático lo posee "x", entonces se trata de una parábola horizontal, para comenzar a resolver este tipo de problemas, agrupamos los términos con "y" en el primer miembro de la igualdad.

$\displaystyle {{x}^{2}}-2x=16y-81$

Paso 1: Se completa el trinomio al cuadrado perfecto en el primer miembro, y después se factoriza.

$\displaystyle {{x}^{2}}-2x+1=16y-81+1$

$\displaystyle {{(x-1)}^{2}}=16y-80$

Paso 2: Se factoriza el segundo miembro de la igualdad, tomando como factor común a 16

$\displaystyle {{(x-1)}^{2}}=16(y-5)$

La ecuación que se obtiene es de la forma: (y-k)²=4p (x-h)

Donde:

h = 1

k = 5

p = 4

¿Por qué p = 4?

$\displaystyle \begin{array}{*{35}{l}}
4p=16 \\
p=\frac{16}{4}=4 \\
\end{array}$

Encontrando los elementos de la parábola.

a) Obteniendo el Vértice de la Parábola

Para el vértice, debemos aplicar la fórmula V(h,k)

$\displaystyle V(h,k)=(1,5)$

b) Obteniendo el foco

$\displaystyle F(h,k+p)=(1,5+4)=(1,9)$

$\displaystyle F(1,9)$

c) Obteniendo la directriz

$\displaystyle y=k-p=5-4=1$

$\displaystyle y=1$

d) Obteniendo el Lado Recto

$\displaystyle LR=\left| 4p \right|=\left| 4(4) \right|=\left| 16 \right|=16$

$\displaystyle LR=16$

e) Obteniendo la ecuación del eje

$\displaystyle x=h=1$

$\displaystyle x=1$

f) Obtener la gráfica de la parábola

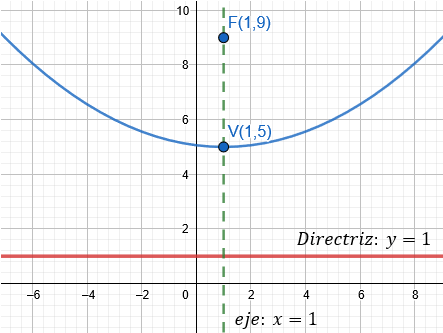
🏆 Ejercicios para Practicar con Solución

Ahora es momento de practicar 😀

💥 Ver Solución