Ecuación de la Parábola con Vértice en el Origen

Dentro de nuestro estudio de la geometría analítica, nos encontramos con el tema de la Parábola, y este a su vez se derivan en dos grandes secciones. Los problemas de la parábola con vértice en el origen y la parábola con vértice fuera del origen.

Antes de profundizar el tema con ejemplos y ejercicios resueltos. Veamos primero la definición de la Parábola.

Elementos y Ecuación de una Parábola

Para comprender mucho mejor el tema, veamos la siguiente imagen de las partes de la parábola o elementos de una parábola. Pero comenzaremos con una parábola horizontal.

🔸 Parábola Horizontal

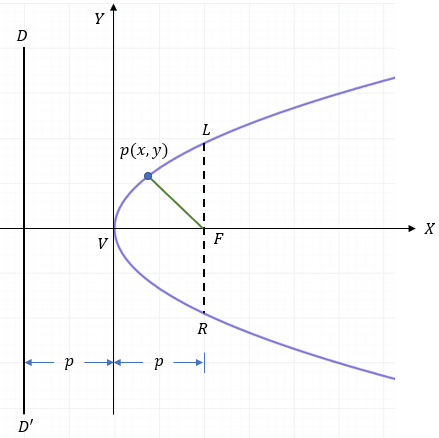
En una parábola horizontal el foco "F" está sobre el eje X, y son cóncavas hacia la derecha o a la izquierda.

En nuestra imagen vemos a la letra "p", que significa parámetro es decir (la distancia del vértice al foco o a la directriz).

Ecuación Canónica

Su ecuación canónica para una parábola horizontal es la siguiente:

Elementos de la Parábola

Se considera que la parábola posee su vértice "V" justamente en el centro (0,0). Entonces sus elementos estarán distribuidas de la siguiente forma:

1️⃣ Foco:

$latex \displaystyle F(p,0)$

2️⃣ Directriz: 

$latex \displaystyle \overline{DD'}:x=-p$

3️⃣ Ecuación del eje:

$latex \displaystyle y=0$

4️⃣ Lado Recto:

$latex \displaystyle \overline{LR}=\left| 4p \right|$

Concavidad

🔹 Si p > 0 entonces decimos que la parábola abre hacia la derecha.

🔹 Si p < 0 entonces decimos que la parábola abre hacia la izquierda.

🔸 Parábola Vertical

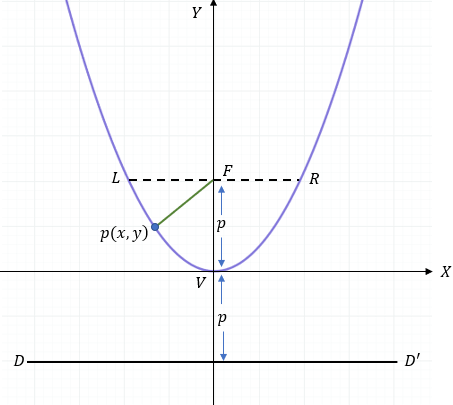
En una parábola vertical el foco "F" está sobre el eje Y, y son cóncavas hacia arriba o hacia abajo.

Ecuación Canónica

Su ecuación canónica para una parábola vertical es la siguiente:

Elementos de la Parábola

Se considera que la parábola posee su vértice "V" justamente en el centro (0,0). Entonces sus elementos estarán distribuidas de la siguiente forma:

1️⃣ Foco:

$latex \displaystyle F(0,p)$

2️⃣ Directriz: 

$latex \displaystyle \overline{DD'}:y=-p$

3️⃣ Ecuación del eje:

$latex \displaystyle x=0$

4️⃣ Lado Recto:

$latex \displaystyle \overline{LR}=\left| 4p \right|$

Concavidad

🔹 Si p > 0 entonces decimos que la parábola es cóncava hacia arriba.

🔹 Si p < 0 entonces decimos que la parábola es cóncava hacia abajo.

Ejercicios Resueltos de la Ecuación de la Parábola con Vértice en el Origen

Solución:

Vamos a escribir la ecuación en la forma canónica, es decir:

$latex \displaystyle {{y}^{2}}=4px$

Entonces simplemente despejamos a y², y tendremos lo siguiente:

$latex \displaystyle {{y}^{2}}=4x$

Esto quiere decir que al igualar ambas ecuaciones tendremos:

$latex \displaystyle 4px=4x$

Simplificando, esto nos queda:

$latex \displaystyle p=1$

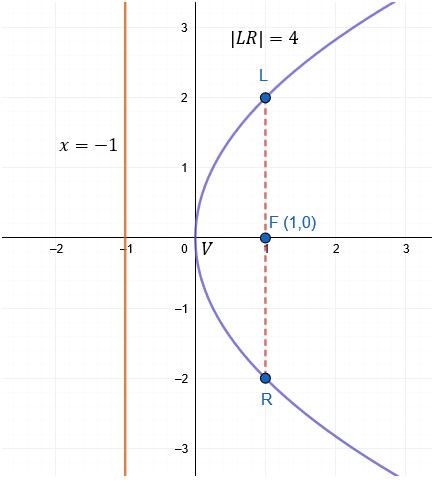
Por la forma de la ecuación sabemos que se trata de una parábola horizontal, que abre hacia la derecha, porque p > 0, sustituyendo este dato en las fórmulas, sabremos los valores de los elementos.

Foco : F (p, 0) = F (1, 0)

Directriz: x = - p → x = -1

Lado Recto: LR = | 4 (1) | = 4

Eje: y = 0

De forma gráfica tenemos:

Solución:

Si la parábola coincide con el eje "x" entonces estamos hablando de una parábola horizontal. Como la curva pasa por el punto A (3, 6), sus coordenadas deben satisfacer dicha ecuación de la parábola, de tal forma que:

$latex \displaystyle {{y}^{2}}=4px$

Sustituyendo x = 3 , y = 6 en la ecuación, tenemos:

$latex \displaystyle {{\left( 6 \right)}^{2}}=4p\left( 3 \right)$

Esto nos da:

$latex \displaystyle 36=12p$

Despejando a "p"

$latex \displaystyle p=\frac{36}{12}=3$

Por lo que:

$latex \displaystyle p=3$

Con este dato, podemos avanzar sin problemas. Si p = 3, la ecuación de la parábola es:

$latex \displaystyle {{y}^{2}}=4(3)x=12x$

Es decir:

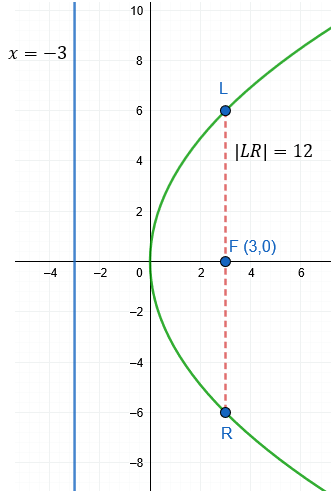
a) Ecuación de la parábola

$latex \displaystyle {{y}^{2}}=12x$

b) Coordenadas del foco

$latex \displaystyle F(3,0)$

c) Ecuación de la directriz

$latex \displaystyle x=-3$

d) Longitud del lado recto

$latex \displaystyle LR=|4(3)|=12$

e) Gráfica de la parábola

Solución:

Al observar la ecuación que tiene la forma canónica de x² = 4py, nos indica que es una parábola vertical. Y que además para encontrar al parámetro "p", solo bastará con igualar ambas ecuaciones como se muestra:

$latex \displaystyle 4py=16y$

Simplificando

$latex \displaystyle 4p=16$

Despejando "p"

$latex \displaystyle p=\frac{16}{4}=4$

Es decir:

$latex \displaystyle p=4$

Con este dato del parámetro, podemos encontrar los elementos de la parábola:

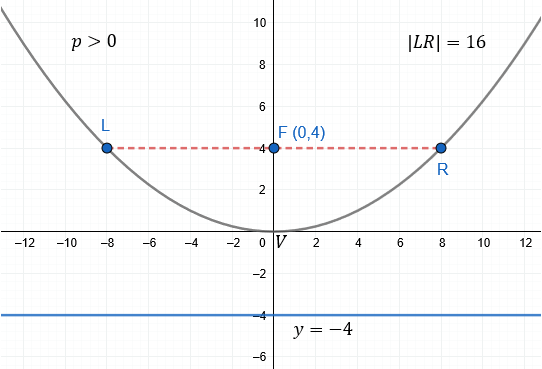
a) Ecuación de la parábola

$latex \displaystyle {{x}^{2}}=16y$

b) Coordenadas del foco

$latex \displaystyle F(0,4)$

c) Ecuación de la directriz

$latex \displaystyle y=-4$

d) Longitud del lado recto

$latex \displaystyle LR=|4(4)|=16$

e) Gráfica de la parábola