Ecuación de la Recta Punto - Pendiente - Ejercicios Resueltos

Dentro de la geometría analítica, la ecuación punto - pendiente es muy importante en una de las ecuaciones de la recta, y que la podemos encontrar en nuestro libro de matemáticas, de la siguiente forma:

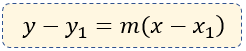
La ecuación es útil cuando sabemos dos cosas:

• Un punto en la línea.
• La pendiente de la recta.

Ya que sabemos la fórmula, la pregunta que nos hacemos es la siguiente. ¿Qué significa la ecuación de punto - pendiente?

La Ecuación Punto - Pendiente de una recta

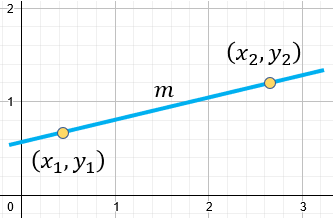
Podemos observar que:

$\displaystyle \left( {{x}_{1}},{{y}_{1}} \right)$ = Es un punto conocido

$\displaystyle \left( {{x}_{2}},{{y}_{2}} \right)$ = Es otro punto conocido

$\displaystyle m$ = Es la pendiente de la recta

La pendiente le podemos dar un sentido gráfico, de esta forma. (Observar la imagen).

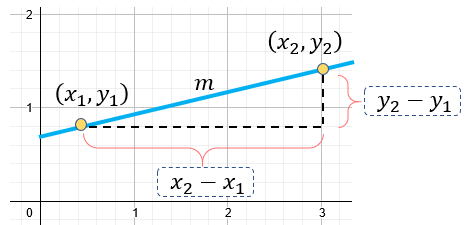
Recordemos la fórmula de la pendiente:

$\displaystyle m=\frac{y-{{y}_{1}}}{x-{{x}_{1}}}$

De acá mismo, podemos hacer el despeje de y - y1, para que nos quede la ecuación que ya conocemos, ejemplo:

$\displaystyle y-{{y}_{1}}=m(x-{{x}_{1}})$

Ejercicios Resueltos de la Ecuación de la Recta Punto - Pendiente

Para entender mucho mejor el tema, veamos los siguientes ejemplos resueltos, paso a paso 😀

Solución:

El único punto que tenemos es (4, -5), que lo podemos asociar a $\displaystyle ({{x}_{1}},{{y}_{1}})$ y lógicamente m = 3, dicho de otra forma:

$\displaystyle {{x}_{1}}=4$

$\displaystyle {{y}_{1}}=-5$

$\displaystyle m=3$

Si la ecuación de la recta es:

$\displaystyle y-{{y}_{1}}=m(x-{{x}_{1}})$

Vamos a sustituir nuestros datos, en dicha fórmula:

$\displaystyle y-\left( -5 \right)=3(x-4)$

Simplificando

$\displaystyle y+5=3x-12$

Igualando todo a cero.

$\displaystyle 3x-12-y-5=0$

Nuevamente, simplificamos:

$\displaystyle 3x-y-17=0$

 Resultado:

Ecuación de la Recta: $\displaystyle 3x-y-17=0$

De forma gráfica, esto es:

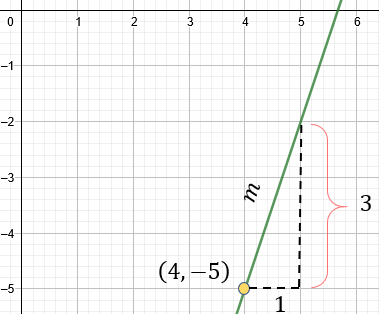
Solución:

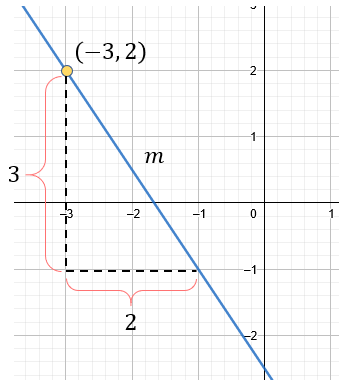
Basándonos en nuestros datos del segundo ejercicio, podemos apreciar que nuestro punto posee coordenadas (-3,2), y que la pendiente es negativa, equivalente a -3/2. Dicho de otra forma, tenemos estos datos.

$\displaystyle {{x}_{1}}=-3$

$\displaystyle {{y}_{1}}=2$

$\displaystyle m=-\frac{3}{2}$

Si la ecuación de la recta es:

Vamos a sustituir nuestros datos, en la fórmula:

$\displaystyle y-2=-\frac{3}{2}(x-(-3))$

Simplificando.

$\displaystyle y-2=-\frac{3}{2}(x+3)$

Multiplicando lo del segundo miembro, en el primero.

$\displaystyle 2(y-2)=-3(x+3)$

Realizando el producto

$\displaystyle 2y-4=-3x-9$

Igualando a cero

$\displaystyle 2y-4+3x+9=0$

Ordenando e igualando.

 Resultado:

$\displaystyle 3x+2y+5=0$

De forma gráfica, tenemos:

Ahora, vamos a intentar resolver un ejemplo, teniendo en cuenta la gráfica, es decir. Vamos a proporcionar gráficamente tanto al punto, como a la pendiente para poder encontrar la ecuación de la recta. 

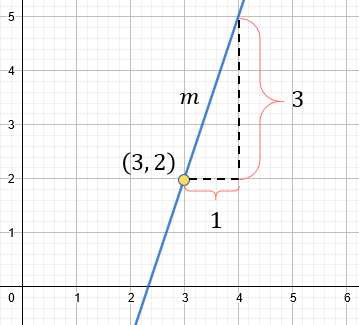
Solución: 

Para poder resolver este tipo de problemas iniciando con el gráfico, es importante verificar los datos que tenemos, y colocarlos tal como lo interpretamos. Por ejemplo, tenemos un punto con coordenadas (3,2) y una pendiente de 3. Es decir:

$\displaystyle {{x}_{1}}=3$

$\displaystyle {{y}_{1}}=2$

$\displaystyle m=\frac{3}{1}=3$

Al tener nuestros datos, podemos simplemente sustituir en nuestra fórmula de ecuación punto - pendiente y resolver, sin problemas.

$\displaystyle y-2=3(x-3)$

Multiplicando

$\displaystyle y-2=3x-9$

Igualando a cero

$\displaystyle 3x-9-y+2=0$

Y finalmente, tenemos:

 Resultado:

$\displaystyle 3x-y-7=0$

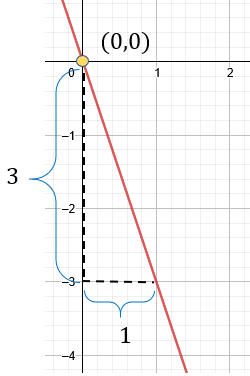
Solución:

Para este ejemplo, vemos que nuestra recta pasa exactamente en el punto (0,0), es decir, pasa por el origen. Esto es muy importante porque nuestra ecuación será muy fácil de resolver. Nuestra pendiente si observamos vemos que es negativa , esto es porque la recta se inclina de lado izquierdo y no derecho. Entonces, tenemos:

$\displaystyle {{x}_{1}}=0$

$\displaystyle {{y}_{1}}=0$

$\displaystyle m=-\frac{3}{1}=-3$

Si sustituimos estos valores, en nuestra ecuación, vamos a obtener que:

$\displaystyle y-0=-3\left( x-0 \right)$

Simplificamos y multiplicamos

$\displaystyle y=-3x-0$

Simplificando aún más

$\displaystyle y=-3x$

Igualando a cero, finalmente tenemos:

 Resultado:

$\displaystyle 3x+y=0$

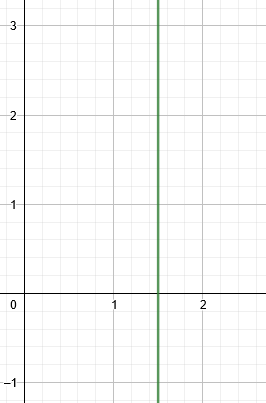
Solución:

Lo que observamos es una recta totalmente vertical, ¿cuál será su pendiente?. Para este tipo de rectas, la pendiente no está definida. De hecho podemos decir que se trata de un caso especial , y se utiliza una ecuación diferente para describirla.

$\displaystyle x=1.5$

Cada punto en la línea tiene coordenadas x = 1.5 , por eso su ecuación es de la misma forma.