Leyes de Kepler - 15 Ejercicios Resueltos + [PDF]
¡Buen día lectores! Para entender cómo se mueve el universo, debemos retroceder antes de Newton y mirar al cielo con los ojos de Johannes Kepler. Hoy no solo aprenderás historia; dominarás las 3 Leyes que rigen el movimiento de planetas, satélites y cometas con ejercicios prácticos.
¿Qué aprenderás hoy?
Dominarás:
- 1ª Ley: Por qué las órbitas son elipses y no círculos.
- 2ª Ley: Por qué los planetas aceleran cuando se acercan al Sol.
- 3ª Ley: Fórmulas matemáticas para calcular periodos y distancias.
- 5 Ejercicios Resueltos paso a paso.
- Guía PDF descargable.
¿Quién fue Johannes Kepler?
Johannes Kepler
1571-1630
Astrónomo y matemático alemán. Fue ayudante del gran observador Tycho Brahe. Usando los datos precisos de Brahe sobre Marte, Kepler rompió con dos milenios de tradición astronómica: descubrió que los planetas no se mueven en círculos perfectos, sino en elipses.

Primera Ley de Kepler: Ley de las Órbitas
1ª Ley de Kepler
Todos los planetas se mueven alrededor del Sol describiendo trayectorias elípticas, estando el Sol situado en uno de los focos de la elipse.
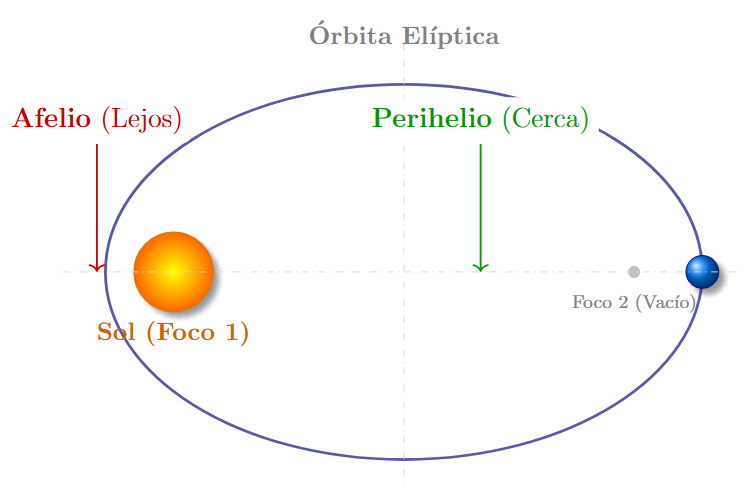
Esto define dos puntos clave en la órbita:
- Perihelio: El punto más cercano al Sol.
- Afelio: El punto más lejano al Sol.
Ejercicio Conceptual 1 (1ª Ley)
Si la Tierra estuviera en el centro de una órbita perfectamente circular, ¿existirían las estaciones del año?
Solución:
Las estaciones del año NO dependen de la distancia al Sol (que varía poco en la elipse terrestre), sino de la inclinación del eje terrestre. Sin embargo, en una órbita circular perfecta, la distancia sería constante todo el año, eliminando el perihelio y el afelio.
La Excentricidad (\(e\)): ¿Qué tan "achatada" es la elipse?
No todas las elipses son iguales. Algunas parecen casi círculos y otras parecen cigarros alargados. Kepler definió esto mediante la excentricidad (\(e\)).
- Si \( e = 0 \): La órbita es un Círculo perfecto.
- Si \( 0 < e < 1 \): La órbita es una Elipse.
- Si \( e = 1 \): La trayectoria es una Parábola (el objeto escapa y no regresa).
💡 Dato Curioso
La órbita de la Tierra tiene una excentricidad muy baja (\(e \approx 0.0167\)), por eso parece un círculo a simple vista. En cambio, el cometa Halley tiene \(e \approx 0.967\), lo que significa que su órbita es extremadamente alargada.
Segunda Ley de Kepler: Ley de las Áreas
Esta ley explica la velocidad de los planetas. ¿Van siempre a la misma velocidad? La respuesta es NO.
2ª Ley de Kepler
El radio vector que une al planeta y el Sol barre áreas iguales en tiempos iguales.
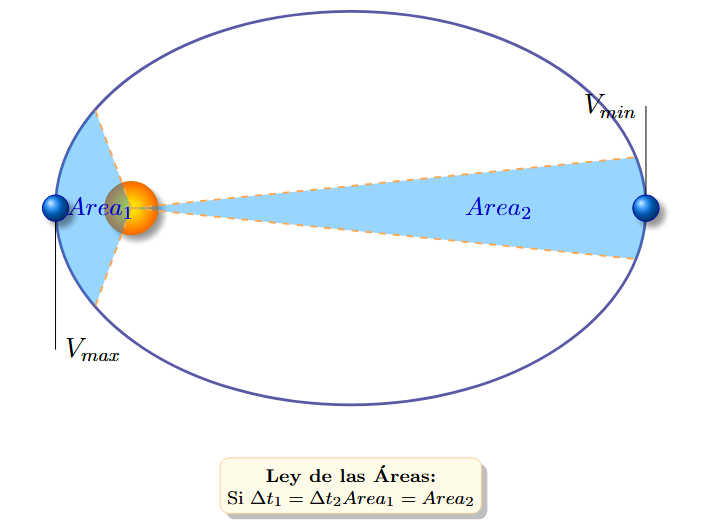
Consecuencia Práctica
Para barrer la misma área, el planeta debe moverse más rápido en el Perihelio (cerca del Sol) y más lento en el Afelio (lejos del Sol).
Ejercicio Conceptual 2 (2ª Ley)
Un cometa tiene una órbita muy elíptica. ¿En qué punto su energía cinética es máxima?
Solución:
En el Perihelio. Según la 2ª Ley, ahí su velocidad es máxima. Como $E_c = \frac{1}{2}mv^2$, a mayor velocidad, mayor energía cinética.
Velocidad Orbital: ¿Por qué cambia?
Gracias a la segunda ley, sabemos que la velocidad de un planeta no es constante. Esto se debe a la conservación del momento angular.
- En el Perihelio (Cerca del Sol): La gravedad es más fuerte, por lo que el planeta "cae" más rápido alrededor de la estrella. La velocidad es MÁXIMA.
- En el Afelio (Lejos del Sol): La gravedad es más débil y el planeta se mueve más lento. La velocidad es MÍNIMA.
Tercera Ley de Kepler: Ley de los Periodos (Fórmulas)
Aquí entra la matemática fuerte. Esta ley relaciona el tiempo que tarda un planeta en dar la vuelta (Periodo, $T$) con su distancia media al Sol ($r$).
\[ T^2 = K \cdot r^3 \]
Donde $K$ es una constante que depende de la masa del cuerpo central (el Sol).
Para comparar dos planetas que orbitan la misma estrella, usamos:
\[ \frac{T_1^2}{r_1^3} = \frac{T_2^2}{r_2^3} \]
✅ Ejercicios Resueltos de la Tercera Ley de Kepler
Vamos a resolver problemas numéricos, que es lo que suelen pedir en los exámenes.
Ejemplo 1: Masa de la Tierra (Nivel Avanzado)
La Luna orbita la Tierra a una distancia media de $3.84 \times 10^8$ m y tiene un periodo de 27.3 días. Calcule la masa de la Tierra.
Solución:
Primero convertimos el periodo a segundos:
$T = 27.3 \text{ días} \times 86400 \text{ s/día} = 2.36 \times 10^6 \text{ s}$.
Usamos la fórmula de Newton-Kepler despejada para la Masa ($M$):
\[ T^2 = \frac{4\pi^2}{GM} r^3 \Rightarrow M = \frac{4\pi^2 r^3}{G T^2} \]
Sustituimos ($G = 6.67 \times 10^{-11}$):
\[ M = \frac{4(3.1416)^2 (3.84 \times 10^8)^3}{(6.67 \times 10^{-11})(2.36 \times 10^6)^2} \]
\[ M = \frac{39.48 \times (5.66 \times 10^{25})}{3.71 \times 10^2} \]
\[ M \approx 6.02 \times 10^{24} \text{ kg} \]
Resultado: La masa de la Tierra es aprox. $6 \times 10^{24}$ kg.
Ejemplo 2: Comparación Tierra-Júpiter
La Tierra está a 1 UA (Unidad Astronómica) del Sol y tarda 1 año en orbitar. Júpiter está a 5.2 UA. ¿Cuánto dura un "año" en Júpiter?
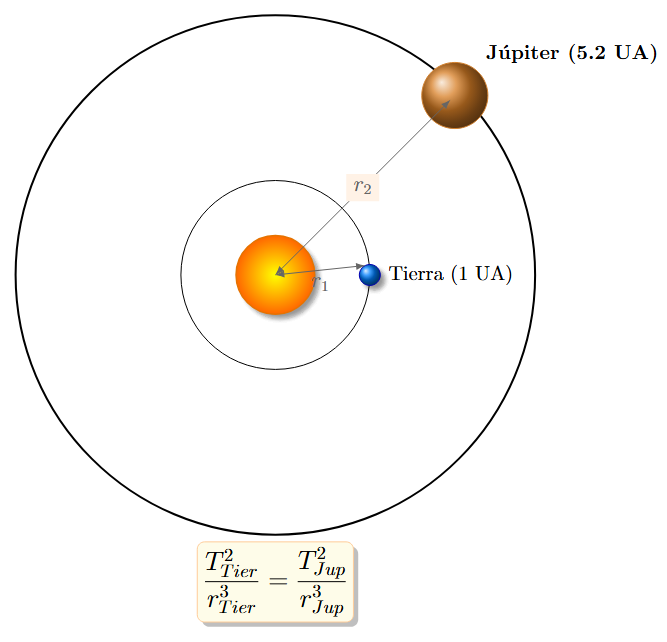
Solución:
Usamos la relación de comparación (Tierra=1, Júpiter=2):
\[ \frac{T_1^2}{r_1^3} = \frac{T_2^2}{r_2^3} \]
Como usamos años y UA, para la Tierra $\frac{1^2}{1^3} = 1$. Entonces:
\[ \frac{T_J^2}{(5.2)^3} = 1 \Rightarrow T_J^2 = (5.2)^3 \]
\[ T_J = \sqrt{(5.2)^3} = \sqrt{140.6} \approx 11.86 \text{ años} \]
Resultado: Júpiter tarda casi 12 años terrestres en dar una vuelta.
Ejemplo 3: Satélite Geoestacionario
Un satélite debe orbitar la Tierra cada 24 horas (periodo geoestacionario). Sabiendo que la Luna tarda 27.3 días y está a 384,000 km, ¿a qué altura debe estar el satélite?
Solución:
Datos:
Luna: $T_L = 27.3$ días, $r_L = 384,000$ km.
Satélite: $T_S = 1$ día (24h). Buscamos $r_S$.
\[ \frac{T_S^2}{r_S^3} = \frac{T_L^2}{r_L^3} \Rightarrow r_S^3 = T_S^2 \cdot \frac{r_L^3}{T_L^2} \]
\[ r_S^3 = (1)^2 \cdot \frac{(384000)^3}{(27.3)^2} = \frac{5.66 \times 10^{16}}{745.3} \]
\[ r_S^3 \approx 7.59 \times 10^{13} \]
\[ r_S = \sqrt[3]{7.59 \times 10^{13}} \approx 42,300 \text{ km} \]
Ojo: Esta es la distancia al centro de la Tierra. Restamos el radio terrestre (6,370 km) para la altura.
$h = 42,300 - 6,370 = 35,930$ km.
Resultado: Debe estar a unos 36,000 km de altura.
Ejemplo 4: Asteroide Misterioso
Solución:
Usando el sistema simplificado (Años-UA):
\[ T^2 = r^3 \Rightarrow r = \sqrt[3]{T^2} \]
\[ r = \sqrt[3]{8^2} = \sqrt[3]{64} = 4 \text{ UA} \]
Resultado: Está a 4 veces la distancia Tierra-Sol.
Ejemplo 6: El Cometa Halley
El famoso Cometa Halley tarda aproximadamente 76 años en dar una vuelta completa al Sol. Calcule la distancia media (semieje mayor) del cometa al Sol en Unidades Astronómicas (UA).
Solución:
Este problema es ideal para usar el sistema simplificado donde el tiempo se mide en años y la distancia en UA (tomando a la Tierra como referencia).
Fórmula simplificada:
\[ T^2 = r^3 \]
(Válido solo si \(T\) está en años y \(r\) en UA).
Datos: \(T = 76\) años.
Despeje:
\[ r = \sqrt[3]{T^2} \]
\[ r = \sqrt[3]{(76)^2} = \sqrt[3]{5776} \]
\[ r \approx 17.94 \text{ UA} \]
Resultado: Su distancia media es de 17.94 UA (se aleja más allá de Plutón y se acerca más que Venus).
Ejemplo 7: Altitud de un Satélite Espía
Un satélite espía orbita la Tierra con un periodo de 2 horas (7200 s). Sabiendo que la masa de la Tierra es \(5.97 \times 10^{24}\) kg y su radio es \(6371\) km, ¿a qué altura sobre la superficie se encuentra?
Solución:
Cuidado: La fórmula de Kepler nos da el radio de la órbita (\(r\)) desde el centro de la Tierra. Para hallar la altura (\(h\)), debemos restar el radio terrestre (\(R_T\)).
1. Calculamos el radio orbital (\(r\)):
Despejamos \(r\) de la 3ª Ley:
\[ r = \sqrt[3]{\frac{G M_T T^2}{4\pi^2}} \]
Sustituimos:
\[ r = \sqrt[3]{\frac{(6.67 \times 10^{-11})(5.97 \times 10^{24})(7200)^2}{4(3.1416)^2}} \]
\[ r = \sqrt[3]{\frac{2.06 \times 10^{22}}{39.48}} = \sqrt[3]{5.22 \times 10^{20}} \]
\[ r \approx 8.05 \times 10^6 \text{ m} = 8050 \text{ km} \]
2. Calculamos la altura (\(h\)):
\[ h = r - R_T \]
\[ h = 8050 \text{ km} - 6371 \text{ km} \]
\[ h = 1679 \text{ km} \]
Resultado: El satélite orbita a 1679 km de altura.
Descargar Guía: 15 Ejercicios de Leyes de Kepler [PDF]
¿Quieres profundizar? Descarga nuestra guía completa con problemas de examen.
🔒 Incluye Teoría y Problemas Resueltos • Gratis
Conclusión
Las leyes de Kepler transformaron la astronomía de una ciencia mística a una ciencia precisa. Recuerda que aunque Kepler describió CÓMO se mueven los planetas, fue Newton quien años después explicó POR QUÉ (la Gravedad).
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Necesito calcular la distancia que tiene el sol en todos los planetas con la tercera ley de Kepler.
por favor, ayuda. -
Muy buena su información
-
Que es GME?en las leyes de Kepler?
-
Muy buenos articulos. Ahora bien, es posible despejar tiempo a partit de la 2 ley?
-
Cuáles serían los ejercicios de la primera ley de kepler
16 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar