Límite Elástico y Curva Esfuerzo-Deformación

Hemos llegado al clímax de nuestra serie sobre elasticidad y propiedades mecánicas. En los artículos anteriores, exploramos las constantes elásticas ($E, G, K, \nu$) que describen el comportamiento lineal y reversible de los materiales. Pero, ¿qué sucede cuando aplicamos una fuerza tan grande que el material no vuelve a su forma original? 🤔

¿Cómo y cuándo se rompe? Para responder a estas preguntas, debemos analizar la curva esfuerzo-deformación completa y entender conceptos cruciales como el límite elástico y la deformación plástica.

Introducción

Hasta ahora, nos hemos movido en una zona de confort: la región elástica, donde los materiales se comportan como un resorte perfecto. Sin embargo, en el mundo real, los materiales pueden sufrir deformaciones permanentes o incluso fracturarse. La curva esfuerzo-deformación es el "mapa" más completo que existe para describir el viaje de un material desde que se le aplica una pequeña carga hasta que finalmente se rompe. Esta gráfica, obtenida generalmente de un ensayo de tracción, es como la huella dactilar de un material, revelando sus características de rigidez, resistencia, ductilidad y tenacidad.

Comprender la totalidad de esta curva es absolutamente crítico para la ingeniería. No solo nos permite diseñar componentes que operen de forma segura dentro de su límite elástico, sino que también nos ayuda a predecir cómo fallará una estructura en caso de una sobrecarga extrema. Este conocimiento es vital para diseñar con seguridad, seleccionar los materiales adecuados para cada aplicación y controlar procesos de manufactura como el doblado, el laminado o el forjado de metales, que dependen intrínsecamente de la deformación plástica.

La Curva Esfuerzo-Deformación: Un Mapa Completo

La curva esfuerzo-deformación se obtiene al someter una muestra estandarizada de un material (probeta) a una fuerza de tracción creciente y medir continuamente el esfuerzo y la deformación unitaria resultantes. Es importante notar que comúnmente se grafica el esfuerzo de ingeniería (fuerza dividida por el área inicial de la probeta) contra la deformación unitaria de ingeniería.

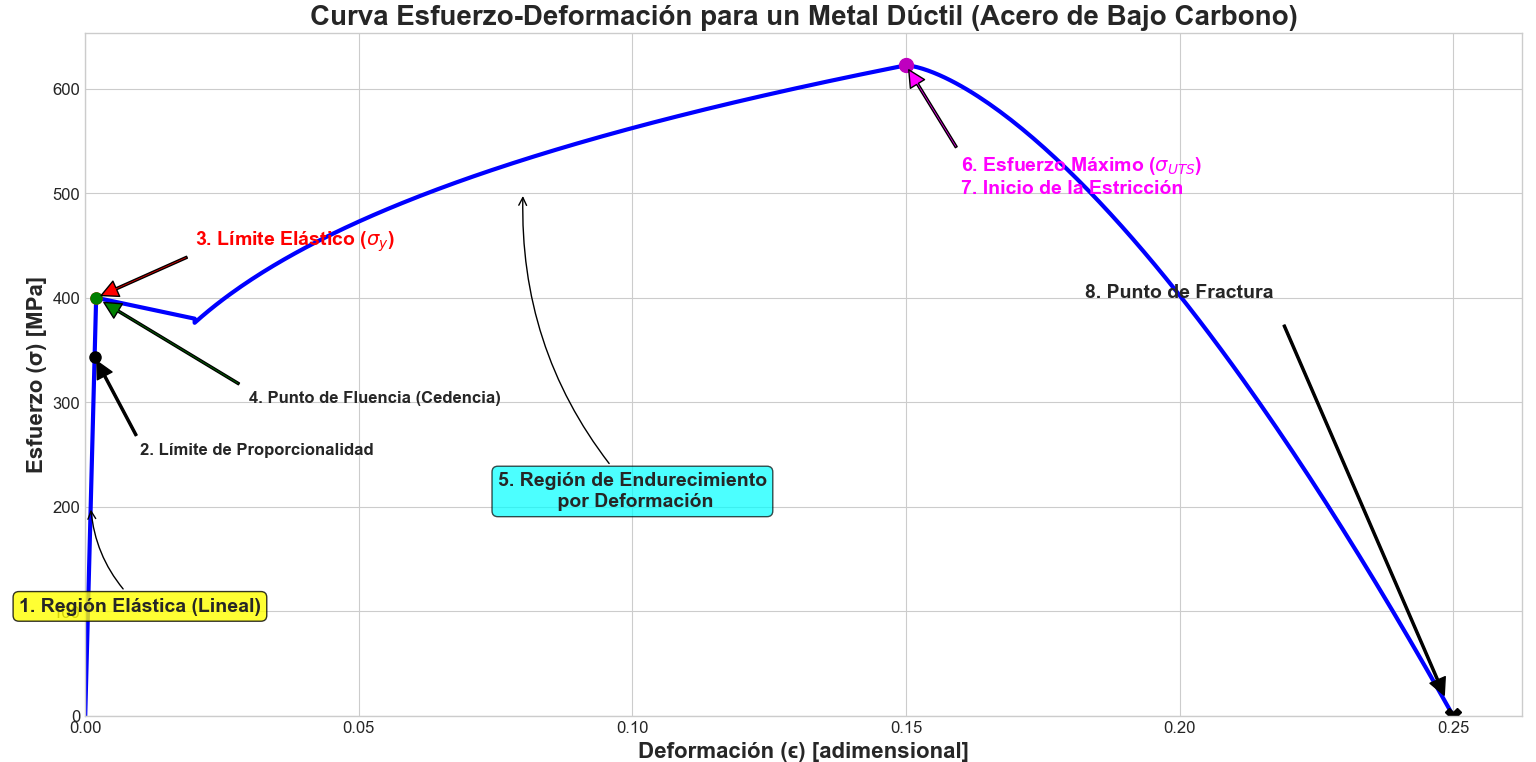
Veamos la Curva Esfuerzo-Deformación para un metal dúctil como el acero de bajo carbono.

Análisis de las Regiones y Puntos Clave

Analicemos paso a paso el viaje de un material a través de esta curva.

Región Elástica: Deformación Reversible

Esta es la primera porción de la curva, que a menudo es una línea recta.

• Límite de Proporcionalidad: Es el punto hasta el cual el esfuerzo es estrictamente proporcional a la deformación. La Ley de Hooke ($\sigma = E\epsilon$) es válida en esta zona.
• Límite Elástico (o Resistencia a la Fluencia, $\sigma_y$): Es el punto más crucial para el diseño elástico. Es el máximo esfuerzo que un material puede soportar sin sufrir una deformación permanente. Si la carga se retira antes de alcanzar este punto, el material volverá a su forma y tamaño originales, siguiendo la misma trayectoria lineal hacia abajo hasta el origen. Para la mayoría de los metales, el límite de proporcionalidad y el elástico están tan juntos que a menudo se consideran el mismo punto.

Región Plástica: Deformación Permanente

Una vez que se sobrepasa el límite elástico, el material entra en la región plástica.

• Fluencia o Cedencia: Es el fenómeno donde el material comienza a deformarse plásticamente. Algunos materiales, como el acero de bajo carbono, muestran un punto de fluencia muy definido, donde la deformación aumenta sin un incremento apreciable en el esfuerzo.
• Endurecimiento por Deformación (o Acritud): Después de la fluencia inicial, la curva vuelve a ascender. Esto significa que el material se vuelve más resistente y se necesita un esfuerzo mayor para continuar deformándolo. A nivel microscópico, esto se debe al movimiento y enredo de dislocaciones dentro de la estructura cristalina del material.

Esfuerzo Máximo y Fractura

• Resistencia Última a la Tracción ($\sigma_{UTS}$): Es el punto más alto de la curva de esfuerzo de ingeniería. Representa el máximo esfuerzo que el material puede soportar. Es una propiedad de resistencia clave.
• Estricción (o "Necking"): A partir del punto de esfuerzo máximo, la deformación comienza a concentrarse en una pequeña región de la probeta, causando una reducción significativa y localizada del área de la sección transversal. Este fenómeno se conoce como estricción. Debido a que el esfuerzo de ingeniería se calcula con el área inicial, la curva parece descender, aunque el esfuerzo real (o verdadero) en la zona de estricción sigue aumentando hasta la fractura.
• Fractura: Es el punto final de la curva, donde la probeta se rompe.

Propiedades Mecánicas Clave Obtenidas de la Curva

La curva esfuerzo-deformación es una mina de oro de información sobre las propiedades mecánicas de un material.

Rigidez

• Módulo de Young ($E$): Se determina a partir de la pendiente de la región elástica lineal. Un material con una pendiente pronunciada es muy rígido.

Resistencia

• Resistencia a la Fluencia ($\sigma_y$): Es el esfuerzo en el límite elástico. Es a menudo el criterio de diseño más importante para evitar que un componente se deforme permanentemente en servicio.
• Resistencia a la Tracción ($\sigma_{UTS}$): Es el esfuerzo máximo en la curva. Indica la máxima carga que una estructura puede soportar en condiciones de tracción.

Ductilidad

• Ductilidad: Es la capacidad de un material de deformarse plásticamente antes de fracturarse. Es una medida de cuánto "aviso" da un material antes de romperse. Se cuantifica principalmente de dos maneras:
  • Porcentaje de Alargamiento: $$ \% \text{Alargamiento} = \left(\frac{L_f - L_0}{L_0}\right) \times 100\% $$ Donde $L_f$ es la longitud final de la probeta después de la fractura.
  • Porcentaje de Reducción de Área: $$ \% \text{Reducción de Área} = \left(\frac{A_0 - A_f}{A_0}\right) \times 100\% $$ Donde $A_f$ es el área de la sección transversal final en el punto de fractura.

Tenacidad y Resiliencia

• Resiliencia: Es la capacidad de un material para absorber energía cuando se deforma elásticamente y liberarla cuando se retira la carga. Se cuantifica por el Módulo de Resiliencia, que es el área bajo la porción elástica de la curva esfuerzo-deformación.
• Tenacidad: Es la capacidad de un material para absorber energía y deformarse plásticamente antes de fracturarse. Se cuantifica por el área total bajo la curva esfuerzo-deformación. Un material tenaz (que combina buena resistencia y buena ductilidad) es deseable para aplicaciones que puedan sufrir cargas de impacto.

Comportamiento de Diferentes Tipos de Materiales

No todos los materiales siguen la curva "clásica" del acero dúctil. Su comportamiento puede variar drásticamente.

Materiales Dúctiles vs. Materiales Frágiles

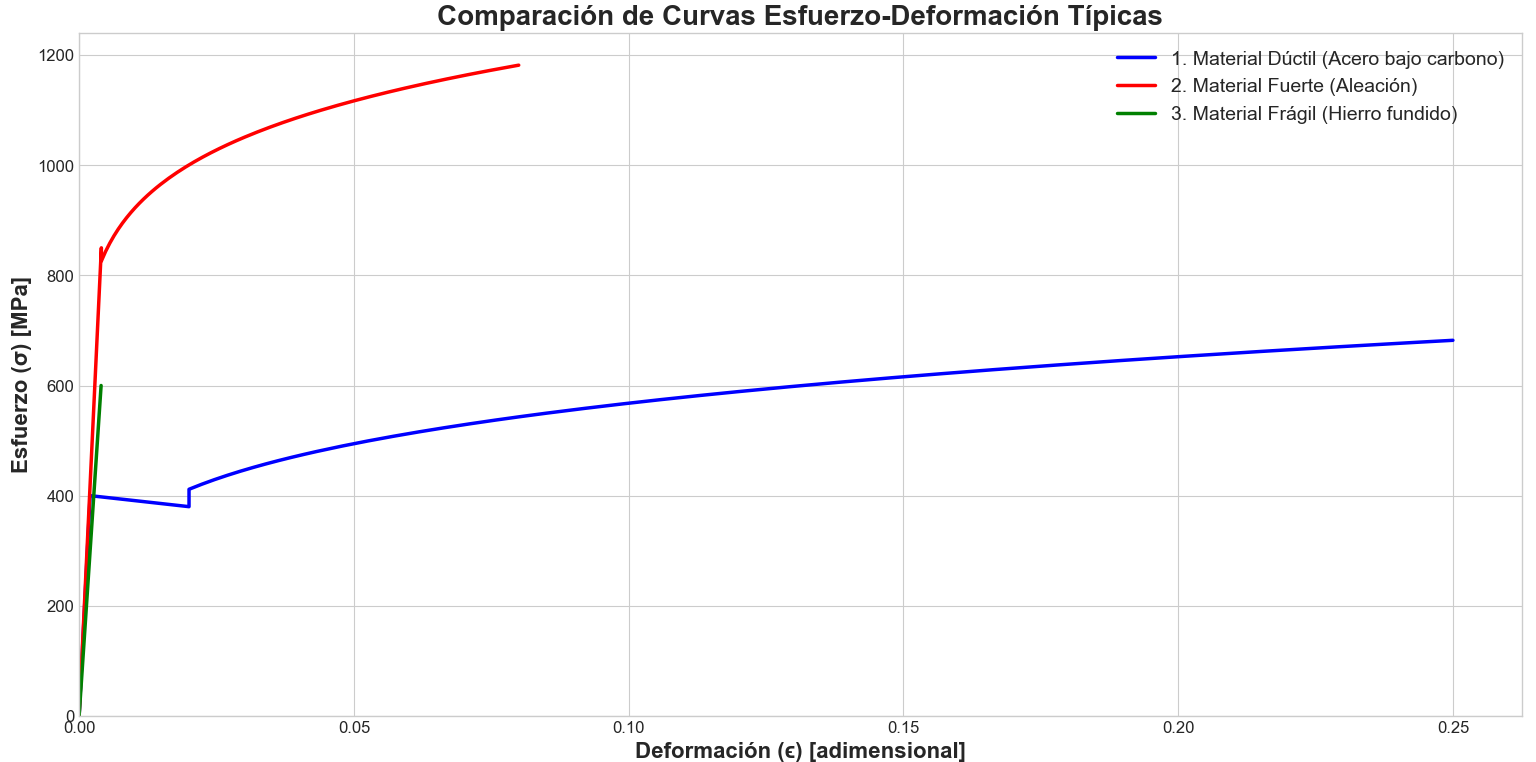
• Materiales Dúctiles: Como el acero, el aluminio o el cobre. Muestran una región plástica significativa, lo que les permite deformarse considerablemente antes de romperse. Este comportamiento proporciona una advertencia visual (flexión, abolladura) antes de una falla catastrófica.
• Materiales Frágiles: Como las cerámicas, el vidrio o el hierro fundido. Muestran muy poca o ninguna deformación plástica. La fractura ocurre de manera súbita y sin previo aviso poco después de superar el límite elástico.

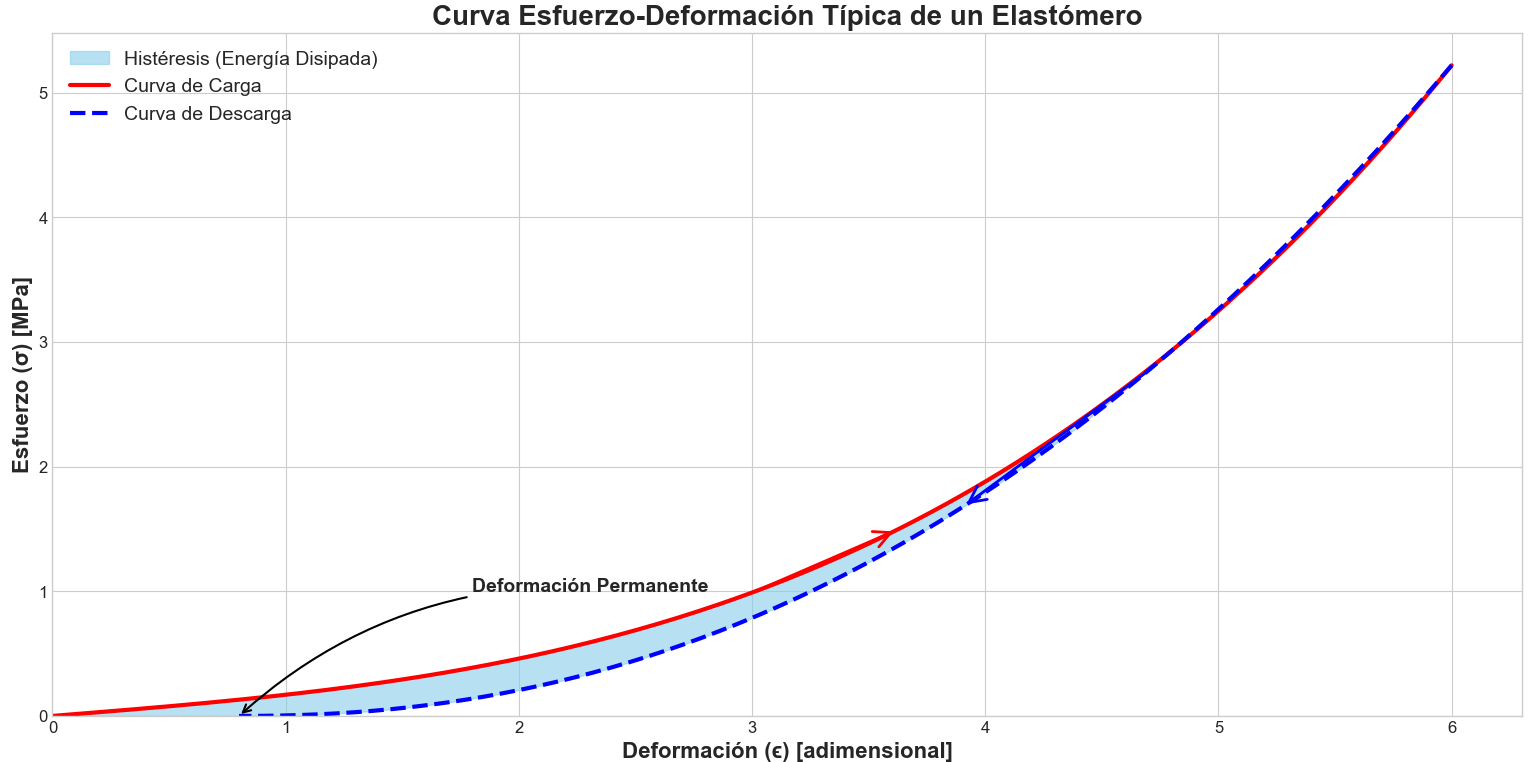
Elastómeros (Cauchos)

Los elastómeros, como el caucho, tienen un comportamiento muy diferente. Su curva esfuerzo-deformación es no lineal, incluso en la región elástica, y pueden soportar deformaciones enormes (varios cientos por ciento) y aun así volver a su forma original.

Ejercicios Resueltos de Límite Elástico y Curva de Esfuerzo - Deformación

Solución

▷ Paso 1 (a) Calcular el Módulo de Young ($E$).
$E$ es la pendiente de la región elástica lineal. Usando el origen ($0,0$) y el límite elástico ($\epsilon=0.002, \sigma=400 \text{ MPa}$):
$E = \frac{\Delta\sigma}{\Delta\epsilon} = \frac{400 \text{ MPa} - 0}{0.002 - 0} = \frac{400 \times 10^6 \text{ Pa}}{0.002} = 200 \times 10^9 \text{ Pa} = 200 \text{ GPa}$.

▷ Paso 2 (b) Identificar la resistencia a la fluencia ($\sigma_y$).
La resistencia a la fluencia (o límite elástico) es el esfuerzo en el que termina la región elástica. Según el gráfico, este punto es $\sigma_y = 400 \text{ MPa}$.

▷ Paso 3 (c) Identificar la resistencia a la tracción ($\sigma_{UTS}$).
La resistencia a la tracción es el valor máximo del esfuerzo en la curva. Según el gráfico, este punto es $\sigma_{UTS} = 700 \text{ MPa}$.

Respuesta:
a) El Módulo de Young es aproximadamente $200 \text{ GPa}$.
b) La resistencia a la fluencia es $400 \text{ MPa}$.
c) La resistencia a la tracción es $700 \text{ MPa}$.

Solución

▷ Paso 1 Analizar la deformación después del límite elástico.
El límite elástico ocurre a una deformación de $\epsilon = 0.002$. La fractura ocurre a $\epsilon = 0.25$.

▷ Paso 2 Justificar la clasificación.
El material experimenta una deformación plástica significativa (desde $0.002$ hasta $0.25$) antes de romperse. Esta gran capacidad de deformación plástica es la característica principal de un material dúctil. Un material frágil se rompería con una deformación muy cercana a la del límite elástico.

Respuesta: El material es dúctil, ya que muestra una gran región de deformación plástica antes de la fractura.

Solución

▷ Paso 1 Identificar los datos.
$L_0 = 50 \text{ mm}$.
$L_f = 62 \text{ mm}$.

▷ Paso 2 Aplicar la fórmula del porcentaje de alargamiento.
$\% \text{Alargamiento} = \left(\frac{L_f - L_0}{L_0}\right) \times 100\%$.
$\% \text{Alargamiento} = \left(\frac{62 \text{ mm} - 50 \text{ mm}}{50 \text{ mm}}\right) \times 100\%$.
$\% \text{Alargamiento} = \left(\frac{12}{50}\right) \times 100\% = 0.24 \times 100\%$.

Respuesta: El porcentaje de alargamiento es del $24\%$.

Solución

▷ Paso 1 Recordar la definición de tenacidad.
La tenacidad es la capacidad de absorber energía hasta la fractura y está representada por el área total bajo la curva esfuerzo-deformación.

▷ Paso 2 Comparar los materiales cualitativamente.
El material B tiene tanto una mayor resistencia (un valor de $\sigma_y$ más alto, y probablemente también un $\sigma_{UTS}$ más alto) como una ductilidad mucho mayor (deformación del $30\%$ frente al $5\%$).

▷ Paso 3 Concluir.
Dado que el área bajo la curva depende tanto de la altura (esfuerzo) como de la base (deformación), un material que tiene valores altos en ambas (especialmente una gran deformación hasta la fractura) absorberá mucha más energía. El material B, al ser más fuerte y mucho más dúctil, tendrá un área bajo la curva significativamente mayor que el material A.

Respuesta: El material B se consideraría más tenaz, ya que su combinación de alta resistencia y alta ductilidad le permite absorber mucha más energía antes de romperse.

Solución

▷ Paso 1 Identificar la región inicial de la curva.
La región inicial es la región elástica, que es lineal para la mayoría de los metales.

▷ Paso 2 Recordar la definición de la pendiente en esta región.
La pendiente de la curva $\sigma$ vs. $\epsilon$ es $\Delta\sigma/\Delta\epsilon$. Por la Ley de Hooke generalizada, $\sigma = E\epsilon$, por lo que $E = \sigma/\epsilon$.

Respuesta: La pendiente de la región elástica inicial de la curva esfuerzo-deformación representa el Módulo de Young ($E$) o Módulo de Elasticidad, que es una medida de la rigidez del material.

Solución

▷ Paso 1 Analizar el propósito del diseño.
El objetivo de un diseño seguro es que el componente funcione correctamente sin fallar. En la mayoría de las aplicaciones estructurales, la "falla" se define no solo como la rotura, sino también como cualquier deformación permanente que impida que el componente cumpla su función.

▷ Paso 2 Comparar las dos resistencias.
La resistencia a la fluencia ($\sigma_y$) es el umbral para la deformación permanente. Si el esfuerzo en el perno supera $\sigma_y$, el perno se estirará permanentemente y la unión podría aflojarse o fallar, aunque el perno no se haya roto. La resistencia a la tracción ($\sigma_{UTS}$) es el umbral para la rotura inminente.

▷ Paso 3 Concluir sobre el criterio de diseño.
Para evitar cualquier deformación permanente y garantizar la integridad funcional de la unión, el ingeniero debe asegurarse de que los esfuerzos de trabajo estén siempre por debajo de la resistencia a la fluencia, normalmente con un factor de seguridad. Por lo tanto, el diseño se basa principalmente en la resistencia a la fluencia.

Respuesta: El diseño debe basarse principalmente en la resistencia a la fluencia ($\sigma_y$). Superar este límite causa deformación permanente, lo que se considera una falla funcional en la mayoría de las aplicaciones, mucho antes de que se alcance la resistencia a la tracción y el perno se rompa.

Solución

▷ Paso 1 Dibujar la trayectoria de descarga.
La trayectoria de descarga no sigue la curva original hacia atrás. En cambio, sigue una línea recta hacia abajo, paralela a la pendiente elástica original.
(ingresar imagen: Una curva esfuerzo-deformación donde se muestra una carga que sube por la curva hasta un punto P en la región plástica. Desde el punto P, se dibuja una línea recta hacia abajo y hacia la izquierda, paralela a la pendiente elástica inicial, hasta que cruza el eje X ($\sigma=0$) en un punto de deformación positiva ($\epsilon_p$).)

▷ Paso 2 Describir lo que ha ocurrido.
Al retirar la carga, el material experimenta una recuperación elástica (la parte de la deformación que se recupera, correspondiente a la línea recta de descarga). Sin embargo, como el límite elástico fue superado, queda una deformación plástica permanente ($\epsilon_p$) cuando el esfuerzo llega a cero.

▷ Paso 3 Mencionar el efecto en las propiedades.
El material ahora es permanentemente más largo. Si se volviera a cargar, seguiría la línea de descarga hacia arriba y tendría un nuevo límite elástico más alto, cercano al punto P donde se detuvo la carga anterior. Este es el efecto del endurecimiento por deformación.

Respuesta: El material se descarga a lo largo de una línea paralela a su Módulo de Young original, dejando una deformación permanente. El material se ha vuelto más fuerte (mayor límite elástico) pero menos dúctil que en su estado original.

Solución

▷ Paso 1 Analizar la curva del material cerámico.
Una cerámica típica tiene un Módulo de Young muy alto (pendiente muy pronunciada) pero se fractura con muy poca deformación, justo después del límite elástico. Su curva es una línea casi recta y corta.
(Referirse a la imagen comparativa de materiales dúctiles y frágiles).

▷ Paso 2 Analizar la curva del acero dúctil.
El acero de bajo carbono tiene un Módulo de Young alto (aunque generalmente menor que el de la cerámica) y una enorme región de deformación plástica antes de la fractura. Su curva es alta y muy larga.

▷ Paso 3 Comparar la resiliencia.
La resiliencia es el área bajo la porción elástica. La cerámica, al tener un esfuerzo elástico alto y una pendiente pronunciada, puede tener una resiliencia comparable o incluso mayor que la del acero, ya que puede almacenar una cantidad significativa de energía elástica en su pequeña región de deformación.

▷ Paso 4 Comparar la tenacidad.
La tenacidad es el área total bajo la curva. El acero, con su inmensa región plástica, tiene un área total bajo la curva mucho, mucho mayor que la cerámica. La cerámica, al ser frágil, tiene un área total muy pequeña.

Respuesta: La resiliencia de la cerámica puede ser alta (capaz de almacenar energía elástica), pero su tenacidad es muy baja porque se rompe sin absorber mucha energía plástica. El acero de bajo carbono tiene una tenacidad extremadamente alta debido a su capacidad para deformarse plásticamente y absorber una gran cantidad de energía antes de fallar.

Conclusión

La curva esfuerzo-deformación es, sin duda, una de las herramientas más informativas en la ciencia e ingeniería de materiales. Nos proporciona una narrativa visual completa del comportamiento de un material bajo carga, llevándonos más allá del comportamiento elástico predecible y hacia los dominios de la deformación permanente y la fractura. Conceptos como el límite elástico, la resistencia a la tracción, la ductilidad y la tenacidad, todos extraídos de esta curva, son el lenguaje que usamos para seleccionar, diseñar y utilizar materiales de manera segura y eficaz.

Con este artículo, concluimos nuestro recorrido por los conceptos teóricos fundamentales de la elasticidad y las propiedades mecánicas. Hemos construido una base sólida que nos permitirá, en futuras publicaciones, abordar aplicaciones más complejas, analizar diferentes modos de falla y explorar el fascinante mundo de cómo los materiales dan forma a nuestra tecnología y nuestro entorno.