Módulo de Corte o Módulo de Cizalladura - Ejercicios Resueltos
Siguiendo nuestra serie sobre elasticidad, hemos explorado cómo los materiales responden a fuerzas que tienden a estirarlos o comprimirlos (descrito por el Módulo de Young) y la relación fundamental entre fuerza y deformación elástica (Ley de Hooke). Ahora, nos enfocaremos en cómo los materiales resisten cambios en su forma cuando se someten a fuerzas que intentan hacer deslizar una porción del material con respecto a otra. Esta propiedad es cuantificada por el Módulo de Corte ($G$), también conocido como Módulo de Cizalladura o Módulo de Rigidez.
Introducción
El Módulo de Corte ($G$) es una constante elástica que caracteriza la rigidez de un material frente a un esfuerzo cortante. Mientras que el Módulo de Young describe la resistencia de un material a cambiar su longitud (o volumen de forma indirecta bajo carga axial), el Módulo de Corte describe su resistencia a cambiar de forma sin cambiar de volumen. Imagina intentar deslizar la cubierta de un libro con respecto a sus páginas; la resistencia que sientes está relacionada con las propiedades de cizalladura del adhesivo y el papel. De manera similar, cuando un eje de transmisión se somete a torsión o un perno se somete a fuerzas de corte, el Módulo de Corte del material es el que determina cuánta deformación angular ocurrirá. ¿se entiende?

Comprender el Módulo de Corte es crucial para el diseño de una amplia variedad de componentes y estructuras mecánicas, como ejes, árboles de transmisión, resortes de torsión, uniones atornilladas o remachadas, y en el análisis de la estabilidad de materiales bajo cargas complejas. Este post definirá el Módulo de Corte, explicará cómo se relaciona con el esfuerzo y la deformación por cizalladura, cómo se determina y cuáles son sus aplicaciones prácticas.
Definición del Módulo de Corte ($G$)
Para entender el Módulo de Corte, es esencial recordar los conceptos de esfuerzo cortante y deformación unitaria por cizalladura, introducidos en el primer artículo de esta serie. Si tienes dudas, y quieres leer el artículo completo 👇
Recordando Esfuerzo Cortante ($\tau$) y Deformación Unitaria por Cizalladura ($\gamma$)
El esfuerzo cortante ($\tau$) se define como la fuerza ($F_{\parallel}$) que actúa paralela a una superficie, dividida por el área ($A$) de esa superficie:
$$\tau = \frac{F_{\parallel}}{A}$$
La deformación unitaria por cizalladura ($\gamma$) es una medida de la distorsión angular producida por el esfuerzo cortante. Para ángulos pequeños, se define como el desplazamiento tangencial ($x$) de una cara del elemento dividido por su altura ($h$) perpendicular a esa cara, o como el ángulo de distorsión $\theta$ (en radianes):
$$\gamma \approx \tan\theta \approx \theta = \frac{x}{h}$$
El Módulo de Corte como Constante de Proporcionalidad
De forma análoga a la Ley de Hooke para esfuerzos normales ($\sigma = E\epsilon$), existe una relación lineal entre el esfuerzo cortante y la deformación unitaria por cizalladura para materiales elásticos dentro de su límite de proporcionalidad:
$$\tau = G\gamma$$
El Módulo de Corte ($G$) es la constante de proporcionalidad en esta relación. Por lo tanto, se define como la relación entre el esfuerzo cortante y la deformación unitaria por cizalladura:
$$G = \frac{\text{Esfuerzo Cortante}}{\text{Deformación Unitaria por Cizalladura}} = \frac{\tau}{\gamma}$$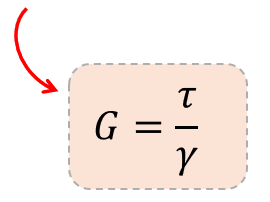
Las unidades del Módulo de Corte en el Sistema Internacional son las mismas que las del esfuerzo y el Módulo de Young: Pascales (Pa) o Newtons por metro cuadrado ($N/m^2$). También se utilizan comúnmente los Megapascales (MPa) y Gigapascales (GPa). A veces se le denomina Módulo de Rigidez.
[alert-note] Ejemplo Un bloque de un material se somete a un esfuerzo cortante de $\tau = 25 \text{ MPa}$ y experimenta una deformación unitaria por cizalladura de $\gamma = 0.0005 \text{ rad}$. ¿Cuál es su Módulo de Corte? [/alert-note]
Solución:
Primero, convertimos el esfuerzo a Pascales: $\tau = 25 \text{ MPa} = 25 \times 10^6 \text{ Pa}$.
$\displaystyle G=\frac{\tau }{\gamma }=\frac{{25\times {{{10}}^{6}}\text{ Pa}}}{{0.0005}}$
$\displaystyle G=\frac{{25\times {{{10}}^{6}}\text{ Pa}}}{{5\times {{{10}}^{{-4}}}}}=5\times {{10}^{{10}}}\text{ Pa}=50\times {{10}^{9}}\text{ Pa}$
\[ \boxed{G = 50\,\text{GPa}} \]
Significado Físico del Módulo de Corte
El Módulo de Corte ($G$) cuantifica la resistencia de un material a cambiar de forma (distorsión angular) cuando se aplican fuerzas cortantes, sin que haya un cambio en su volumen (para materiales isótropos y deformaciones puramente por cizalladura).
- Un valor alto de $G$ indica que el material es muy rígido a la cizalladura o torsión; es decir, se necesita un gran esfuerzo cortante para producir una pequeña distorsión angular.
- Un valor bajo de $G$ indica que el material es poco resistente a la cizalladura y se deforma angularmente con relativa facilidad.
Por ejemplo, los metales suelen tener módulos de corte altos, mientras que los elastómeros (como el caucho) tienen módulos de corte muy bajos.
Determinación Experimental y Valores Típicos
El Módulo de Corte, al igual que el Módulo de Young, es una propiedad intrínseca del material que se determina mediante ensayos experimentales.
Ensayo de Torsión
Un método común para determinar el Módulo de Corte es el ensayo de torsión. En este ensayo, se aplica un par de torsión (torque, $T$) a una muestra cilíndrica (o tubular) del material y se mide el ángulo de giro ($\phi$) resultante sobre una longitud conocida ($L$) de la muestra.

A partir del par de torsión aplicado, las dimensiones de la muestra y el ángulo de giro, se pueden calcular el esfuerzo cortante máximo ($\tau_{max}$) en la superficie de la muestra y la deformación unitaria por cizalladura correspondiente ($\gamma_{max}$). La relación entre estos, en la región elástica lineal, da el Módulo de Corte: $G = \tau_{max} / \gamma_{max}$.
Valores del Módulo de Corte para Diversos Materiales
El Módulo de Corte ($G$) es generalmente menor que el Módulo de Young ($E$) para el mismo material. Para muchos metales isótropos, $G$ suele estar en el rango de $0.3E$ a $0.4E$. Los valores específicos dependen de la composición y microestructura del material.
| Material | Módulo de Young \( E \) (GPa) | Módulo de Corte \( G \) (GPa) |
|---|---|---|
| Acero (estructural) | \( E \approx 200 \, \text{GPa} \) | \( G \approx 77 \text{–} 80 \, \text{GPa} \) |
| Aluminio (aleaciones) | \( E \approx 70 \, \text{GPa} \) | \( G \approx 26 \, \text{GPa} \) |
| Cobre | \( E \approx 120 \, \text{GPa} \) | \( G \approx 45 \, \text{GPa} \) |
| Titanio (aleaciones) | \( E \approx 110 \, \text{GPa} \) | \( G \approx 41 \, \text{GPa} \) |
| Vidrio (común) | \( E \approx 70 \, \text{GPa} \) | \( G \approx 29 \, \text{GPa} \) |
📝 Nota: Estos son valores aproximados y pueden variar.
[alert-note] Ejemplo El acero estructural tiene un Módulo de Young $E \approx 200 \text{ GPa}$. Usando la aproximación $G \approx 0.4E$, estimar su Módulo de Corte. [/alert-note]
Solución:
$G_{acero} \approx 0.4 \times (200 \text{ GPa}) = 80 \text{ GPa}$.
Este valor estimado es consistente con los valores tabulados típicos para el acero.
Relación entre Módulos Elásticos para Materiales Isótropos
Para materiales isótropos (aquellos cuyas propiedades son las mismas en todas las direcciones), los módulos elásticos como el Módulo de Young ($E$), el Módulo de Corte ($G$), el Módulo Volumétrico ($K$) y el Coeficiente de Poisson ($\nu$) no son completamente independientes entre sí.
Interdependencia de $E$, $G$ y $\nu$
Existe una relación matemática que vincula $E$, $G$ y el Coeficiente de Poisson ($\nu$). El Coeficiente de Poisson, que describiremos en detalle en un próximo artículo, es la relación entre la deformación unitaria transversal y la deformación unitaria axial. La relación es:
$$E = 2G(1+\nu)$$
Esta ecuación implica que si se conocen dos de estas tres constantes elásticas para un material isótropo, la tercera puede ser calculada. Por ejemplo, a menudo es más fácil medir $E$ (mediante ensayo de tracción) y $\nu$, y luego calcular $G$.
[alert-note] Ejemplo Un material tiene un Módulo de Young $E = 180 \text{ GPa}$ y un Coeficiente de Poisson $\nu = 0.28$. Calcula su Módulo de Corte $G$.[/alert-note]
De la fórmula $E = 2G(1+\nu)$, despejamos $G$:
$G = \frac{E}{2(1+\nu)}$
$G = \frac{180 \text{ GPa}}{2(1+0.28)} = \frac{180 \text{ GPa}}{2(1.28)} = \frac{180 \text{ GPa}}{2.56} \approx 70.31 \text{ GPa}$.
Aplicaciones del Módulo de Corte
El Módulo de Corte es fundamental en diversas aplicaciones de ingeniería donde los materiales están sujetos a cizalladura o torsión.
Diseño de Ejes y Elementos Sometidos a Torsión
Los ejes que transmiten potencia (como los ejes de motores o cajas de cambios) están sometidos a pares de torsión, lo que induce esfuerzos cortantes. El Módulo de Corte se utiliza para calcular el ángulo de giro ($\phi$) de un eje bajo un par de torsión ($T$) dado:
$$\phi = \frac{TL}{GJ}$$
Donde $L$ es la longitud del eje y $J$ es el momento polar de inercia de la sección transversal del eje. Es crucial para asegurar que la deformación torsional no sea excesiva.
Análisis de Uniones (Pernos, Remaches, Soldaduras)
Los elementos de unión como pernos, remaches y cordones de soldadura a menudo están sometidos a fuerzas cortantes. El Módulo de Corte del material de estos elementos es importante para analizar su comportamiento y asegurar que no fallen por cizalladura.
Resortes de Torsión y Barras de Torsión en Suspensiones
Muchos tipos de resortes, como los resortes de torsión (utilizados en pinzas de ropa o trampas para ratones) o las barras de torsión (utilizadas en las suspensiones de algunos vehículos), funcionan gracias a la deformación elástica por cizalladura del material. El Módulo de Corte es esencial para su diseño.
Ejercicios Resueltos de Módulo de Corte
Solución
▷ Paso 1 Identificar los datos y convertir unidades.
$\gamma = 0.0012 \text{ rad}$.
$\tau = 60 \text{ MPa} = 60 \times 10^6 \text{ Pa}$.
▷ Paso 2 Aplicar la fórmula $G = \frac{\tau}{\gamma}$.
$G = \frac{60 \times 10^6 \text{ Pa}}{0.0012} = \frac{60 \times 10^6 \text{ Pa}}{1.2 \times 10^{-3}}$.
$G = \frac{60}{1.2} \times 10^9 \text{ Pa} = 50 \times 10^9 \text{ Pa}$.
▷ Paso 3 Expresar el resultado en Gigapascales (GPa).
$G = 50 \text{ GPa}$.
Respuesta: El Módulo de Corte del material es $50 \text{ GPa}$.
Solución
▷ Paso 1 Identificar los datos.
$\gamma = 0.0008 \text{ rad}$.
$G = 75 \text{ GPa} = 75 \times 10^9 \text{ Pa}$.
▷ Paso 2 Aplicar la fórmula $\tau = G\gamma$.
$\tau = (75 \times 10^9 \text{ Pa}) \times (0.0008)$.
$\tau = (75 \times 10^9) \times (8 \times 10^{-4}) \text{ Pa}$.
$\tau = 600 \times 10^5 \text{ Pa} = 60 \times 10^6 \text{ Pa}$.
▷ Paso 3 Expresar el resultado en Megapascales (MPa).
$\tau = 60 \text{ MPa}$.
Respuesta: Se necesita un esfuerzo cortante de $60 \text{ MPa}$.
Solución
▷ Paso 1 Calcular el área de la sección transversal ($A$) del perno.
Diámetro $d = 10 \text{ mm} = 0.01 \text{ m}$. Radio $r = 0.005 \text{ m}$.
$A = \pi r^2 = \pi (0.005 \text{ m})^2 = \pi (2.5 \times 10^{-5} \text{ m}^2) \approx 7.854 \times 10^{-5} \text{ m}^2$.
▷ Paso 2 Calcular el esfuerzo cortante ($\tau$).
Fuerza $F_{\parallel} = 5 \text{ kN} = 5000 \text{ N}$.
$\tau = \frac{F_{\parallel}}{A} = \frac{5000 \text{ N}}{7.854 \times 10^{-5} \text{ m}^2} \approx 63.66 \times 10^6 \text{ Pa} = 63.66 \text{ MPa}$.
▷ Paso 3 Calcular la deformación unitaria por cizalladura ($\gamma = \tau/G$).
$G = 80 \text{ GPa} = 80 \times 10^9 \text{ Pa}$.
$\gamma = \frac{63.66 \times 10^6 \text{ Pa}}{80 \times 10^9 \text{ Pa}} = \frac{63.66}{80000} \approx 0.0007957 \text{ rad}$.
Respuesta: La deformación unitaria por cizalladura en el perno es aproximadamente $0.000796 \text{ rad}$.
Solución
▷ Paso 1 Identificar los datos.
$E = 200 \text{ GPa}$.
$\nu = 0.3$.
▷ Paso 2 Aplicar la fórmula $G = \frac{E}{2(1+\nu)}$.
$G = \frac{200 \text{ GPa}}{2(1+0.3)} = \frac{200 \text{ GPa}}{2(1.3)} = \frac{200 \text{ GPa}}{2.6}$.
▷ Paso 3 Calcular el valor de $G$.
$G \approx 76.92 \text{ GPa}$.
Respuesta: El Módulo de Corte del material es aproximadamente $76.92 \text{ GPa}$.
Solución
▷ Paso 1 Identificar los datos.
$\tau_{max} = 45 \text{ MPa} = 45 \times 10^6 \text{ Pa}$.
$G = 30 \text{ GPa} = 30 \times 10^9 \text{ Pa}$.
(La longitud y el radio no son necesarios para esta pregunta específica, pero serían útiles para calcular el ángulo de giro o el par de torsión).
▷ Paso 2 Aplicar la fórmula $G = \tau/\gamma$ para despejar $\gamma$.
$\gamma_{max} = \frac{\tau_{max}}{G}$.
▷ Paso 3 Calcular $\gamma_{max}$.
$\gamma_{max} = \frac{45 \times 10^6 \text{ Pa}}{30 \times 10^9 \text{ Pa}} = \frac{45}{30000} = \frac{1.5}{1000} = 0.0015 \text{ rad}$.
Respuesta: La deformación unitaria por cizalladura máxima en la superficie del eje es $0.0015 \text{ rad}$.
a) El esfuerzo cortante.
b) La deformación unitaria por cizalladura.
c) El Módulo de Corte del material.
Solución
▷ Paso 1 (a) Calcular el área de la cara superior (área sometida a cizalladura).
Lado $= 10 \text{ cm} = 0.1 \text{ m}$.
$A = (0.1 \text{ m}) \times (0.1 \text{ m}) = 0.01 \text{ m}^2$ (asumiendo que la fuerza se distribuye sobre el lado de $10 \text{ cm} \times 10 \text{ cm}$ que es la cara superior. El espesor no se usa para el área de cizalladura en este caso, sino la altura para la deformación).
Fuerza $F_{\parallel} = 1500 \text{ N}$.
$\tau = \frac{F_{\parallel}}{A} = \frac{1500 \text{ N}}{0.01 \text{ m}^2} = 150000 \text{ Pa} = 0.15 \text{ MPa}$.
▷ Paso 2 (b) Calcular la deformación unitaria por cizalladura.
Desplazamiento $x = 0.03 \text{ mm} = 0.03 \times 10^{-3} \text{ m}$.
Altura $h = 10 \text{ cm} = 0.1 \text{ m}$ (asumiendo que la altura sobre la que ocurre el desplazamiento es el lado de la placa, si la fuerza se aplica a una cara de $10 \text{ cm} \times 1 \text{ cm}$ y la altura es el otro $10 \text{ cm}$. O si la fuerza es sobre la cara $10 \text{ cm} \times 10 \text{ cm}$ y la "altura" de cizalladura es el espesor $1 \text{ cm}$. El problema es ambiguo. Asumiremos que la "altura" para la deformación es $h=10 \text{ cm}$ si la fuerza actúa en la cara $10\text{cm} \times 1\text{cm}$ o si la fuerza actúa sobre una cara $10\text{cm} \times 10\text{cm}$ y la altura de cizalladura es $1\text{cm}$. Vamos a asumir que la fuerza se aplica a la cara de $10 \text{cm} \times 1 \text{cm}$ y la altura sobre la que se cizalla es $10 \text{cm}$. No, es más lógico que la fuerza actúe sobre una cara $10 \text{cm} \times 10 \text{cm}$ y la altura sea el espesor $1 \text{cm}$ o que la fuerza se aplique a una cara $10 \text{cm} \times 1 \text{cm}$ y la altura sea $10 \text{cm}$.
Reinterpretación: "placa cuadrada de $10 \text{ cm}$ de lado y $1 \text{ cm}$ de espesor... fija en su base. Se aplica una fuerza horizontal de $1500 \text{ N}$ a su cara superior, paralela a esta." La "cara superior" sería $10 \text{cm} \times 10 \text{cm}$. El área de cizalladura $A = (0.1\text{m})^2 = 0.01 \text{m}^2$. La "altura" $h$ sobre la cual ocurre el gradiente de desplazamiento es el espesor $1 \text{cm} = 0.01 \text{m}$.
(Re-cálculo para (a) y (b) basado en esta interpretación)
Área $A = (0.1 \text{ m}) \times (0.1 \text{ m}) = 0.01 \text{ m}^2$ (área de la cara superior)
$\tau = \frac{1500 \text{ N}}{0.01 \text{ m}^2} = 150000 \text{ Pa} = 0.15 \text{ MPa}$. (Esto permanece igual)
Altura $h = 1 \text{ cm} = 0.01 \text{ m}$ (espesor de la placa, sobre el cual ocurre la cizalladura).
$\gamma = \frac{x}{h} = \frac{0.03 \times 10^{-3} \text{ m}}{0.01 \text{ m}} = \frac{0.03 \times 10^{-3}}{1 \times 10^{-2}} = 0.03 \times 10^{-1} = 0.003 \text{ rad}$.
▷ Paso 3 (c) Calcular el Módulo de Corte.
$G = \frac{\tau}{\gamma} = \frac{150000 \text{ Pa}}{0.003 \text{ rad}} = \frac{150 \times 10^3}{3 \times 10^{-3}} \text{ Pa} = 50 \times 10^6 \text{ Pa} = 50 \text{ MPa}$.
Respuesta:
a) El esfuerzo cortante es $0.15 \text{ MPa}$.
b) La deformación unitaria por cizalladura es $0.003 \text{ rad}$.
c) El Módulo de Corte del material es $50 \text{ MPa}$.
Solución
▷ Paso 1 Identificar los datos.
$G = 25 \text{ GPa}$.
$\nu = 0.35$.
▷ Paso 2 Aplicar la fórmula $E = 2G(1+\nu)$.
$E = 2 \times (25 \text{ GPa}) \times (1+0.35)$.
$E = 50 \text{ GPa} \times (1.35)$.
▷ Paso 3 Calcular el valor de $E$.
$E = 67.5 \text{ GPa}$.
Respuesta: El Módulo de Young del material es $67.5 \text{ GPa}$.
Solución
▷ Paso 1 Identificar datos y convertir unidades.
$L = 1.5 \text{ m}$.
$G = 26 \text{ GPa} = 26 \times 10^9 \text{ Pa}$.
$T = 800 \text{ N} \cdot \text{m}$.
Radio exterior $R = 60\text{mm}/2 = 30 \text{ mm} = 0.03 \text{ m}$.
Radio interior $r = 40\text{mm}/2 = 20 \text{ mm} = 0.02 \text{ m}$.
▷ Paso 2 Calcular el momento polar de inercia ($J$).
$J = \frac{\pi}{2}(R^4 - r^4) = \frac{\pi}{2}((0.03 \text{ m})^4 - (0.02 \text{ m})^4)$.
$R^4 = (3 \times 10^{-2})^4 = 81 \times 10^{-8} \text{ m}^4$.
$r^4 = (2 \times 10^{-2})^4 = 16 \times 10^{-8} \text{ m}^4$.
$J = \frac{\pi}{2}(81 \times 10^{-8} - 16 \times 10^{-8}) \text{ m}^4 = \frac{\pi}{2}(65 \times 10^{-8}) \text{ m}^4$.
$J \approx \frac{3.14159}{2} \times 65 \times 10^{-8} \text{ m}^4 \approx 1.5708 \times 65 \times 10^{-8} \text{ m}^4 \approx 102.102 \times 10^{-8} \text{ m}^4 = 1.021 \times 10^{-6} \text{ m}^4$.
▷ Paso 3 Aplicar la fórmula del ángulo de giro ($\phi = \frac{TL}{GJ}$).
$\phi = \frac{(800 \text{ N} \cdot \text{m})(1.5 \text{ m})}{(26 \times 10^9 \text{ N/m}^2)(1.021 \times 10^{-6} \text{ m}^4)}$.
$\phi = \frac{1200}{26 \times 1.021 \times 10^3} \text{ rad}$.
$\phi = \frac{1200}{26546} \text{ rad} \approx 0.04520 \text{ rad}$.
▷ Paso 4 (Opcional) Convertir el ángulo a grados.
$\phi \text{ (grados)} = 0.04520 \text{ rad} \times \frac{180^\circ}{\pi \text{ rad}} \approx 0.04520 \times 57.2958^\circ \approx 2.59_0^\circ$.
Respuesta: El ángulo de giro total del tubo es aproximadamente $0.0452 \text{ rad}$ o $2.59^\circ$.
Conclusión
El Módulo de Corte ($G$), o Módulo de Rigidez, es una propiedad fundamental que describe la resistencia de un material a cambiar de forma bajo la acción de fuerzas cortantes o de torsión, sin cambiar su volumen. Hemos visto que se define como la relación entre el esfuerzo cortante y la deformación unitaria por cizalladura, $G = \tau/\gamma$, y es una medida directa de la rigidez del material frente a este tipo de solicitaciones.
Su conocimiento es indispensable en el diseño de componentes sometidos a torsión, como ejes de transmisión, y en el análisis de uniones y elementos estructurales que experimentan cizalladura. Además, hemos introducido brevemente su relación con el Módulo de Young y el Coeficiente de Poisson para materiales isótropos, destacando la interconexión de las constantes elásticas. En los próximos artículos, continuaremos explorando estas relaciones y otras constantes elásticas importantes, como el Módulo Volumétrico y el Coeficiente de Poisson, para obtener una comprensión aún más completa de la elasticidad de los materiales.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar