Conceptos Clave: Población, Muestra y Variable Estadística

¡Hola, futuro genio de los datos! 🤠 ¿Alguna vez te has preguntado cómo Netflix sabe qué series recomendarte, cómo los científicos predicen el clima o cómo las empresas deciden lanzar un nuevo producto? La respuesta, en gran medida, se encuentra en el fascinante mundo de la Probabilidad y la Estadística. Lejos de ser un conjunto de fórmulas aburridas, es una poderosa herramienta para entender la realidad, descubrir patrones ocultos y tomar decisiones inteligentes basadas en evidencia. En este artículo, vamos a desglosar los tres pilares sobre los que se construye todo el edificio de la estadística: la población, la muestra y la variable estadística. ¡Prepárate para un viaje que cambiará tu forma de ver el mundo! 🚀

Entendiendo el Corazón de la Estadística: ¿Para Qué Sirve?

Antes de sumergirnos en los conceptos clave, demos un paso atrás. La estadística es la ciencia que se ocupa de recolectar, organizar, analizar, interpretar y presentar datos. Su objetivo es transformar un mar de números y observaciones en conocimiento útil. Se divide principalmente en dos grandes ramas:

• Estadística Descriptiva: Se enfoca en resumir y describir las características de un conjunto de datos. Piensa en ella como la fotografía de tus datos: te muestra el promedio, la moda, la mediana, la desviación estándar, etc. Su finalidad es darnos una idea clara y concisa de lo que tenemos entre manos.
• Estadística Inferencial: Aquí es donde ocurre la magia. Esta rama utiliza los datos de un grupo pequeño para hacer generalizaciones, predicciones o inferencias sobre un grupo mucho más grande. Es como probar una cucharada de sopa para saber si a toda la olla le falta sal.

Para poder hacer tanto una buena descripción como una inferencia precisa, necesitamos entender de dónde vienen nuestros datos y qué estamos midiendo. Y aquí es donde entran en juego nuestros tres protagonistas de hoy.

Población Estadística: El Universo de Nuestros Datos 🌎

En nuestra vida cotidiana, la palabra "población" nos hace pensar en el número de habitantes de una ciudad o un país. En estadística, el concepto es mucho más amplio y flexible. Es el punto de partida de cualquier estudio.

Es crucial definir la población con total claridad al inicio de cualquier investigación, ya que los resultados del estudio se aplicarán a ella. Las poblaciones se pueden clasificar en dos tipos principales:

Población Finita

Es aquella cuyo número de elementos es contable o se puede enumerar. Aunque sea un número muy grande, es limitado. Por ejemplo:

• Todos los estudiantes matriculados en una universidad específica este semestre.
• El número de coches fabricados por una planta en un año.
• La totalidad de los libros en la Biblioteca Nacional.

Aunque teóricamente podríamos acceder a cada uno de los miembros, en la práctica puede ser extremadamente costoso y lento.

Población Infinita

Es aquella cuyo número de elementos es ilimitado o tan grande que, para fines prácticos, se considera infinito. A menudo, estas poblaciones están asociadas a procesos continuos.

• El conjunto de todas las posibles mediciones de presión arterial de una persona a lo largo de su vida.
• Todos los posibles lanzamientos de un dado. Teóricamente, podrías seguir lanzándolo por siempre.
• El conjunto de todas las piezas que una máquina podría producir si funcionara ininterrumpidamente.

Ahora, imagina que eres un ingeniero de calidad y quieres verificar la vida útil de una nueva línea de bombillas LED. Tu población son todas las bombillas producidas y por producir con esa tecnología. ¿Sería práctico probar cada una de ellas hasta que se funda? ¡Claro que no! Te quedarías sin bombillas para vender. Este dilema nos lleva directamente al siguiente concepto clave.

Muestra Estadística: Una Ventana a la Población 🖼️

Dado que estudiar a toda la población es a menudo imposible o impracticable, los estadísticos recurren a una solución ingeniosa: estudiar un subconjunto representativo de ella. A este subconjunto lo llamamos muestra.

La calidad de nuestras inferencias dependerá directamente de la calidad de nuestra muestra. Si la muestra está sesgada (es decir, no es representativa), nuestras conclusiones serán erróneas, por muy sofisticado que sea nuestro análisis. Por ejemplo, si queremos saber la intención de voto para las próximas elecciones y solo encuestamos a universitarios, nuestra muestra estaría sesgada y no representaría a toda la población votante.

Para garantizar la representatividad, se han desarrollado diversas técnicas de muestreo. La más conocida es el muestreo aleatorio simple, donde cada miembro de la población tiene exactamente la misma probabilidad de ser seleccionado. Otras técnicas incluyen el muestreo estratificado, por conglomerados y sistemático, cada uno adaptado a diferentes situaciones.

Solución:

En este caso, la estrategia estadística es la siguiente:

• Población: Los 10,000 tornillos que componen un lote de producción. Es una población finita.
• Muestra: El equipo de calidad decide seleccionar aleatoriamente 200 tornillos de cada lote para medirlos. Estos 200 tornillos constituyen la muestra.
• Inferencia: Si el diámetro promedio y la variabilidad de los 200 tornillos de la muestra están dentro de las especificaciones, se infiere que todo el lote de 10,000 tornillos es de buena calidad y se aprueba para su envío. Si no, se rechaza el lote completo para una inspección más detallada.

Variable Estadística: La Característica que Medimos 📏

Ya tenemos nuestra población y hemos seleccionado una muestra. Pero, ¿qué es exactamente lo que vamos a medir o registrar de cada elemento? Esa característica de interés es lo que llamamos variable estadística.

En el ejemplo de los tornillos, la variable que nos interesa es el "diámetro". En un estudio sobre estudiantes, las variables podrían ser "edad", "género", "calificación en matemáticas" o "carrera que estudia". El tipo de variable es fundamental, ya que determina el tipo de análisis estadístico que podemos realizar. Las variables se dividen en dos grandes grupos.

Variables Cualitativas (o Categóricas)

Describen una cualidad o característica. Sus valores no son numéricos, sino categorías o nombres. No podemos realizar operaciones aritméticas con ellas. Se subdividen en:

• Nominales: Son categorías que no tienen un orden o jerarquía intrínseca. Simplemente nombran o clasifican.
  • Ejemplos: Género (masculino, femenino, otro), estado civil (soltero, casado, divorciado), tipo de sangre (A, B, AB, O), color de ojos (azul, verde, marrón).
• Ordinales: Son categorías que sí pueden ser ordenadas o jerarquizadas, pero la diferencia entre ellas no es cuantificable o uniforme.
  • Ejemplos: Nivel de satisfacción (muy insatisfecho, insatisfecho, neutral, satisfecho, muy satisfecho), nivel educativo (primaria, secundaria, universidad, postgrado), clasificación en una carrera (primer lugar, segundo lugar, tercer lugar).

Variables Cuantitativas (o Numéricas)

Son aquellas cuyos valores se expresan mediante números. Con ellas sí podemos realizar operaciones aritméticas como sumar o calcular promedios. Se subdividen en:

• Discretas: Toman valores numéricos enteros y aislados. Generalmente, provienen de un proceso de conteo. No puede haber valores intermedios entre dos valores consecutivos.
  • Ejemplos: Número de hijos en una familia (0, 1, 2, 3...), número de correos electrónicos recibidos en una hora, cantidad de defectos en un lote de productos.
• Continuas: Pueden tomar cualquier valor numérico dentro de un rango determinado. Generalmente, provienen de un proceso de medición. Teóricamente, entre dos valores siempre puede existir un valor intermedio.
  • Ejemplos: Altura de una persona (1.75 m, 1.751 m, 1.7512 m...), temperatura de una habitación, peso de un objeto, tiempo que se tarda en completar una tarea.

Ejemplos Guiados: Poniendo la Teoría en Práctica 💡

Vamos a solidificar estos conceptos identificando la población, la muestra y las variables en algunos escenarios del mundo real.

Solución:

• Población: Los 25 millones de votantes registrados en el país.
• Muestra: Las 1,200 personas que fueron contactadas y respondieron la encuesta.
• Variables:
  1. Candidato preferido: Es una variable cualitativa nominal. Los valores son nombres de candidatos (Candidato A, Candidato B, etc.) y no hay un orden inherente entre ellos.
  2. Rango de edad: (e.g., 18-25, 26-40, 41-60, +60). Esta es una variable cualitativa ordinal. Hay un orden claro en las categorías, pero la "distancia" entre "18-25" y "26-40" no es un número con el que se pueda operar directamente. Si hubieran preguntado la edad exacta (e.g., 23 años), sería cuantitativa.
  3. Nivel de ingresos anual: Es una variable cuantitativa continua, ya que los ingresos pueden tomar cualquier valor dentro de un rango (e.g., $35,450.75).

Solución:

• Población: Todos los arrecifes de coral dentro de la reserva natural de 150 km².
• Muestra: Las 10 áreas de 1 km² que fueron seleccionadas para el estudio.
• Variables:
  1. Número de especies de peces: Es una variable cuantitativa discreta. Se obtiene contando el número de especies, por lo que solo puede tomar valores enteros (e.g., 15, 22, 30 especies).
  2. Acidez del agua (pH): Es una variable cuantitativa continua. El pH se mide en una escala y puede tomar cualquier valor dentro de un rango, como 8.1, 8.12, etc.
  3. Estado de blanqueamiento: Es una variable cualitativa ordinal. Las categorías ("Saludable", "Moderado", "Severo") tienen un orden claro que indica un empeoramiento de la salud del coral.

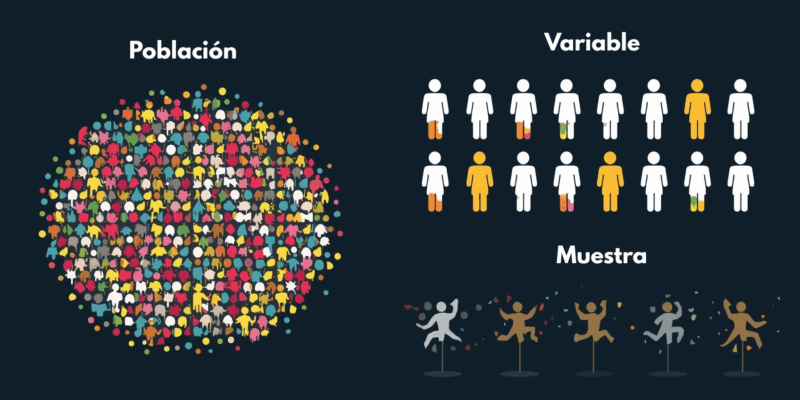
La Interconexión de los Conceptos: Un Resumen Visual 🧩

Población, muestra y variable no son conceptos aislados; son las piezas de un rompecabezas que encajan perfectamente para formar la base de cualquier análisis estadístico. El proceso mental es el siguiente:

1. ¿Qué quiero estudiar? -> Esto define tu POBLACIÓN.
2. ¿Puedo acceder a todos? Si la respuesta es no (que es lo más común) -> Debes seleccionar una MUESTRA representativa.
3. ¿Qué característica me interesa medir en mi muestra? -> Esa es tu VARIABLE.
4. ¿De qué tipo es mi variable? -> Esto determinará las herramientas estadísticas (gráficos, pruebas, modelos) que podrás usar para analizarla.

Imagina que la población es una olla gigante de sopa. Quieres saber si está bien de sal. Sería una locura (y un desperdicio) beberse toda la olla. En su lugar, tomas una muestra (una cucharada). La variable que te interesa es la "salinidad". Al probar la cucharada, infieres el sabor de toda la olla. Si tu cucharada no estaba bien mezclada (muestra no representativa), tu conclusión será incorrecta.

Ejercicios Resueltos Explicados Paso a Paso

Solución:

• • Población: Todas las personas en el mundo que padecen diabetes tipo 2. Esta es una población muy grande, considerada prácticamente infinita para fines del estudio.
  • Muestra: Los 500 voluntarios con diabetes tipo 2 que participan en el ensayo clínico.
  • Variables:
    1. Nivel de glucosa en ayunas: Es una variable cuantitativa continua, ya que se mide y puede tomar cualquier valor decimal dentro de un rango (por ejemplo, \(140.5\) mg/dL).
    2. Sexo del paciente: Es una variable cualitativa nominal. Las categorías (masculino, femenino) no tienen un orden jerárquico.
    3. Efectos secundarios reportados: Es una variable cualitativa ordinal. Las categorías ("ninguno", "leve", "severo") representan un orden creciente de intensidad del efecto.

Solución:

• • • Población: Todos los paneles solares del nuevo modelo instalados en esa región.
    • Muestra: El conjunto de paneles solares instalados en los 40 hogares seleccionados.
    • Variables:
      1. Producción diaria de energía: Variable cuantitativa continua. La energía (kWh) es una medida que puede tener valores decimales, como \(15.35\) kWh.
      2. Número de días nublados por semana: Variable cuantitativa discreta. Es el resultado de un conteo (\(0, 1, 2, ..., 7\)) y no puede tomar valores intermedios.
      3. Material del techo: Variable cualitativa nominal. Son categorías sin un orden específico (teja, metal, madera).

Solución:

• • • • Población: Los 2 millones de clientes del banco.
      • Muestra: Los 10,000 clientes que recibieron la encuesta (o, más precisamente, los que la respondieron).
      • Variables:
        1. Calificación de satisfacción (1 al 5): Variable cualitativa ordinal. Aunque se usan números, representan categorías ordenadas de satisfacción. La diferencia entre \(1\) y \(2\) no es necesariamente la misma que entre \(4\) y \(5\).
        2. Número de visitas a la sucursal: Variable cuantitativa discreta. Es un conteo de visitas (\(0, 1, 2, ...\)).
        3. Principal servicio utilizado: Variable cualitativa nominal. Son categorías que nombran servicios sin un orden inherente.

Solución:

• • • • • Población: Todos los vehículos que circulan por la autopista principal durante el período de estudio.
        • Muestra: Los vehículos que pasan por los 5 puntos donde están instalados los sensores.
        • Variables:
          1. Velocidad promedio de los vehículos: Variable cuantitativa continua. La velocidad es una medición que puede tomar cualquier valor en un rango, por ejemplo \(85.7\) km/h.
          2. Número de vehículos por hora: Variable cuantitativa discreta. Se obtiene contando los vehículos.
          3. Tipo de vehículo: Variable cualitativa nominal. Clasifica a los vehículos en categorías sin un orden jerárquico.

Ejercicios para razonar

Conclusión: Los Pilares de la Toma de Decisiones Basada en Datos 🚀

¡Felicidades! 🎉 Has dominado los tres conceptos más fundamentales de la estadística. Comprender la diferencia entre población y muestra es crucial para entender el alcance y las limitaciones de cualquier estudio. Saber identificar y clasificar las variables estadísticas es el primer paso para realizar un análisis correcto y significativo.

Estos conceptos son el lenguaje universal de la ciencia, la ingeniería, la economía, la medicina y muchas otras disciplinas. Son la base que nos permite pasar de la anécdota a la evidencia, de la intuición a la conclusión informada. La próxima vez que leas una noticia sobre una encuesta electoral, un estudio médico o un informe financiero, fíjate en cómo se definen estos tres elementos. Verás que están por todas partes, trabajando silenciosamente para dar forma a nuestro conocimiento del mundo.

Ahora tienes los cimientos. El siguiente paso es aprender a describir tus datos con la estadística descriptiva y a extraer conclusiones poderosas con la estadística inferencial. ¡El universo de los datos te espera!