Solución Problema 2 Ley de Cosenos

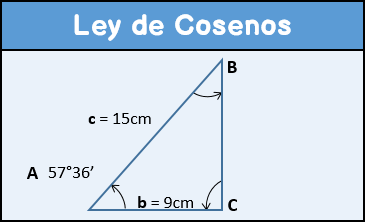
En el siguiente ejercicio 2 resuelto de la Ley de Cosenos, se vuelve a plantear el problema, el triángulo y su solución.

Nivel de Dificultad: 

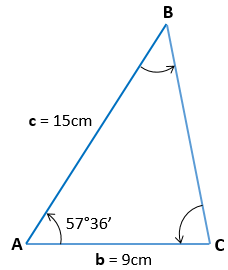
Solución:

Al igual que en el ejercicio anterior, necesitamos recabar los datos que nos proporciona el problema y empezar a resolver con la fórmula de la Ley de Cosenos.

b = 9 cm.

c = 15 cm.

<A = 57°36'

Antes de comenzar a resolver el ejercicio, es importante hacer una conversión de las unidades de minutos y pasarlas a grados, para ello vemos que el ángulo A, posee 57° con 36 minutos, entonces realizamos.

${\displaystyle \begin{array}{l}{60}^{\prime }\to 1{}^{\circ }\\ {36}^{\prime }\to x{}^{\circ }\end{array}}$

Aplicamos nuestro despeje:

${\displaystyle x{}^{\circ }=\frac{\left({36}^{\prime }\right)\left(1{}^{\circ }\right)}{{60}^{\prime }}=0.6{}^{\circ }}$

Por lo que realmente el ángulo A, tiene:

${\displaystyle \sphericalangle A=57.6{}^{\circ }}$

Teniendo este dato, ya podemos realizar el cálculo correspondiente para completar los datos del triángulo oblicuángulo. A simple vista nos hace falta el lado a, por lo que aplicamos la fórmula para obtenerlo:

Obteniendo el lado a

${\displaystyle a^2=b^2+c^2-2bc\cos A}$

${\displaystyle a=\sqrt{b^2+c^2-2bc\cos A}}$

Sustituyendo los datos en la fórmula tenemos:

${\displaystyle a=\sqrt{{(9cm)}^2+{(15cm)}^2-2(9cm)(15cm)cos(57.6{}^{\circ })}}$

${\displaystyle a=\sqrt{306c{m}^2-144.6732c{m}^2}}$

${\displaystyle a=\sqrt{161.3267c{m}^2}}$

${\displaystyle a=12.7cm}$

∴ a = 12.7 cm.

Obteniendo el ángulo B

Usaremos nuestra fórmula

${\displaystyle \cos B=\frac{a^2+c^2-b^2}{2ac}}$

sustituyendo nuestros datos, tendremos:

${\displaystyle \cos B=\frac{{(12.7cm)}^2+{(15cm)}^2-{(9cm)}^2}{2(12.7cm)(15cm)}=\frac{305.29c{m}^2}{381c{m}^2}=0.8012}$

Despejando B

${\displaystyle B=\arccos (0.8012)=36.76{}^{\circ }}$

Obteniendo el ángulo C

${\displaystyle \cos C=\frac{{(12.7cm)}^2+{(9cm)}^2-{(15cm)}^2}{2(12.7cm)(9cm)}=\frac{17.29c{m}^2}{228.6c{m}^2}=0.0756}$

Despejando C

${\displaystyle C=\arccos (0.0756)=85.66{}^{\circ }}$

Resultados

${\displaystyle \begin{array}{l}\sphericalangle A={57.6}^{{}^{\circ }}\\ \sphericalangle B={36.75}^{{}^{\circ }}\\ \sphericalangle C={85.66}^{{}^{\circ }}\end{array}}$

Es posible que en algunos casos al sumar los ángulos internos, las centésimas se pasen por 1 o 2, esto es porque al momento de ir elevando al cuadrado cada factor, hemos ido ya sea truncando o redondeando los valores.