Distancia entre Dos Puntos - Ejercicios Resueltos

Dentro de la Geometría Analítica existen varios temas de gran interés, pero para poder comprender la mayoría de ellos es de vital importancia conocer las bases o principios que fundamentan esta área. Una de ellas es la distancia entre dos puntos.

Vamos analizar los tres casos de estudio más importantes para poder simplificar los cálculos, y con ello darnos cuenta de identificar la formula y resolver ejercicios sin caer en el error. 🤓

Fórmula de la distancia entre dos Puntos

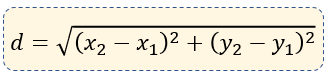
Antes de comenzar analizar los casos, es recomendable decir; que los tres casos hacen referencia a la solución del mismo problema, solamente que se analizan de una forma que se pueda entender mejor el tema de la distancia dirigida y no dirigida. Y con ello poder llegar a la fórmula de la distancia entre dos puntos general.

🔸 Distancia Horizontal Entre Dos puntos

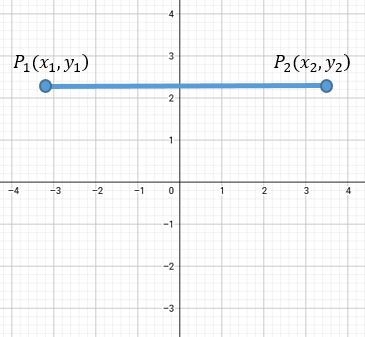
Imaginemos que tenemos dos pares ordenados P1(x1, y1) y P2(x2, y2), tales puntos están localizados de tal forma que éstas formen una recta horizontal, es decir, paralela al eje de las abscisas o eje "x". Para poder calcular la distancia entre tales puntos es:

$\displaystyle {{p}_{1}}{{p}_{2}}={{x}_{2}}-{{x}_{1}}$

Recordemos que si la recta va del punto 1 hasta el punto 2, entonces tomamos la parte final menos la parte inicial. De otra forma:

$\displaystyle {{p}_{2}}{{p}_{1}}={{x}_{1}}-{{x}_{2}}$

En este caso vamos del punto 2 hasta el punto 1, por lo que nuestro punto inicial es x1 y el final x2.

En cualquier caso que deseemos tomar como punto inicial o final, la distancia siempre será la misma, a ese procedimiento de cantidad absoluta, se le conoce como distancia no dirigida.

Nuestra Fórmula para la distancia horizontal entre dos puntos, es la siguiente:

$\displaystyle \left| {{P}_{1}}{{P}_{2}} \right|=\left| {{x}_{2}}-{{x}_{1}} \right|=\left| {{x}_{1}}-{{x}_{2}} \right|$

🔸 Distancia Vertical Entre Dos puntos

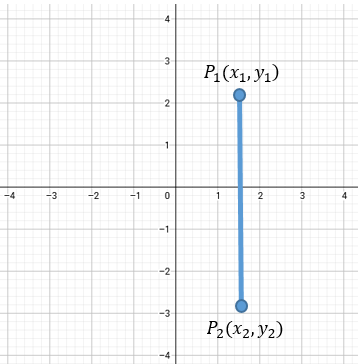
Al igual que la distancia entre dos puntos horizontal, en la distancia vertical podemos tomar dos puntos cualesquiera que pertenezcan a una misma recta de forma vertical, es decir que sea paralela al eje de las ordenadas, o eje "y". Para poder calcular la distancia realizamos el siguiente argumento:

Sea la distancia dirigida del punto 1 al punto 2.

$\displaystyle {{P}_{1}}{{P}_{2}}={{y}_{2}}-{{y}_{1}}$

Ahora, si deseamos encontrar la distancia del punto 2 al punto 1.

$\displaystyle {{P}_{2}}{{P}_{1}}={{y}_{1}}-{{y}_{2}}$

Y si lo que realmente deseamos es calcular la distancia desde cualquier punto, como una distancia no dirigida, entonces aplicamos lo que sería nuestra fórmula.

$\displaystyle \left| {{P}_{1}}{{P}_{2}} \right|=\left| {{y}_{2}}-{{y}_{1}} \right|=\left| {{y}_{1}}-{{y}_{2}} \right|$

🔸 Distancia Entre Dos Puntos General

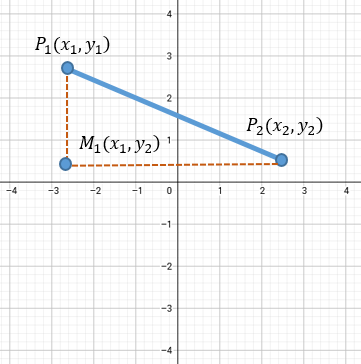
En este tercer caso la situación se vuelve más interesante, porque veremos aplicar una técnica que debimos aprender en Geometría y Trigonometría.

Pues bien, al observar la imagen de la distancia entre dos puntos, nos damos cuenta que los puntos ya no se encuentran de forma horizontal, ni de forma vertical. Si no que ahora están en forma de diagonal, pero para buen observador también nos percatamos que hay un punto M (x1, y2), donde su par ordenado tiene la abscisa del punto 1, y tiene la ordenada del punto 2. Esto finalmente forma un triángulo rectángulo.

Dónde:

$\displaystyle \left| {{P}_{1}}{{P}_{2}} \right|=hipotenusa$

$\displaystyle {{M}_{1}}{{P}_{2}}={{x}_{2}}-{{x}_{1}}$ Cateto Adyacente

$\displaystyle {{P}_{1}}{{M}_{1}}={{y}_{2}}-{{y}_{1}}$ Cateto Opuesto

Como podemos ver, para poder calcular la distancia entre el punto 1 y el punto 2, es necesario recurrir al Teorema de Pitágoras

Aplicando el Teorema de Pitágoras, tenemos:

$\displaystyle {{\left( {{P}_{1}}{{P}_{2}} \right)}^{2}}={{\left( {{M}_{1}}{{P}_{2}} \right)}^{2}}+{{\left( {{P}_{1}}{{M}_{1}} \right)}^{2}}$

Para quitar el cuadrado del primer miembro, obtenemos la raíz cuadrada de ambos miembros, quedando así.

$\displaystyle \sqrt{{{\left( {{P}_{1}}{{P}_{2}} \right)}^{2}}}=\sqrt{{{\left( {{M}_{1}}{{P}_{2}} \right)}^{2}}+{{\left( {{P}_{1}}{{M}_{1}} \right)}^{2}}}$

$\displaystyle {{P}_{1}}{{P}_{2}}=\sqrt{{{\left( {{M}_{1}}{{P}_{2}} \right)}^{2}}+{{\left( {{P}_{1}}{{M}_{1}} \right)}^{2}}}$

Sustituyendo por los pares ordenados, esto queda así:

$\displaystyle {{P}_{1}}{{P}_{2}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

Qué finalmente la podemos escribir de esta forma.

$\displaystyle d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

La forma general de calcular la distancia entre dos puntos, estén donde estén. La fórmula aplica siempre. 😎

Ejemplos Resueltos de Distancia entre Dos Puntos

Solución: Observando las coordenadas, podemos darnos cuenta que sobre el eje "y" no se mueve para nada, por lo que se trata de una recta totalmente horizontal.

Si deseamos calcular la distancia, simplemente aplicamos nuestra fórmula:

$\displaystyle {{P}_{1}}{{P}_{2}}={{x}_{2}}-{{x}_{1}}=4-(-5)=4+5=9$

Por lo que hay una distancia de 9 unidades.

Solución:

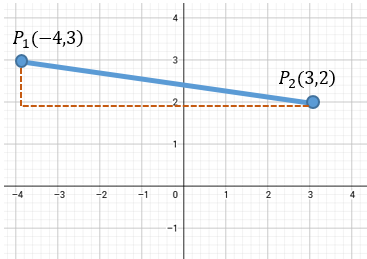
En este ejemplo es diferente, vemos que hay una distancia que tenemos que calcular aplicando la fórmula de la distancia entre dos puntos general.

Elegimos cualquier punto, puede ser el Punto 1, o puede ser el Punto 2. No importa a quién tomemos como inicial, el resultado debe ser el mismo. En este caso vamos elegir al punto uno como inicial, y punto dos como final.

De nuestra fórmula:

$\displaystyle d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

$\displaystyle d=\sqrt{{{\left( 3-(-4) \right)}^{2}}+{{\left( 2-3 \right)}^{2}}}$

$\displaystyle d=\sqrt{{{(3+4)}^{2}}+{{(-1)}^{2}}}$

$\displaystyle d=\sqrt{{{(7)}^{2}}+{{(1)}^{2}}}=\sqrt{49+1}=\sqrt{50}$

$\displaystyle d\approx 7.071$

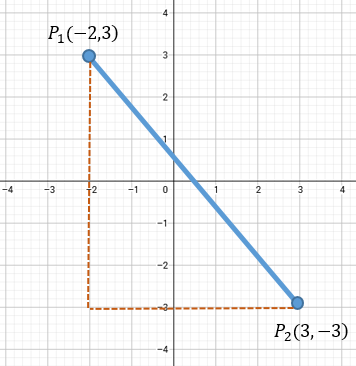
Solución: 

Al igual que el ejercicio anterior, para poder calcular la distancia entre los dos puntos (P1P2), es necesario aplicar la fórmula que implica el teorema de pitágoras.

Vamos a tomar para este ejemplo P1P2 (P1 como punto inicial y P2 como punto final).

Quedando así:

$\displaystyle d=\sqrt{{{\left( 3-(-2) \right)}^{2}}+{{\left( -3-3 \right)}^{2}}}$

$\displaystyle d=\sqrt{{{\left( 3+2 \right)}^{2}}+{{\left( -6 \right)}^{2}}}$

$\displaystyle d=\sqrt{{{(5)}^{2}}+36}$

$\displaystyle d=\sqrt{61}$

$\displaystyle d\approx 7.810$

Intentemos subir un poco el nivel, y veamos otro ejemplo donde usemos un poco más el recurso del álgebra.

Solución:

No podemos bosquejar la recta, porque nos hace falta la abscisa, y es justo lo que el problema nos pide, sin embargo podemos puntualizar nuestros datos, para ver el procedimiento que llevaremos a cabo, entonces.

d = 17

Punto A = (1, -11)

Punto B = (x2, 4)

Llamaremos a "x2" a la abscisa que no conocemos, y que vamos a encontrar. Si establecemos la fórmula de la distancia entre dos puntos, tendríamos lo siguiente:

$\displaystyle d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

Vamos a despejar a "x2" de la fórmula. Si tienes problemas de despeje, puedes ir a nuestro artículo de Aprende a como despejar fórmulas

Entonces, quitamos la raíz cuadrada elevando ambos miembros al cuadrado

$\displaystyle {{d}^{2}}={{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}$

Con esto eliminamos la raíz cuadrada del segundo miembro, ahora pasemos la cantidad que está sumando de "y2-y1" al primer miembro y ésta pasará a restar.

$\displaystyle {{d}^{2}}-{{({{y}_{2}}-{{y}_{1}})}^{2}}={{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}$

Donde está nuestra incógnita "x2" todavía tenemos un binomio al cuadrado, así que procedemos a sacar la raíz en ambos miembros.

$\displaystyle \sqrt{{{d}^{2}}-{{({{y}_{2}}-{{y}_{1}})}^{2}}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}}$

$\displaystyle \sqrt{{{d}^{2}}-{{({{y}_{2}}-{{y}_{1}})}^{2}}}={{x}_{2}}-{{x}_{1}}$

Perfecto, ahora solo despejamos a nuestra incógnita, pasando a sumar a "x1" al primer miembro.

$\displaystyle \sqrt{{{d}^{2}}-{{({{y}_{2}}-{{y}_{1}})}^{2}}}+{{x}_{1}}={{x}_{2}}$

Invertimos la igualdad, y tenemos finalmente lo que deseamos.

$\displaystyle {{x}_{2}}=\sqrt{{{d}^{2}}-{{({{y}_{2}}-{{y}_{1}})}^{2}}}+{{x}_{1}}$

Ahora simplemente sustituimos nuestros datos en lo que hemos despejado de la fórmula, y veremos el resultado.

$\displaystyle {{x}_{2}}=\sqrt{{{17}^{2}}-{{(4-(-11))}^{2}}}+1$

$\displaystyle {{x}_{2}}=\sqrt{{{17}^{2}}-{{(4+11)}^{2}}}+1=\sqrt{289-{{(15)}^{2}}}+1$

Y luego

$\displaystyle {{x}_{2}}=\pm \sqrt{64}+1$

Al extraer la raíz cuadrada de 64, recordemos que debemos tomar un valor + (positivo) y un - (negativo).

$\displaystyle {{x}_{2}}=\pm 8+1$

Por lo que tendríamos dos abscisas, una sería:

$\displaystyle {{x}_{21}}=9$

Y la otra

$\displaystyle {{x}_{22}}=-7$

Esto nos llevaría a tener 3 puntos en el plano cartesiano.

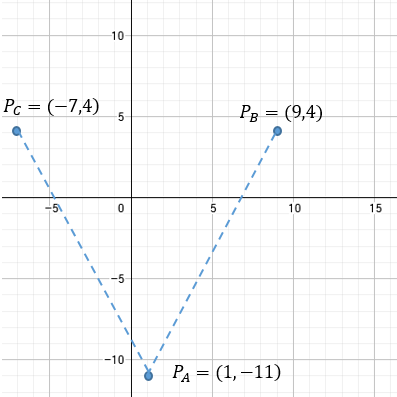
$\displaystyle \begin{array}{l}{{P}_{A}}=(1,-11)\\{{P}_{B}}=(9,4)\\{{P}_{C}}=(-7,4)\end{array}$

Sin duda éste problema es un problema más completo para comprender la importancia de las abscisas y ordenadas en un punto, y las formas en como podemos encontrarnos algunos problemas.