División de un Segmento En Una Razón Dada - Ejemplos

Durante nuestro estudio de la Geometría Analítica, nos vamos a encontrar con un método interesante para poder calcular las coordenadas de un punto P (o sea un punto cualquiera que llamamos "P"), que está dividido por un segmento cuyas extremidades son el P1 (x1, y1) y P2 (x2, y2) en la razón dada por la siguiente relación:

$\displaystyle r=\frac{{{P}_{1}}P}{P{{P}_{2}}}$

Hasta este punto puede ser confuso lo explicado, pero no es necesario enredarse con la definición. Mas abajo veremos la definición en una gráfica y nos daremos una mejor idea de lo que intentamos explicar, y ver como llevar a cabo el procedimiento para encontrar la fórmula de la división de un segmento en una razón dada , y poder resolver ejercicios sin dificultad alguna. Es necesario que para estudiar este tema se tenga idea de como despejar variables y conocimiento de álgebra.

Obtención de la Fórmula de la División de un Segmento dada una Razón

Bien, analicemos entonces la siguiente gráfica.

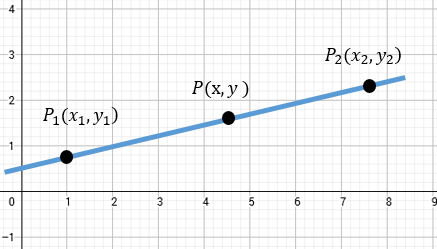
Si sabemos que la razón está dada mediante la relación:

$\displaystyle r=\frac{{{P}_{1}}P}{P{{P}_{2}}}$

Vamos a proyectar las coordenadas de los puntos en los dos ejes. De la siguiente manera.

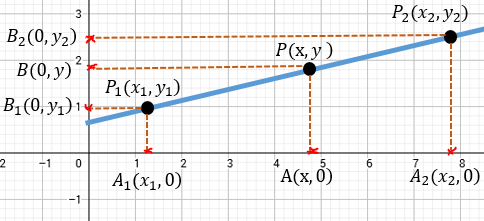
Bien, ahora tenemos las proyecciones en el eje de las abscisas "x", con los puntos A, y sobre el eje de las ordenadas "y" para los puntos B. Estos nos servirán de referencia para poder obtener nuestra fórmula, entonces vamos a relacionar lo siguiente:

$\displaystyle \frac{{{P}_{1}}P}{P{{P}_{2}}}=\frac{{{A}_{1}}A}{A{{A}_{2}}}$

Ahora veamos las distancias dirigidas, ¿no recuerdas qué son?, puedes regresar al tema de Distancia entre Dos Puntos , si ya recuerdas que son, entonces es momento de aplicar dicho conocimiento, para relacionar lo siguiente:

$\displaystyle {{A}_{1}}A=x-{{x}_{1}}$

y hacemos lo mismo con el siguiente segmento de AA2

$\displaystyle A{{A}_{2}}={{x}_{2}}-x$

Perfecto, ahora podemos sustituir estos datos en la fórmula de la razón.

$\displaystyle r=\frac{{{P}_{1}}P}{P{{P}_{2}}}=\frac{{{A}_{1}}A}{A{{A}_{2}}}=\frac{x-{{x}_{1}}}{{{x}_{2}}-x}$

Como "x" es la que estamos buscando, porque forma parte del punto del segmento, entonces procedemos a despejar. Si no recuerdas como despejar, recuerda Aprende a como despejar fórmulas

$\displaystyle r=\frac{x-{{x}_{1}}}{{{x}_{2}}-x}$

Procedemos a despejar:

$\displaystyle r({{x}_{2}}-x)=x-{{x}_{1}}$

Operamos lo del primer miembro

$\displaystyle r{{x}_{2}}-rx=x-{{x}_{1}}$

Acomodamos a las "x" en el primer miembro, quedando así:

$\displaystyle -rx-x=-{{x}_{1}}-r{{x}_{2}}$

Multiplicamos todo por (-1), para que se vuelvan positivos.

$\displaystyle rx+x={{x}_{1}}+r{{x}_{2}}$

Factorizamos a "x" en el primer miembro.

$\displaystyle x(r+1)={{x}_{1}}+r{{x}_{2}}$

Despejamos el monomio que está multiplicando a "x", quedando así nada más la variable que necesitamos.

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}$

Quedando así nuestra "x" despejada totalmente, ¡Solo que aplicaremos una condición!.

$\displaystyle r\ne -1$

nuestra razón no puede ser igual a (-1) porque esto nos haría indeterminado nuestra operación, y no está definida.

• Para obtener "y", hacemos exactamente el mismo cálculo y procedimiento.

$\displaystyle r=\frac{{{P}_{1}}P}{P{{P}_{2}}}=\frac{{{B}_{1}}B}{B{{B}_{2}}}=\frac{y-{{y}_{1}}}{{{y}_{2}}-y}$

$\displaystyle r=\frac{y-{{y}_{1}}}{{{y}_{2}}-y}$

$\displaystyle r({{y}_{2}}-y)=y-{{y}_{1}}$

$\displaystyle r{{y}_{2}}-ry=y-{{y}_{1}}$

$\displaystyle -ry-y=-{{y}_{1}}-r{{y}_{2}}$

$\displaystyle ry+y={{y}_{1}}+r{{y}_{2}}$

$\displaystyle y(r+1)={{y}_{1}}+r{{y}_{2}}$

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}$

La misma condición respecto a el valor que no puede obtener "r"

$\displaystyle r\ne -1$

Fórmula de la División de un Segmento en una Razón Dada

Cómo vimos anteriormente, ya hemos encontrado la fórmula que aplicaremos de aquí en adelante para resolver ejercicios de este tema, y con ello podrás resolver hasta más de 10 ejemplos.

Para encontrar las coordenadas de punto P que divide al segmento, es la siguiente:

Fórmula:

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}$

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}$

Con la siguiente condición:

$\displaystyle r\ne -1$

Ahora, también podemos encontrar la fórmula del punto medio de un segmento, suponiendo que la distancia entre el segmento P1P sea igual a la distancia con PP2. Por lo que la razón sería igual a la unidad.

$\displaystyle r=\frac{{{P}_{1}}P}{P{{P}_{2}}}=1$

Sustituyendo en la fórmula:

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}=\frac{{{x}_{1}}+(1){{x}_{2}}}{1+1}=\frac{{{x}_{1}}+{{x}_{2}}}{2}$

Ahora para "y"

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}=\frac{{{x}_{1}}+(1){{y}_{2}}}{1+1}=\frac{{{y}_{1}}+{{y}_{2}}}{2}$

Fórmula del Punto Medio

$\displaystyle x=\frac{{{x}_{1}}+{{x}_{2}}}{2}$

$\displaystyle y=\frac{{{y}_{1}}+{{y}_{2}}}{2}$

📄 Ejercicios Resueltos Paso a Paso

Comencemos con los siguientes ejercicios resueltos paso a paso, y verás que no es difícil.

Solución: 

Sin tanta complicación, podemos utilizar nuestras fórmulas y sustituir nuestros datos.

Recordar que en el punto A, tenemos lo siguiente:

$\displaystyle {{x}_{1}}=5$

$\displaystyle {{y}_{1}}=3$

Y para el punto B

$\displaystyle {{x}_{2}}=-2$

$\displaystyle {{y}_{2}}=8$

Ahora, sustituyendo tenemos:

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}=\frac{5+\left( \frac{3}{4} \right)\left( -2 \right)}{\frac{3}{4}+1}=\frac{5-\frac{6}{4}}{\frac{7}{4}}=\frac{\frac{14}{4}}{\frac{7}{4}}=\frac{14(4)}{7(4)}=\frac{14}{7}=2$

$\displaystyle x=2$

Concluimos que x = 2, ahora hagamos lo mismo para "y".

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}=\frac{3+\left( \frac{3}{4} \right)(8)}{\frac{3}{4}+1}=\frac{3+\frac{24}{4}}{\frac{7}{4}}=\frac{3+6}{\frac{7}{4}}=\frac{9}{\frac{7}{4}}=\frac{36}{7}\approx 5.143$

$\displaystyle y\approx 5.143$

El valor de "y" será un valor aproximadamente de 5.143.

De forma gráfica esto es.

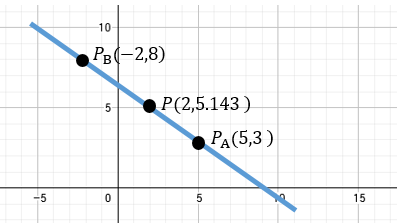
Veamos otro ejemplo 😎

Solución:

Aunque parezca un problema diferente al anterior, sigue siendo muy similar. La idea de que encontremos las coordenadas del centro de una circunferencia sin antes haber visto el tema de las diversas figuras en el plano cartesiano no debe causar confusión. Si ya tenemos las coordenadas de el diámetro, entonces por intuición debemos saber que la razón será la unidad, puesto que a la mitad del diámetro, lo que realmente tenemos es el punto medio así que tracemos nuestras coordenadas en el plano cartesiano.

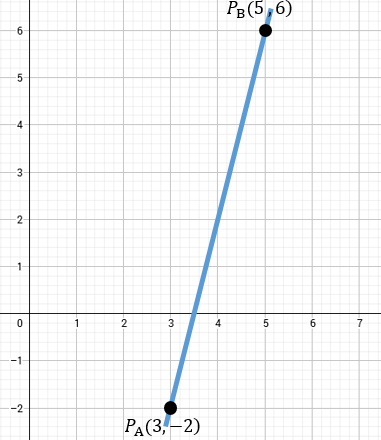
Al momento de realizar nuestro cálculo, considerando a r = 1

$\displaystyle {{P}_{A}}=(3,-2)$

$\displaystyle {{P}_{B}}=(5,6)$

Ahora sustituimos.

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}=\frac{3+\left( 1 \right)\left( 5 \right)}{1+1}=\frac{3+5}{2}=\frac{8}{2}=4$

Bien, ahora hagamos lo mismo pero para "y"

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}=\frac{-2+\left( 1 \right)\left( 6 \right)}{1+1}=\frac{-2+6}{2}=\frac{4}{2}=2$

Por lo tanto las coordenadas buscadas para el Centro es C (4,2). Quedando así:

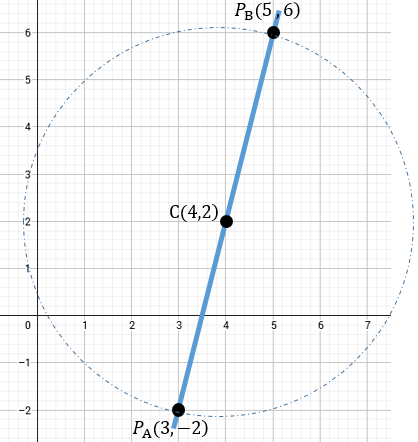
Genial! Ahora veamos otro ejemplo.

Solución:

Al igual que en el ejercicio 1, debemos asignar las coordenadas de los dos puntos. De tal forma que:

Punto A

$\displaystyle {{x}_{1}}=-2$

$\displaystyle {{y}_{1}}=5$

Punto B

$\displaystyle {{x}_{2}}=10$

$\displaystyle {{y}_{2}}=-2$

Ahora sustituimos en la fórmula para encontrar la abscisa del punto P

$\displaystyle x=\frac{{{x}_{1}}+r{{x}_{2}}}{r+1}=\frac{-2+\left( \frac{2}{3} \right)\left( 10 \right)}{\frac{2}{3}+1}=\frac{-2+\frac{20}{3}}{\frac{5}{3}}=\frac{\frac{14}{3}}{\frac{5}{3}}=\frac{14(3)}{5(3)}$

$\displaystyle x=\frac{14}{5}=2.8$

Ahora pasamos a calcular a la ordenada del punto P

$\displaystyle y=\frac{{{y}_{1}}+r{{y}_{2}}}{r+1}=\frac{5+\left( \frac{2}{3} \right)\left( -2 \right)}{\frac{2}{3}+1}=\frac{5-\frac{4}{3}}{\frac{5}{3}}=\frac{\frac{11}{3}}{\frac{5}{3}}=\frac{11(3)}{5(3)}$

$\displaystyle y=\frac{11}{5}=2.2$

Quedando así finalmente nuestro problema.

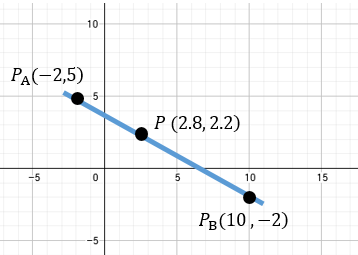
Con esto tenemos prácticamente el ejercicio completado. Esperamos haya sido totalmente de tu agrado y comprensión. Si hay dudas, escribirlas abajo en la caja de comentarios 😎