Segunda Condición de Equilibrio - Ejercicios Resueltos + [PDF]

Si alguna vez has jugado en un subibaja, has usado una llave de tuercas para cambiar una llanta o simplemente has abierto una puerta, has aplicado la Segunda Condición de Equilibrio sin saberlo. En física, esto se conoce comúnmente como Torque o Momento de Fuerza, y es la razón por la que las cosas giran... o se mantienen estables sin girar.

Es probable que algunos libros o profesores la llamen erróneamente "Segunda Ley de Equilibrio", pero el término correcto es condición. Hoy vamos a dominar este tema con teoría clara y ejercicios prácticos.

¿Qué es la Segunda Condición de Equilibrio?

Para entender esto, recordemos la Primera Condición de Equilibrio: nos dice que si la suma de fuerzas es cero, el cuerpo no se traslada (no se mueve de un lado a otro).

Pero, ¿qué pasa con los giros? Un cuerpo puede tener fuerza neta cero y aun así estar girando como loco (piensa en un volante). Para que un cuerpo esté totalmente quieto (Equilibrio Estático Total), no debe ni trasladarse ni rotar.

Matemáticamente se escribe así:

¿Qué es el Torque o Momento? (\(M\))

Es la capacidad de una fuerza para producir un giro. No basta con aplicar fuerza; importa dónde la aplicas. La fórmula básica es:

\[ \tau = F \cdot d \]

Donde:

• \(\tau\) o \(M\): Torque o Momento [N·m] (Newton-metro).
• \(F\): Fuerza aplicada [N].
• \(d\): Brazo de palanca (distancia perpendicular desde el eje de giro a la fuerza) [m].

Regla de los Signos (¡Vital para Aprobar!)

Aquí es donde la mayoría falla. Debemos definir cuándo un giro es positivo o negativo. Por convención general en física e ingeniería usamos:

La siguiente imagen de nuestro archivo lo ilustra perfectamente:

Concepto: Par de Fuerzas

A veces verás ejercicios donde hay dos fuerzas iguales en magnitud y dirección, pero sentidos contrarios, aplicadas en puntos distintos. A esto se le llama Par de Fuerzas.

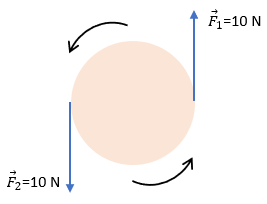
En la imagen anterior, la fuerza \(F_1\) intenta girar el disco en sentido antihorario (+) y la \(F_2\) también ayuda al giro antihorario (si tomamos el centro como pivote). ¡El disco girará!

Análisis de Casos: Entendiendo el Brazo de Palanca

Antes de pasar a los problemas complejos, analicemos estos 4 casos básicos que suelen confundir. Analízalos bien, porque son la base de todo.

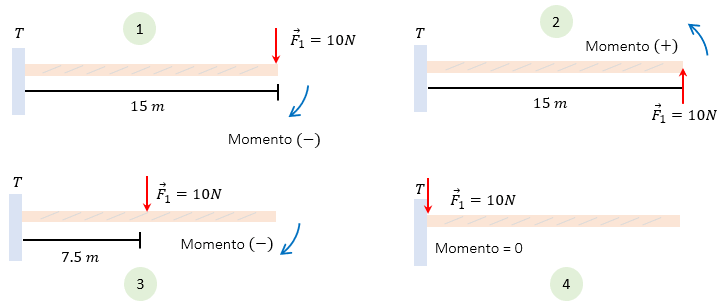
Análisis Rápido:

• Caso 1: Fuerza hacia abajo a 15m. Giro Horario \(\to\) Torque Negativo.
• Caso 2: Fuerza hacia arriba a 15m. Giro Antihorario \(\to\) Torque Positivo.
• Caso 3: Misma fuerza, pero a mitad de distancia (7.5m). El Torque será la mitad que en el caso 1.
• Caso 4 (El más importante): La fuerza se aplica JUSTO en el punto de apoyo. La distancia \(d=0\). Por lo tanto, Torque = 0. (¡Recuerda esto! Las fuerzas en el pivote se anulan).

✅ Ejercicios Resueltos de Segunda Condición de Equilibrio

Ahora sí, vamos a resolver problemas tipo examen. El secreto es: Elegir un buen punto de pivote y hacer la sumatoria de momentos.

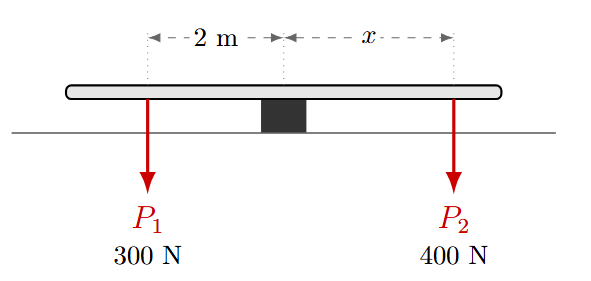
Solución:
Primero convertimos las masas a Peso (Fuerza):
\(P_1 = 30 \text{ kg} \times 10 = 300 \text{ N}\) (Niño izquierda)
\(P_2 = 40 \text{ kg} \times 10 = 400 \text{ N}\) (Niño derecha)

Aplicamos la Segunda Condición de Equilibrio (\(\sum \tau = 0\)) respecto al centro (pivote):
1. El niño de la izquierda hace girar antihorario (+).
2. El niño de la derecha hace girar horario (-).

\[ \tau_1 - \tau_2 = 0 \]
\[ (P_1 \cdot d_1) - (P_2 \cdot d_2) = 0 \]

Sustituimos los datos conocidos (\(d_1 = 2 \text{ m}\), \(d_2 = x\)):
\[ (300 \text{ N})(2 \text{ m}) - (400 \text{ N})(x) = 0 \]
\[ 600 - 400x = 0 \]
\[ 600 = 400x \]
Despejamos \(x\):
\[ x = \frac{600}{400} = 1.5 \text{ m} \]

Resultado: El segundo niño debe sentarse a 1.5 metros del centro.

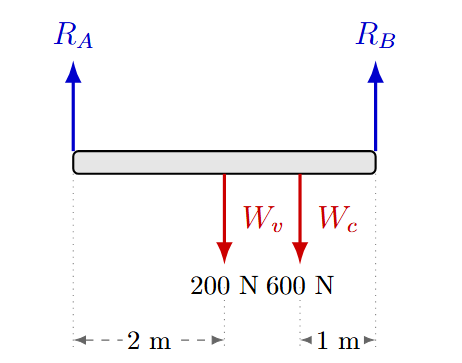
[Image of beam supported at ends with load]

Solución:
Este problema combina la Primera y Segunda condición.
Fuerzas involucradas:
\(R_A\): Reacción en A (Arriba).
\(R_B\): Reacción en B (Arriba).
\(W_{\text{viga}} = 200 \text{ N}\): Actúa en el centro geométrico (a 2m de A).
\(W_{\text{caja}} = 600 \text{ N}\): Está a 1m de B (o sea, a 3m de A).

Paso 1: Sumatoria de Torques en el punto A (\(\sum \tau_A = 0\))
Elegimos A como pivote para eliminar \(R_A\) de la ecuación (su distancia es 0).
Peso Viga (200 N) \(\to\) Giro Horario (-)
Peso Caja (600 N) \(\to\) Giro Horario (-)
Reacción B (\(R_B\)) \(\to\) Giro Antihorario (+)

\[ -(200 \text{ N})(2 \text{ m}) - (600 \text{ N})(3 \text{ m}) + R_B(4 \text{ m}) = 0 \]
\[ -400 - 1800 + 4R_B = 0 \]
\[ -2200 + 4R_B = 0 \]
\[ 4R_B = 2200 \Rightarrow R_B = \frac{2200}{4} = 550 \text{ N} \]

Paso 2: Sumatoria de Fuerzas Verticales (\(\sum F_y = 0\))
Como la viga no sube ni baja:
\[ R_A + R_B - 200 - 600 = 0 \]
\[ R_A + 550 - 800 = 0 \]
\[ R_A - 250 = 0 \Rightarrow R_A = 250 \text{ N} \]

Resultado: La reacción en A es 250 N y en B es 550 N.

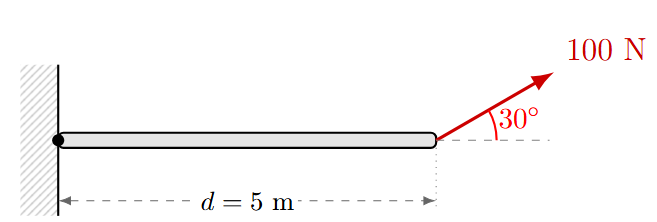
Solución:
Cuando la fuerza no es perpendicular al brazo de palanca, usamos la componente perpendicular (\(F \sin \theta\)).
La fórmula general es:
\[ \tau = F \cdot d \cdot \sin(\theta) \]

Datos:
\(F = 100 \text{ N}\)
\(d = 5 \text{ m}\)
\(\theta = 30^{\circ}\)

\[ \tau = 100 \cdot 5 \cdot \sin(30^{\circ}) \]
Recordando que \(\sin(30^{\circ}) = 0.5\):
\[ \tau = 500 \cdot 0.5 = 250 \text{ N}\cdot\text{m} \]

Resultado: El torque es de 250 N·m.

🚀 Ejercicios Avanzados (Escaleras y Tensiones)

Si ya dominaste los anteriores, es hora de subir de nivel. Estos son los problemas típicos que salen en los exámenes finales.

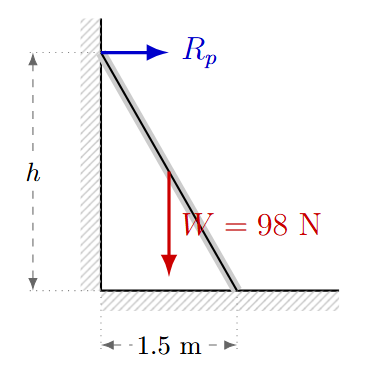
Solución:
Este problema requiere un buen diagrama.

1. Pivote: Elegimos el pie de la escalera (Punto A) para eliminar las reacciones del suelo (fricción y normal) que no conocemos.
2. Fuerzas que hacen torque respecto a A:
   • El Peso de la escalera (\(W = 10 \cdot 9.8 = 98 \text{ N}\)) actúa en el centro (a 2m de longitud).
   • La Reacción de la Pared (\(R_p\)) actúa en el extremo superior (a 4m de longitud), horizontalmente hacia la izquierda.

Cálculo de Ángulos y Brazos:
Necesitamos la altura de la pared (\(h\)) por Pitágoras:
\[ h = \sqrt{4^2 - 1.5^2} = \sqrt{16 - 2.25} = \sqrt{13.75} \approx 3.7 \text{ m} \]

Sumatoria de Torques (\(\sum \tau_A = 0\)):

• Torque del Peso (Giro Horario): El brazo de palanca es la distancia horizontal al centro. Si la base total es 1.5m, el centro está a 0.75m.
  \(\tau_W = -(98 \text{ N})(0.75 \text{ m})\)
• Torque de la Pared (Giro Antihorario): El brazo de palanca es la altura vertical (\(h\)).
  \(\tau_P = +(R_p)(3.7 \text{ m})\)

\[ -73.5 + 3.7 R_p = 0 \]
\[ 3.7 R_p = 73.5 \Rightarrow R_p = \frac{73.5}{3.7} \]

Resultado: La fuerza de la pared es 19.86 N.

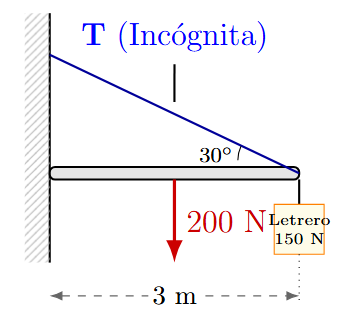
Solución:
Pivote en la bisagra (izquierda).
Fuerzas que generan torque:

1. Peso Barra (200 N) a 1.5 m (centro).
2. Peso Letrero (150 N) a 3 m (extremo).
3. Componente vertical de la Tensión (\(T \sin 30^\circ\)) a 3 m.

\[ \sum \tau = 0 \]
\[ -(200)(1.5) - (150)(3) + (T \sin 30^\circ)(3) = 0 \]
\[ -300 - 450 + T(0.5)(3) = 0 \]
\[ -750 + 1.5T = 0 \]
\[ 1.5T = 750 \Rightarrow T = \frac{750}{1.5} \]

Resultado: La tensión es 500 N.

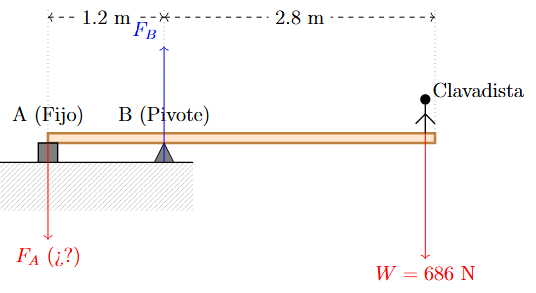
Solución:
Ojo aquí: Para mantener el equilibrio, el soporte A debe jalar hacia abajo (para contrarrestar el giro que hace el clavadista sobre el punto B).
Tomamos pivote en B (el soporte central) para hallar A.

• Peso Clavadista (\(W = 70 \cdot 9.8 = 686 \text{ N}\)). Distancia desde B = \(4 - 1.2 = 2.8 \text{ m}\). Giro Horario (-).
• Fuerza en A (\(F_A\)). Distancia desde B = 1.2 m. Para equilibrar, \(F_A\) debe generar torque Antihorario (+) (fuerza hacia abajo).

\[ \sum \tau_B = 0 \]
\[ -(686)(2.8) + F_A(1.2) = 0 \]
\[ -1920.8 + 1.2 F_A = 0 \]
\[ F_A = \frac{1920.8}{1.2} \]

Resultado: La fuerza en A es 1600.6 N (hacia abajo).

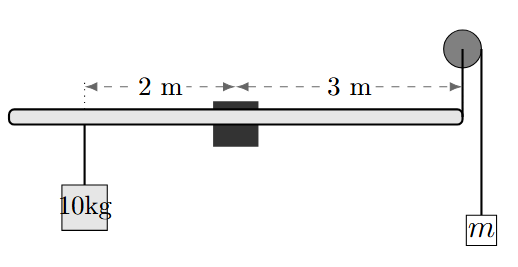
Solución:
Pivote en el centro.

• Torque Izquierda: \(W_1 = 10 \cdot 9.8 = 98 \text{ N}\) a 2m. Giro Antihorario (+).
• Torque Derecha: \(W_2 = m \cdot 9.8\) a 3m. Giro Horario (-).

\[ \sum \tau = 0 \]
\[ +(98)(2) - (m \cdot 9.8)(3) = 0 \]
\[ 196 - 29.4m = 0 \]
\[ m = \frac{196}{29.4} \]

Resultado: La masa debe ser 6.66 kg.

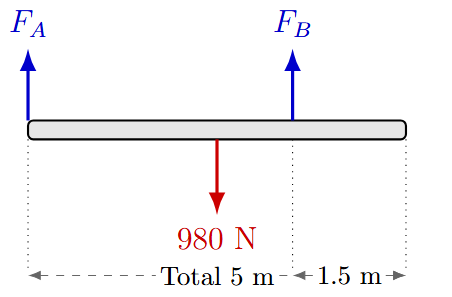
Solución:
Peso Viga = \(100 \cdot 9.8 = 980 \text{ N}\) (en el centro, 2.5m).
Persona A en 0m. Persona B en \(5 - 1.5 = 3.5 \text{ m}\).

1. Sumatoria de Torques en A (Pivote en A):

• Peso: \(-980 \cdot 2.5\)
• Persona B: \(+F_B \cdot 3.5\)

\[ -2450 + 3.5 F_B = 0 \Rightarrow F_B = \frac{2450}{3.5} = 700 \text{ N} \]

2. Sumatoria de Fuerzas Verticales:
\[ F_A + F_B = 980 \]
\[ F_A + 700 = 980 \Rightarrow F_A = 280 \text{ N} \]

Resultado: La persona en el extremo carga 280 N y la otra carga 700 N.

Ejercicios Para Practicar

Pon a prueba tus conocimientos resolviendo los siguientes retos.

Descargar Ejercicios de Torque en PDF

¿Necesitas más práctica para tu examen? Hemos preparado un cuadernillo con 20 ejercicios adicionales de estática y torque.

Conclusión