Tiro Parabólico: Fórmulas y 20 Ejercicios Resueltos [PDF]

Imagina a un jugador de fútbol americano lanzando un pase de 40 yardas o un proyectil saliendo de un cañón. La curva que dibujan en el aire no es magia, es física pura. Hoy aprenderás a dominar el Tiro Parabólico (o Movimiento de Proyectiles), combinando lo que sabes de MRU y Caída Libre.

¿Qué es el Tiro Parabólico?

Es un movimiento en dos dimensiones (2D) que ocurre cuando lanzas un objeto con un ángulo de elevación. Lo interesante es que se compone de dos movimientos independientes:

1. Eje Horizontal (X): Es un Movimiento Rectilíneo Uniforme (MRU). La velocidad es constante porque no hay aceleración (despreciamos el aire).
2. Eje Vertical (Y): Es un Tiro Vertical (MRUA) afectado por la gravedad ($g$).

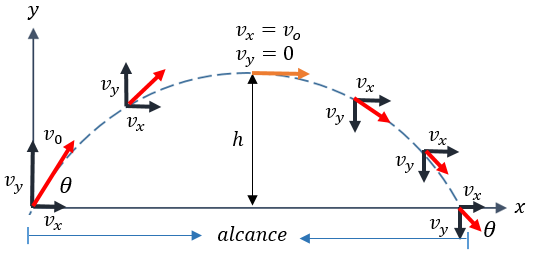
La Independencia de los Movimientos (Galileo)

El gran físico Galileo Galilei fue quien descubrió que en un movimiento parabólico, lo que ocurre en el eje X no afecta lo que ocurre en el eje Y. Esto se conoce como el Principio de Independencia de los Movimientos.

Imagina que dejas caer una moneda y al mismo tiempo lanzas otra horizontalmente. Aunque una viaja hacia adelante, ambas tocarán el suelo al mismo tiempo. Esto sucede porque la gravedad ($g = 9.8 m/s^2$) jala a ambas hacia abajo con la misma intensidad, sin importar qué tan rápido se muevan horizontalmente.

Tipos de Tiro Parabólico (Horizontal vs Oblicuo)

No todos los lanzamientos son iguales. Dependiendo del ángulo inicial ($\theta$), podemos clasificar el movimiento en dos tipos principales:

1. Tiro Parabólico Horizontal (Semiparabólico)

Ocurre cuando el objeto se lanza con un ángulo de 0° (totalmente horizontal) desde cierta altura. Es el caso típico de un avión soltando una caja o una pelota rodando por una mesa hasta caer.

• La velocidad inicial en Y es cero ($v_{0y} = 0$).
• Toda la velocidad inicial pertenece al eje X ($v_{0x} = v_0$).
• Las fórmulas se simplifican mucho.

2. Tiro Parabólico Oblicuo (Completo)

Es el caso general donde el objeto sale del suelo con un ángulo de inclinación (por ejemplo, patear un balón de fútbol). Aquí el objeto sube hasta una altura máxima y luego baja. La trayectoria es una parábola completa y simétrica (si sale y llega a la misma altura).

⭐ Formulario de Tiro Parabólico

Para resolver cualquier problema, primero debes descomponer la velocidad inicial ($v_0$) en sus componentes:

Fórmulas Rápidas (Para Alcance y Altura)

Si el proyectil sale y llega al mismo nivel (suelo a suelo), puedes usar estas fórmulas directas:

• Altura Máxima ($H$):
  \[ H = \frac{(v_0 \sin \theta)^2}{2g} \]
• Alcance Horizontal ($R$):
  \[ R = \frac{v_0^2 \sin(2\theta)}{g} \]
• Tiempo de Vuelo ($t_T$):
  \[ t_T = \frac{2 v_0 \sin \theta}{g} \]

Fórmulas Generales (Posición en cualquier instante)

• Posición en X: \( x = v_{0x} \cdot t \)
• Posición en Y: \( y = v_{0y} \cdot t - \frac{1}{2} g t^2 \)
• Velocidad en Y: \( v_y = v_{0y} - g t \)

Análisis de la Velocidad en la Trayectoria

Es vital entender cómo cambia la velocidad vectorialmente en cada punto:

• Al inicio: La velocidad es máxima. Tiene componentes tanto en X como en Y positivas.
• En la Altura Máxima: Es el punto más lento del recorrido. ¿Por qué? Porque la velocidad vertical desaparece momentáneamente ($v_y = 0$). Sin embargo, la velocidad NO es cero, ya que el objeto sigue avanzando horizontalmente ($v_x$).
• Al caer: El objeto recupera velocidad debido a la gravedad. Si cae al mismo nivel del lanzamiento, llegará con la misma magnitud de velocidad con la que salió, pero con el ángulo invertido.

✅ Ejercicios Resueltos de Tiro Parabólico (Paso a Paso)

Empecemos con los problemas clásicos de examen.

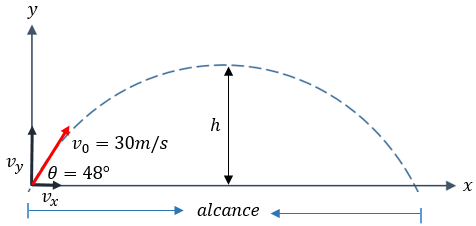
Solución:

Datos: \(v_0 = 30 \text{ m/s}\), \(\theta = 48^\circ\), \(g = 9.8 \text{ m/s}^2\).

a) Altura Máxima ($H$):
\[ H = \frac{(30)^2 (\sin 48^\circ)^2}{2(9.8)} = \frac{900 (0.743)^2}{19.6} \]
\[ H = \frac{900(0.552)}{19.6} = \frac{496.8}{19.6} = 25.35 \text{ m} \]

b) Alcance ($R$):
Usamos el seno del ángulo doble ($2\theta = 96^\circ$):
\[ R = \frac{(30)^2 \sin(96^\circ)}{9.8} = \frac{900(0.994)}{9.8} = 91.33 \text{ m} \]

c) Tiempo de Vuelo ($t_T$):
\[ t_T = \frac{2(30) \sin 48^\circ}{9.8} = \frac{60(0.743)}{9.8} = 4.55 \text{ s} \]

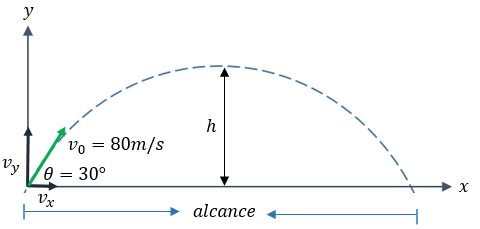
Solución:

Primero descomponemos la velocidad:

\( v_{0x} = 80 \cos 30^\circ = 69.28 \text{ m/s} \)
\( v_{0y} = 80 \sin 30^\circ = 40 \text{ m/s} \)

a) Posición a los 6s:

\( x = (69.28)(6) = 415.68 \text{ m} \)
\( y = (40)(6) - 0.5(9.8)(6)^2 = 240 - 176.4 = 63.6 \text{ m} \)

Velocidad a los 6s:

\( v_y = 40 - (9.8)(6) = 40 - 58.8 = -18.8 \text{ m/s} \) (Va bajando).
Magnitud total: \( v = \sqrt{(69.28)^2 + (-18.8)^2} = 71.79 \text{ m/s} \).

b) Tiempo Altura Máxima ($t_{subida}$):

\[ t = \frac{v_{0y}}{g} = \frac{40}{9.8} = 4.08 \text{ s} \]

c) Alcance Horizontal:

\[ R = v_{0x} \cdot t_{total} = (69.28)(2 \times 4.08) = (69.28)(8.16) = 565.3 \text{ m} \]

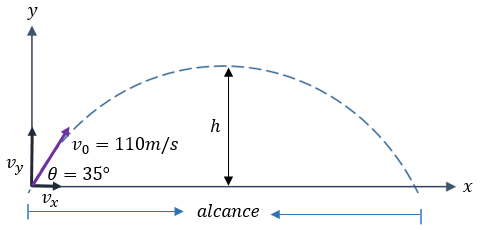
Solución:

a) Alcance ($R$):

\[ R = \frac{(110)^2 \sin(70^\circ)}{9.8} = \frac{12100(0.939)}{9.8} = 1160.6 \text{ m} \]

b) Altura Máxima ($H$):

\[ H = \frac{(110 \sin 35^\circ)^2}{2(9.8)} = \frac{(63.09)^2}{19.6} = \frac{3980}{19.6} = 203 \text{ m} \]

🚀 Ejercicios Avanzados (Nuevos)

Subamos el nivel con problemas que requieren más análisis.

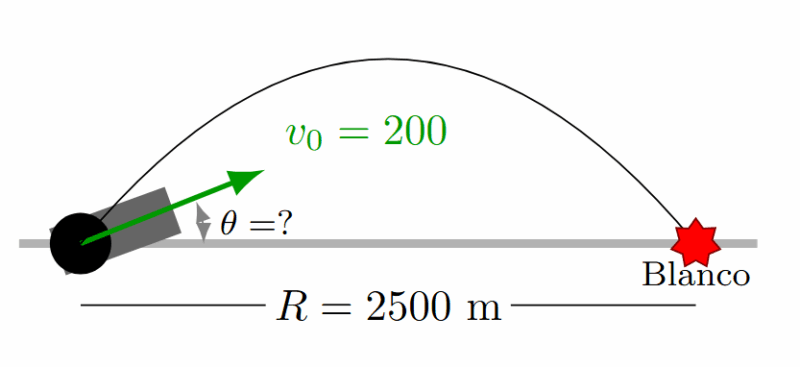
Solución:

Usamos la fórmula del alcance y despejamos \(\theta\):

\[ R = \frac{v_0^2 \sin 2\theta}{g} \Rightarrow \sin 2\theta = \frac{R \cdot g}{v_0^2} \]
\[ \sin 2\theta = \frac{(2500)(9.8)}{(200)^2} = \frac{24500}{40000} = 0.6125 \]
\[ 2\theta = \sin^{-1}(0.6125) = 37.77^\circ \]
\[ \theta = 18.88^\circ \]

Resultado: El ángulo debe ser de 18.88° (o su complementario 71.12°).

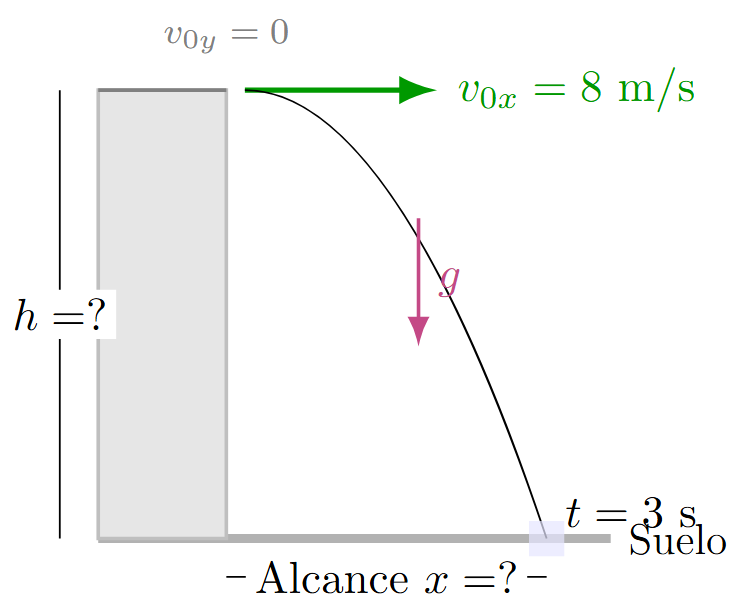
Solución:

En tiro horizontal, el ángulo es 0°, por lo que \(v_{0y} = 0\) y \(v_{0x} = 8 \text{ m/s}\).

Altura (Y):

\[ y = v_{0y}t + \frac{1}{2}gt^2 = 0 + 0.5(9.8)(3)^2 = 44.1 \text{ m} \]

Alcance (X):

\[ x = v_{0x} \cdot t = (8)(3) = 24 \text{ m} \]

Resultado: Altura de 44.1 m y alcance de 24 m.

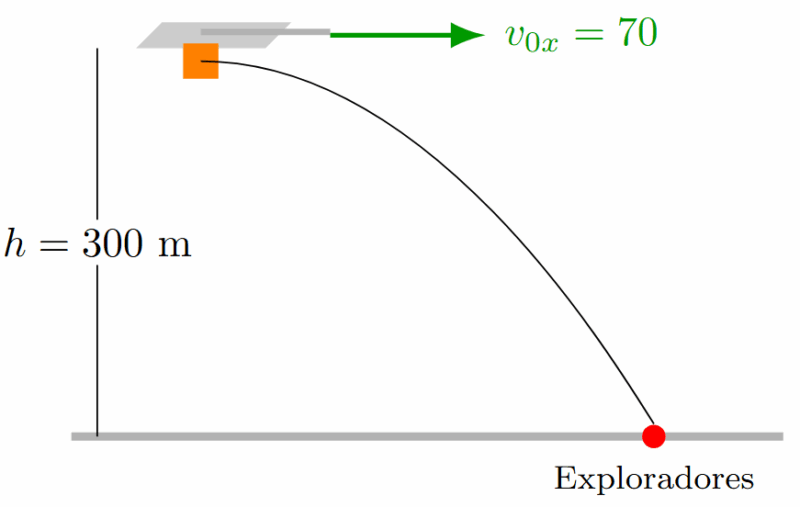
Solución:

Este es un Tiro Semiparabólico (o Tiro Horizontal).
Datos: \(v_{0x} = 70 \text{ m/s}\), \(v_{0y} = 0\), \(h = 300 \text{ m}\).

1. Calculamos el tiempo de caída:

Solo depende de la altura (como en caída libre).

\[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(300)}{9.8}} = \sqrt{61.22} = 7.82 \text{ s} \]

2. Calculamos la distancia horizontal ($x$):

Durante esos 7.82 segundos, el paquete sigue avanzando a la velocidad del avión.

\[ x = v_{0x} \cdot t = (70 \text{ m/s})(7.82 \text{ s}) = 547.4 \text{ m} \]

Resultado: Debe soltarlo 547.4 metros antes de llegar al punto.

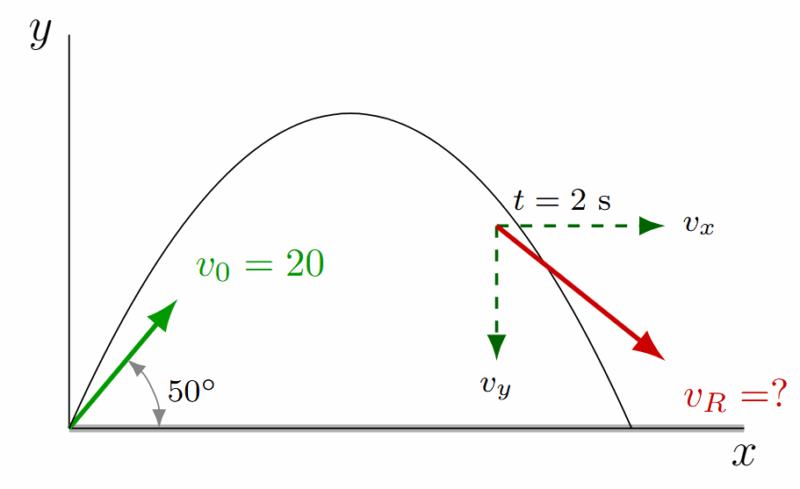
Solución:

La velocidad es un vector, así que debemos calcular sus componentes $v_x$ y $v_y$ a los 2 segundos.

1. Componentes Iniciales:

\[ v_{0x} = 20 \cos 50^\circ = 12.85 \text{ m/s} \]
\[ v_{0y} = 20 \sin 50^\circ = 15.32 \text{ m/s} \]

2. Velocidades a los 2 segundos:

\(v_x\): Permanece constante = 12.85 m/s.
\(v_y\): Se ve afectada por la gravedad.
\[ v_y = v_{0y} - gt = 15.32 - (9.8)(2) = 15.32 - 19.6 = -4.28 \text{ m/s} \]

(El signo negativo indica que la piedra ya va bajando).

3. Magnitud de la Velocidad Resultante:

\[ v_R = \sqrt{(v_x)^2 + (v_y)^2} = \sqrt{(12.85)^2 + (-4.28)^2} \]

\[ v_R = \sqrt{165.12 + 18.31} = \sqrt{183.43} = 13.54 \text{ m/s} \]

Resultado: La velocidad es de 13.54 m/s.

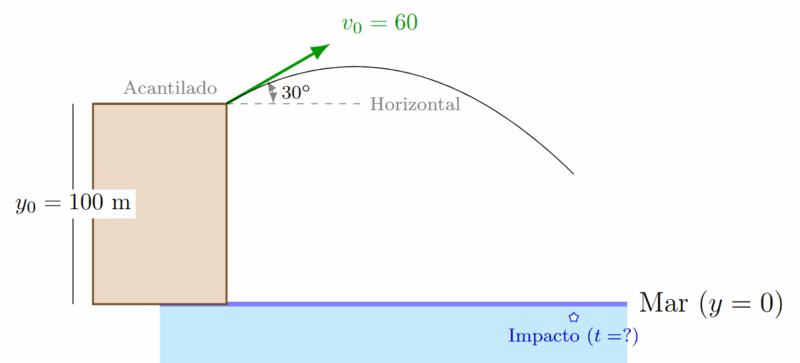
Solución:

Este es un problema avanzado porque el proyectil cae más abajo de donde salió.

Datos: \(h_0 = 100 \text{ m}\) (posición inicial), \(y_{final} = 0 \text{ m}\).

\(v_{0y} = 60 \sin 30^\circ = 30 \text{ m/s}\).

Usamos la ecuación de posición general:

\[ y_f = y_0 + v_{0y}t - \frac{1}{2}gt^2 \]
\[ 0 = 100 + 30t - 4.9t^2 \]

Reordenamos como ecuación cuadrática: \( 4.9t^2 - 30t - 100 = 0 \).

Usamos la Fórmula General \( t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \):

\[ t = \frac{30 \pm \sqrt{(-30)^2 - 4(4.9)(-100)}}{9.8} \]
\[ t = \frac{30 \pm \sqrt{900 + 1960}}{9.8} = \frac{30 \pm \sqrt{2860}}{9.8} \]
\[ t = \frac{30 \pm 53.48}{9.8} \]

Tomamos el tiempo positivo:

\[ t = \frac{83.48}{9.8} = 8.51 \text{ s} \]

Resultado: Tarda 8.51 segundos en caer al mar.

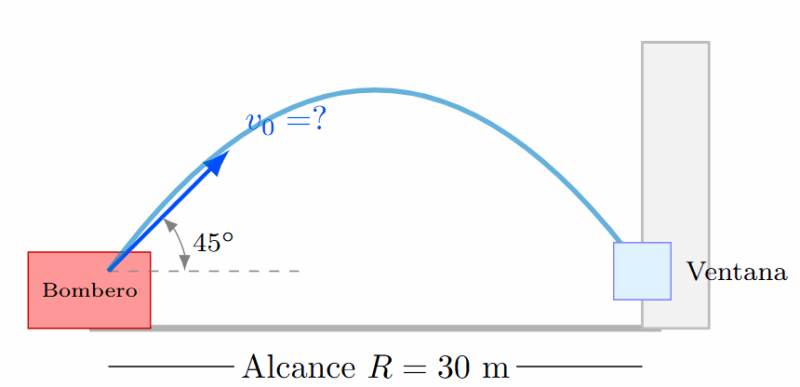
Solución:

Tenemos el Alcance ($R = 30$) y el ángulo ($\theta = 45^\circ$). Buscamos $v_0$.

Fórmula de Alcance:

\[ R = \frac{v_0^2 \sin 2\theta}{g} \]

Despejamos $v_0$:

\[ v_0^2 = \frac{R \cdot g}{\sin 2\theta} \]
Sustituimos ($\sin(90^\circ) = 1$):
\[ v_0^2 = \frac{30 \cdot 9.8}{1} = 294 \]
\[ v_0 = \sqrt{294} = 17.14 \text{ m/s} \]

Resultado: Requiere una velocidad de 17.14 m/s.

Ejercicios Para Practicar

Intenta resolverlos.

Problema Práctico 1: Patriotas NFL

Un jugador patea el balón a 15 m/s con ángulo de 37°. Calcule el tiempo total en el aire y la altura máxima.

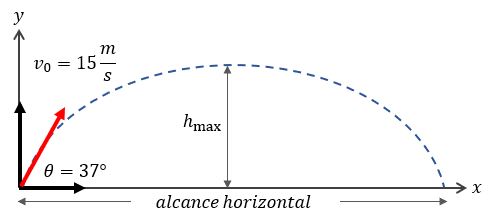
▶︎ Haz clic aquí para ver la solución

\( t_T = \frac{2(15)\sin 37}{9.8} = 1.84 \text{ s} \)
\( H = \frac{(15\sin 37)^2}{19.6} = 4.15 \text{ m} \)

Problema Práctico 2: La Bala

Una bala se lanza a 200 m/s para golpear un blanco a 2500 m. Calcula el tiempo que tarda en llegar con el ángulo menor (18.88°).

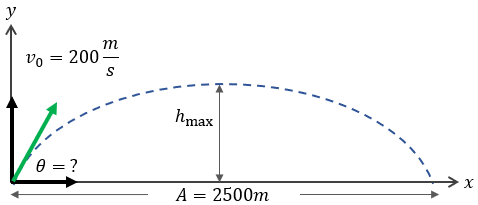
▶︎ Haz clic aquí para ver la solución

\( v_x = 200 \cos 18.88 = 189.3 \text{ m/s} \)
\( t = R / v_x = 2500 / 189.3 = 13.2 \text{ s} \)

Descargar Guía: 20 Ejercicios de Tiro Parabólico [PDF]

¿Quieres problemas con altura inicial diferente o tiro semiparabólico? Descarga nuestra guía. No olvides visitar más problemas de Cinemática.

Examen de Tiro Parabólico

Conclusión

El tiro parabólico combina la independencia de los movimientos horizontal y vertical. Recuerda siempre descomponer tu velocidad inicial antes de empezar a calcular.