Tiro Parabólico: Fórmulas y 20 Ejercicios Resueltos [PDF]
Imagina a un jugador de fútbol americano lanzando un pase de 40 yardas o un proyectil saliendo de un cañón. La curva que dibujan en el aire no es magia, es física pura. Hoy aprenderás a dominar el Tiro Parabólico (o Movimiento de Proyectiles), combinando lo que sabes de MRU y Caída Libre.
¿Qué aprenderás en esta guía?
En este artículo dominarás:
- Las fórmulas de Altura Máxima, Alcance y Tiempo de Vuelo.
- Cómo descomponer la velocidad en sus componentes \(v_x\) y \(v_y\).
- Ejercicios Resueltos paso a paso (Fútbol, Proyectiles y Balas).
- Acceso a nuestra guía PDF con 20 ejercicios.
- ¿Qué es el Tiro Parabólico?
- Tipos de Tiro Parabólico (Horizontal vs Oblicuo)
- ⭐ Formulario de Tiro Parabólico
- ✅ Ejercicios Resueltos de Tiro Parabólico (Paso a Paso)
- 🚀 Ejercicios Avanzados (Nuevos)
- Ejercicios Para Practicar
- Descargar Guía: 20 Ejercicios de Tiro Parabólico [PDF]
- Examen de Tiro Parabólico
- Conclusión
¿Qué es el Tiro Parabólico?
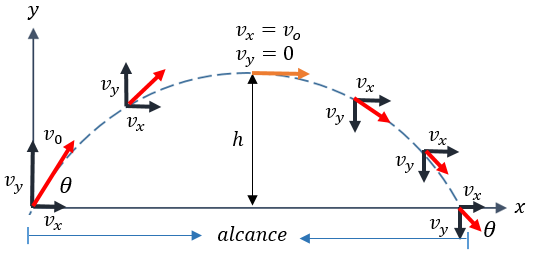
Es un movimiento en dos dimensiones (2D) que ocurre cuando lanzas un objeto con un ángulo de elevación. Lo interesante es que se compone de dos movimientos independientes:
- Eje Horizontal (X): Es un Movimiento Rectilíneo Uniforme (MRU). La velocidad es constante porque no hay aceleración (despreciamos el aire).
- Eje Vertical (Y): Es un Tiro Vertical (MRUA) afectado por la gravedad ($g$).
La Independencia de los Movimientos (Galileo)
El gran físico Galileo Galilei fue quien descubrió que en un movimiento parabólico, lo que ocurre en el eje X no afecta lo que ocurre en el eje Y. Esto se conoce como el Principio de Independencia de los Movimientos.
Imagina que dejas caer una moneda y al mismo tiempo lanzas otra horizontalmente. Aunque una viaja hacia adelante, ambas tocarán el suelo al mismo tiempo. Esto sucede porque la gravedad ($g = 9.8 m/s^2$) jala a ambas hacia abajo con la misma intensidad, sin importar qué tan rápido se muevan horizontalmente.
💡 Dato Clave
En el punto más alto de la trayectoria (Altura Máxima), la velocidad vertical ($v_y$) es CERO. Solo queda la velocidad horizontal ($v_x$).
Tipos de Tiro Parabólico (Horizontal vs Oblicuo)
No todos los lanzamientos son iguales. Dependiendo del ángulo inicial ($\theta$), podemos clasificar el movimiento en dos tipos principales:
1. Tiro Parabólico Horizontal (Semiparabólico)
Ocurre cuando el objeto se lanza con un ángulo de 0° (totalmente horizontal) desde cierta altura. Es el caso típico de un avión soltando una caja o una pelota rodando por una mesa hasta caer.
- La velocidad inicial en Y es cero ($v_{0y} = 0$).
- Toda la velocidad inicial pertenece al eje X ($v_{0x} = v_0$).
- Las fórmulas se simplifican mucho.
2. Tiro Parabólico Oblicuo (Completo)
Es el caso general donde el objeto sale del suelo con un ángulo de inclinación (por ejemplo, patear un balón de fútbol). Aquí el objeto sube hasta una altura máxima y luego baja. La trayectoria es una parábola completa y simétrica (si sale y llega a la misma altura).
⭐ Formulario de Tiro Parabólico
Para resolver cualquier problema, primero debes descomponer la velocidad inicial ($v_0$) en sus componentes:
\[ v_{0x} = v_0 \cos \theta \]
\[ v_{0y} = v_0 \sin \theta \]
Fórmulas Rápidas (Para Alcance y Altura)
Si el proyectil sale y llega al mismo nivel (suelo a suelo), puedes usar estas fórmulas directas:
- Altura Máxima ($H$):
\[ H = \frac{(v_0 \sin \theta)^2}{2g} \] - Alcance Horizontal ($R$):
\[ R = \frac{v_0^2 \sin(2\theta)}{g} \] - Tiempo de Vuelo ($t_T$):
\[ t_T = \frac{2 v_0 \sin \theta}{g} \]
Fórmulas Generales (Posición en cualquier instante)
- Posición en X: \( x = v_{0x} \cdot t \)
- Posición en Y: \( y = v_{0y} \cdot t - \frac{1}{2} g t^2 \)
- Velocidad en Y: \( v_y = v_{0y} - g t \)
Análisis de la Velocidad en la Trayectoria
Es vital entender cómo cambia la velocidad vectorialmente en cada punto:
- Al inicio: La velocidad es máxima. Tiene componentes tanto en X como en Y positivas.
- En la Altura Máxima: Es el punto más lento del recorrido. ¿Por qué? Porque la velocidad vertical desaparece momentáneamente ($v_y = 0$). Sin embargo, la velocidad NO es cero, ya que el objeto sigue avanzando horizontalmente ($v_x$).
- Al caer: El objeto recupera velocidad debido a la gravedad. Si cae al mismo nivel del lanzamiento, llegará con la misma magnitud de velocidad con la que salió, pero con el ángulo invertido.
✅ Ejercicios Resueltos de Tiro Parabólico (Paso a Paso)
Empecemos con los problemas clásicos de examen.
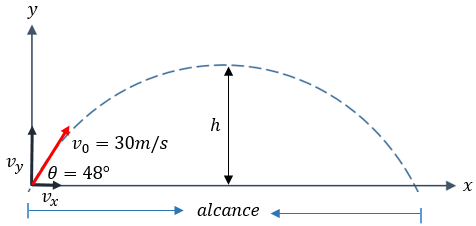
Ejemplo 1: Fútbol Americano
Un jugador de Fútbol Americano patea el balón con una velocidad de 30 m/s, y éste lleva un ángulo de elevación de 48° respecto a la horizontal. Calcule: a) Altura máxima, b) Alcance horizontal, c) Tiempo que permanece en el aire.
Solución:
Datos: \(v_0 = 30 \text{ m/s}\), \(\theta = 48^\circ\), \(g = 9.8 \text{ m/s}^2\).
a) Altura Máxima ($H$):
\[ H = \frac{(30)^2 (\sin 48^\circ)^2}{2(9.8)} = \frac{900 (0.743)^2}{19.6} \]
\[ H = \frac{900(0.552)}{19.6} = \frac{496.8}{19.6} = 25.35 \text{ m} \]
b) Alcance ($R$):
Usamos el seno del ángulo doble ($2\theta = 96^\circ$):
\[ R = \frac{(30)^2 \sin(96^\circ)}{9.8} = \frac{900(0.994)}{9.8} = 91.33 \text{ m} \]
c) Tiempo de Vuelo ($t_T$):
\[ t_T = \frac{2(30) \sin 48^\circ}{9.8} = \frac{60(0.743)}{9.8} = 4.55 \text{ s} \]
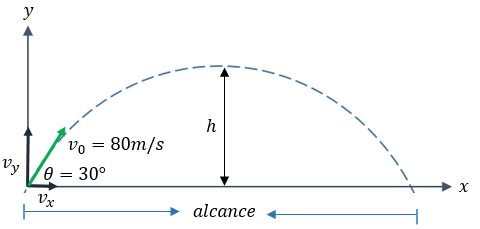
Ejemplo 2: Proyectil a 30 grados
Se dispara un proyectil con una velocidad inicial de 80 m/s y un ángulo de 30°. Calcular: a) Posición y velocidad a los 6s, b) Tiempo para altura máxima, c) Alcance horizontal.
Solución:
Primero descomponemos la velocidad:
\( v_{0x} = 80 \cos 30^\circ = 69.28 \text{ m/s} \)
\( v_{0y} = 80 \sin 30^\circ = 40 \text{ m/s} \)
a) Posición a los 6s:
\( x = (69.28)(6) = 415.68 \text{ m} \)
\( y = (40)(6) - 0.5(9.8)(6)^2 = 240 - 176.4 = 63.6 \text{ m} \)
Velocidad a los 6s:
\( v_y = 40 - (9.8)(6) = 40 - 58.8 = -18.8 \text{ m/s} \) (Va bajando).
Magnitud total: \( v = \sqrt{(69.28)^2 + (-18.8)^2} = 71.79 \text{ m/s} \).
b) Tiempo Altura Máxima ($t_{subida}$):
\[ t = \frac{v_{0y}}{g} = \frac{40}{9.8} = 4.08 \text{ s} \]
c) Alcance Horizontal:
\[ R = v_{0x} \cdot t_{total} = (69.28)(2 \times 4.08) = (69.28)(8.16) = 565.3 \text{ m} \]
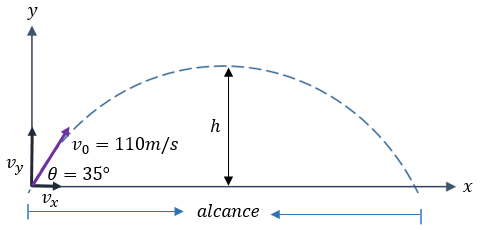
Ejemplo 3: Máquina Lanzadora
Una máquina lanza un proyectil a 110 m/s con ángulo de 35°. Calcular: a) Alcance logrado, b) Altura máxima.
Solución:
a) Alcance ($R$):
\[ R = \frac{(110)^2 \sin(70^\circ)}{9.8} = \frac{12100(0.939)}{9.8} = 1160.6 \text{ m} \]
b) Altura Máxima ($H$):
\[ H = \frac{(110 \sin 35^\circ)^2}{2(9.8)} = \frac{(63.09)^2}{19.6} = \frac{3980}{19.6} = 203 \text{ m} \]
🚀 Ejercicios Avanzados (Nuevos)
Subamos el nivel con problemas que requieren más análisis.
Ejemplo 4: Tiro con Blanco Distante
Una bala de cañón se lanza con \(v_0 = 200 \text{ m/s}\). Si se desea golpear un blanco a 2500 m, ¿cuál es el ángulo de disparo?
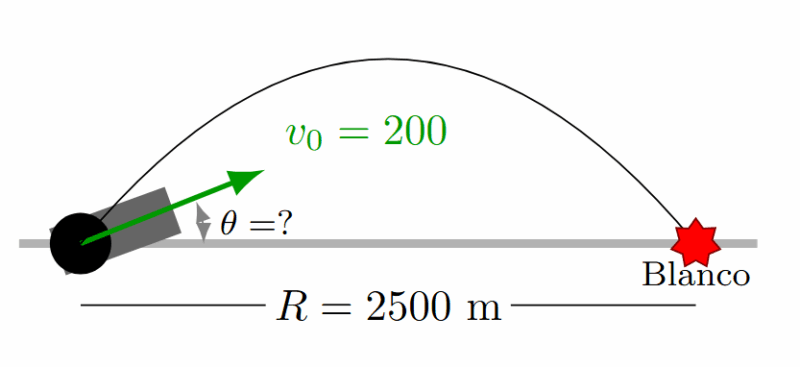
Solución:
Usamos la fórmula del alcance y despejamos \(\theta\):
\[ R = \frac{v_0^2 \sin 2\theta}{g} \Rightarrow \sin 2\theta = \frac{R \cdot g}{v_0^2} \]
\[ \sin 2\theta = \frac{(2500)(9.8)}{(200)^2} = \frac{24500}{40000} = 0.6125 \]
\[ 2\theta = \sin^{-1}(0.6125) = 37.77^\circ \]
\[ \theta = 18.88^\circ \]
Resultado: El ángulo debe ser de 18.88° (o su complementario 71.12°).
Ejemplo 5: Altura de un Edificio (Tiro Horizontal)
Desde la azotea de un edificio se lanza una piedra horizontalmente a 8 m/s. Si tarda 3 segundos en tocar el suelo, ¿cuál es la altura del edificio y a qué distancia de la base cae?
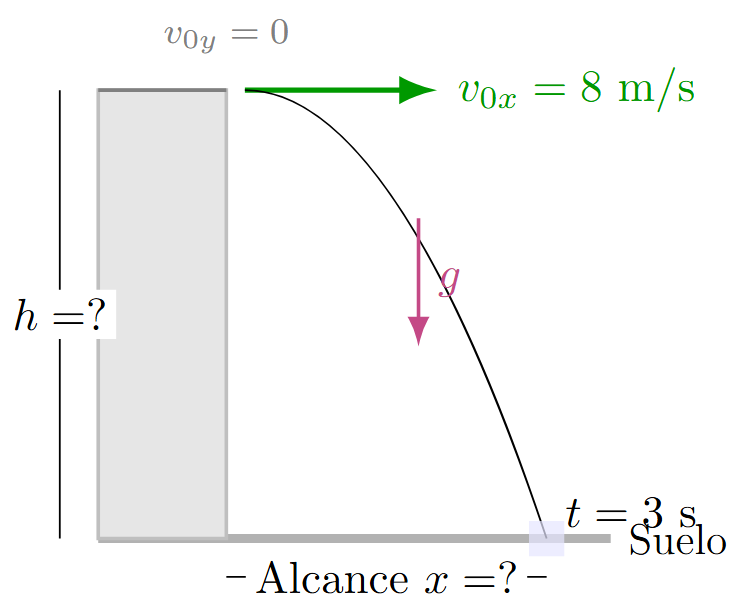
Solución:
En tiro horizontal, el ángulo es 0°, por lo que \(v_{0y} = 0\) y \(v_{0x} = 8 \text{ m/s}\).
Altura (Y):
\[ y = v_{0y}t + \frac{1}{2}gt^2 = 0 + 0.5(9.8)(3)^2 = 44.1 \text{ m} \]
Alcance (X):
\[ x = v_{0x} \cdot t = (8)(3) = 24 \text{ m} \]
Resultado: Altura de 44.1 m y alcance de 24 m.
Ejemplo 6: El Avión de Rescate (Tiro Semiparabólico)
Un avión de rescate vuela horizontalmente a una velocidad de 70 m/s y una altura de 300 m. Debe soltar un paquete de provisiones a un grupo de exploradores. ¿A qué distancia horizontal del objetivo debe soltar el paquete para que caiga justo en el lugar?
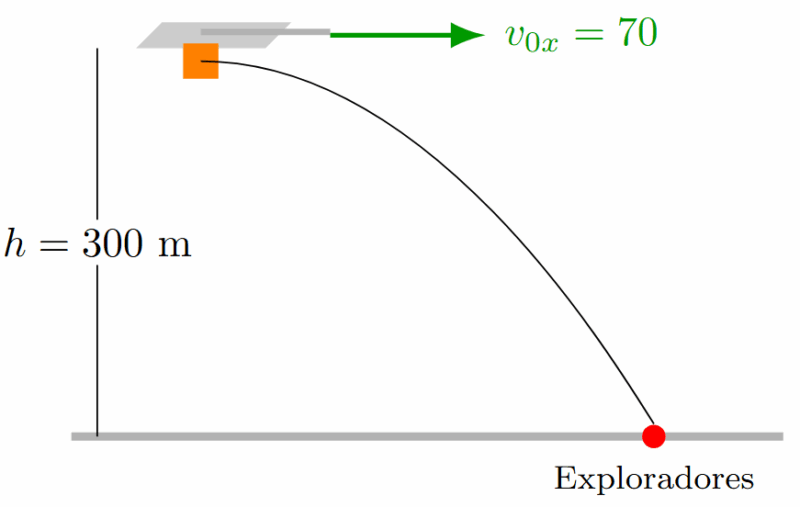
Solución:
Este es un Tiro Semiparabólico (o Tiro Horizontal).
Datos: \(v_{0x} = 70 \text{ m/s}\), \(v_{0y} = 0\), \(h = 300 \text{ m}\).
1. Calculamos el tiempo de caída:
Solo depende de la altura (como en caída libre).
\[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(300)}{9.8}} = \sqrt{61.22} = 7.82 \text{ s} \]
2. Calculamos la distancia horizontal ($x$):
Durante esos 7.82 segundos, el paquete sigue avanzando a la velocidad del avión.
\[ x = v_{0x} \cdot t = (70 \text{ m/s})(7.82 \text{ s}) = 547.4 \text{ m} \]
Resultado: Debe soltarlo 547.4 metros antes de llegar al punto.
Ejemplo 7: Velocidad de Impacto (Vectorial)
Se lanza una piedra con una velocidad inicial de 20 m/s y un ángulo de 50°. Calcule la magnitud de la velocidad (velocidad final) justo 2 segundos después del lanzamiento.
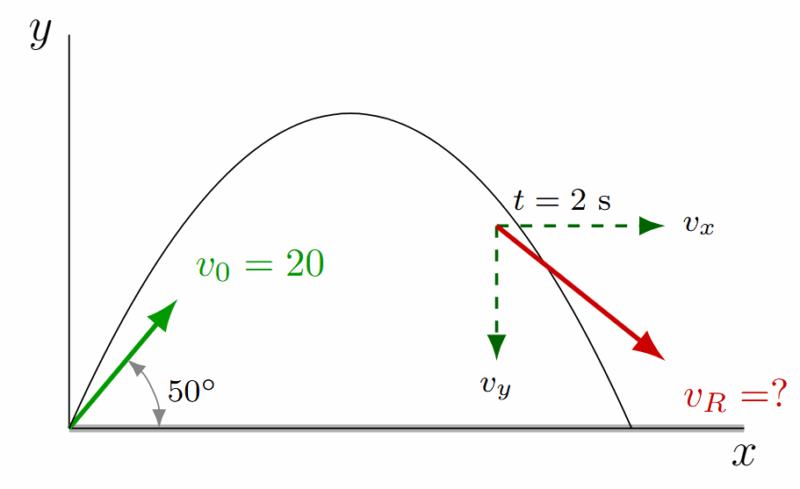
Solución:
La velocidad es un vector, así que debemos calcular sus componentes $v_x$ y $v_y$ a los 2 segundos.
1. Componentes Iniciales:
\[ v_{0x} = 20 \cos 50^\circ = 12.85 \text{ m/s} \]
\[ v_{0y} = 20 \sin 50^\circ = 15.32 \text{ m/s} \]
2. Velocidades a los 2 segundos:
\(v_x\): Permanece constante = 12.85 m/s.
\(v_y\): Se ve afectada por la gravedad.
\[ v_y = v_{0y} - gt = 15.32 - (9.8)(2) = 15.32 - 19.6 = -4.28 \text{ m/s} \]
(El signo negativo indica que la piedra ya va bajando).
3. Magnitud de la Velocidad Resultante:
\[ v_R = \sqrt{(v_x)^2 + (v_y)^2} = \sqrt{(12.85)^2 + (-4.28)^2} \]
\[ v_R = \sqrt{165.12 + 18.31} = \sqrt{183.43} = 13.54 \text{ m/s} \]
Resultado: La velocidad es de 13.54 m/s.
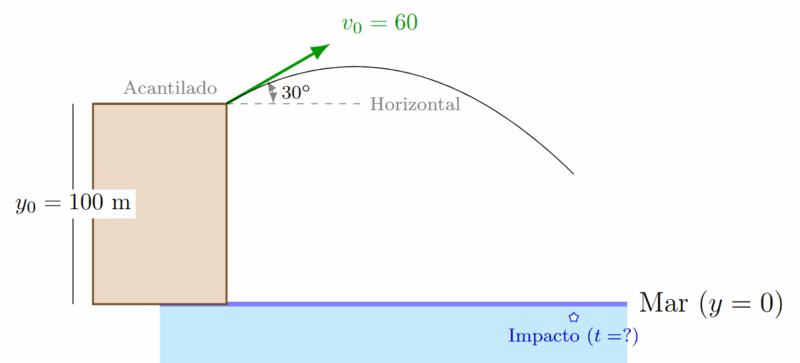
Ejemplo 8: Tiro desde un Acantilado (Con Ángulo)
Un cañón situado en el borde de un acantilado de 100 metros de altura dispara un proyectil con una velocidad de 60 m/s y un ángulo de 30° por encima de la horizontal. ¿Cuánto tiempo tarda en impactar el mar?
Solución:
Este es un problema avanzado porque el proyectil cae más abajo de donde salió.
Datos: \(h_0 = 100 \text{ m}\) (posición inicial), \(y_{final} = 0 \text{ m}\).
\(v_{0y} = 60 \sin 30^\circ = 30 \text{ m/s}\).
Usamos la ecuación de posición general:
\[ y_f = y_0 + v_{0y}t - \frac{1}{2}gt^2 \]
\[ 0 = 100 + 30t - 4.9t^2 \]
Reordenamos como ecuación cuadrática: \( 4.9t^2 - 30t - 100 = 0 \).
Usamos la Fórmula General \( t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \):
\[ t = \frac{30 \pm \sqrt{(-30)^2 - 4(4.9)(-100)}}{9.8} \]
\[ t = \frac{30 \pm \sqrt{900 + 1960}}{9.8} = \frac{30 \pm \sqrt{2860}}{9.8} \]
\[ t = \frac{30 \pm 53.48}{9.8} \]
Tomamos el tiempo positivo:
\[ t = \frac{83.48}{9.8} = 8.51 \text{ s} \]
Resultado: Tarda 8.51 segundos en caer al mar.
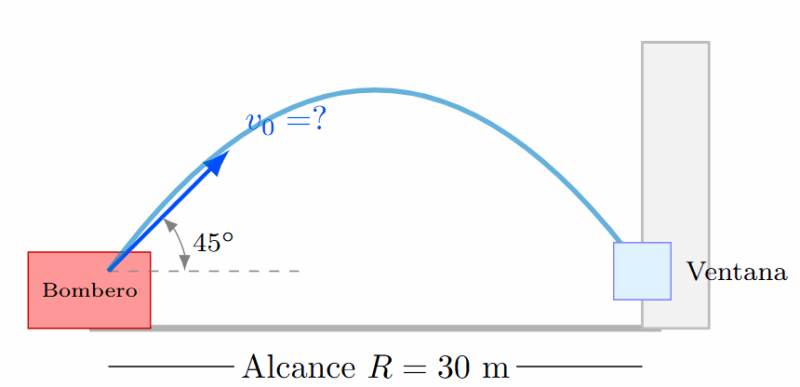
Ejemplo 9: Los Bomberos (Alcance Inverso)
Una manguera de bomberos lanza agua con un ángulo de 45° (ángulo de alcance máximo). Si el agua debe llegar a una ventana situada a 30 metros de distancia horizontal (al mismo nivel), ¿con qué velocidad inicial debe salir el agua?
Solución:
Tenemos el Alcance ($R = 30$) y el ángulo ($\theta = 45^\circ$). Buscamos $v_0$.
Fórmula de Alcance:
\[ R = \frac{v_0^2 \sin 2\theta}{g} \]
Despejamos $v_0$:
\[ v_0^2 = \frac{R \cdot g}{\sin 2\theta} \]
Sustituimos ($\sin(90^\circ) = 1$):
\[ v_0^2 = \frac{30 \cdot 9.8}{1} = 294 \]
\[ v_0 = \sqrt{294} = 17.14 \text{ m/s} \]
Resultado: Requiere una velocidad de 17.14 m/s.
Ejercicios Para Practicar
Intenta resolverlos.
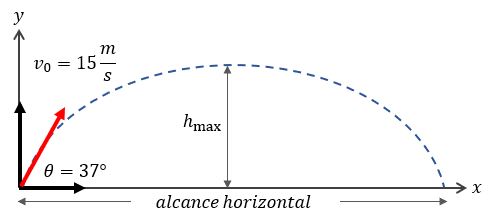
Problema Práctico 1: Patriotas NFL
Un jugador patea el balón a 15 m/s con ángulo de 37°. Calcule el tiempo total en el aire y la altura máxima.
▶︎ Haz clic aquí para ver la solución
\( t_T = \frac{2(15)\sin 37}{9.8} = 1.84 \text{ s} \)
\( H = \frac{(15\sin 37)^2}{19.6} = 4.15 \text{ m} \)
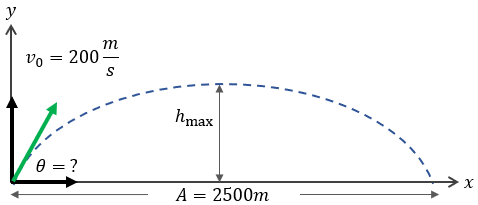
Problema Práctico 2: La Bala
Una bala se lanza a 200 m/s para golpear un blanco a 2500 m. Calcula el tiempo que tarda en llegar con el ángulo menor (18.88°).
▶︎ Haz clic aquí para ver la solución
\( v_x = 200 \cos 18.88 = 189.3 \text{ m/s} \)
\( t = R / v_x = 2500 / 189.3 = 13.2 \text{ s} \)
Descargar Guía: 20 Ejercicios de Tiro Parabólico [PDF]
¿Quieres problemas con altura inicial diferente o tiro semiparabólico? Descarga nuestra guía. No olvides visitar más problemas de Cinemática.
🔒 Incluye Ejercicios de Examen y Gráficas • 100% Gratis
Examen de Tiro Parabólico
Cargando examen...
Conclusión
El tiro parabólico combina la independencia de los movimientos horizontal y vertical. Recuerda siempre descomponer tu velocidad inicial antes de empezar a calcular.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Me podrían ayudar con estos ejercicios por favor.
- sobre la horizontal, con una velocidad de 30m/s. Calcule la altura máxima que alcanza la pelota.
- sobre la superficie de la Tierra, con una velocidad de 15m/s. Calcule el tiempo que dura la flecha en el aire.Es súper urgente por favor...!!
-
Un niño lanza un balón al aro de un tablero de basquetbol, cuya altura es 3,05m.
La distancia horizontal entre el niño y el aro es de 5m. El ángulo con que el niño
lanza el balón es de 60°, y al estirar las manos alcanza 135 cm. El balón alcanza su
altura máxima justo al llegar al aro. a) ¿Con qué velocidad vertical inicial debe
lanzarse el balón? b) ¿Cuánto tarda el balón en el aire desde que sale de las manos
del chico hasta que toca el aro? c) ¿Qué velocidad horizontal tendrá el balón? d)
¿Cuál será la velocidad inicial del balón? Ayuda: en el punto “d” usar el Teorema
de Pitágoras. -
Un artículo muy útil y práctico, muchas gracias.
Lo único que juzgo es que esperaba más ejercicios de práctica y con más grado de dificultad, en cuanto a lo demás, todo me fue muy útil. -
hillaryO
ayer
Física
Universidad
+5 ptos
Dos poleas de 25 y 40 cm de radio respectivamente, giran conectadas por una banda, si la frecuencia de la polea de mayor radio da 18 Vuelt/sg,¿cuál será la frecuencia de la polea de menor radio? * -
Una manzana es lanzada con un ángulo de 45° con la horizontal. Sabiendo que alcanzó 8m como altura máxima, encontrar el alcanza horizontal. Nota: Trabajar con gravedad de 10 m/s²
Por favor ayuden.
123 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar