Variables, Constantes y Coeficientes en Álgebra
¡Hola de nuevo! Ya hemos establecido qué es el álgebra y cómo se forma su lenguaje básico. Ahora, es momento de profundizar en los elementos que dan vida a las expresiones algebraicas: las variables, las constantes y los coeficientes. Entender a fondo cada uno de estos componentes es crucial, ya que son los pilares sobre los que construirás cualquier operación o problema algebraico.
En este artículo, desglosaremos la función de cada uno, cómo identificarlos y por qué su correcta comprensión es fundamental para manipular y resolver ecuaciones. ¡Prepárate para consolidar tu conocimiento del lenguaje algebraico! 🤓
Variables: Las Letras del Álgebra
En álgebra, una variable es un símbolo, usualmente una letra (como $x, y, z, a, b, n, t$, etc.), que representa una cantidad que puede cambiar o un valor desconocido. Son el corazón del álgebra, permitiéndonos formular expresiones y ecuaciones que representan relaciones generales en lugar de casos específicos.
Características Clave de las Variables:
- Representan valores desconocidos: Cuando no sabemos el valor exacto de una cantidad en un problema, usamos una variable para representarla. Por ejemplo, en "un número más 5 es igual a 12", el "número" es una cantidad desconocida que representamos con una variable ($x + 5 = 12$).
- Representan valores que varían: En una fórmula, las variables pueden tomar diferentes valores. Por ejemplo, en la fórmula del área de un rectángulo ($A = lw$), $l$ (largo) y $w$ (ancho) son variables porque pueden cambiar para diferentes rectángulos.
- Versatilidad: Las variables pueden representar cualquier tipo de número (enteros, decimales, fracciones, etc.).
Ejemplos de Uso de Variables:
- Si hablamos de la edad de una persona que cambia con el tiempo, podemos usar la variable $e$ para la edad.
- Para representar una cantidad cualquiera de manzanas, podríamos usar $m$.
- En física, $v$ a menudo representa la velocidad, y $t$ el tiempo.
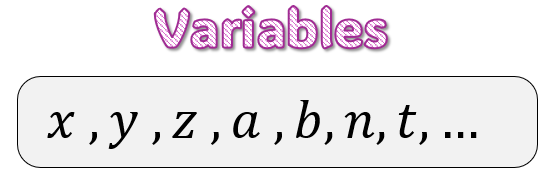
Constantes: Valores Fijos e Inmutables
A diferencia de las variables, una constante es un valor fijo y conocido que no cambia. En una expresión algebraica, las constantes son los números por sí solos, sin ninguna variable asociada a ellos.
Características Clave de las Constantes:
- Valor fijo: Su valor es inmutable y ya está determinado.
- Término independiente: En un polinomio, el término que solo es un número (sin variables) se conoce como término constante o término independiente.
- Números específicos: Incluyen números enteros, decimales, fracciones o incluso valores irracionales como $\pi$ (Pi) o $e$ (número de Euler).
Ejemplos de Uso de Constantes:
- En la expresión $3x + 7$, el $7$ es una constante.
- En la fórmula del perímetro de un círculo $C = 2\pi r$, el $2$ y $\pi$ son constantes.
- En la ecuación $y = mx + b$, si estamos hablando de una línea específica, $b$ es la constante que representa la intersección con el eje $y$.
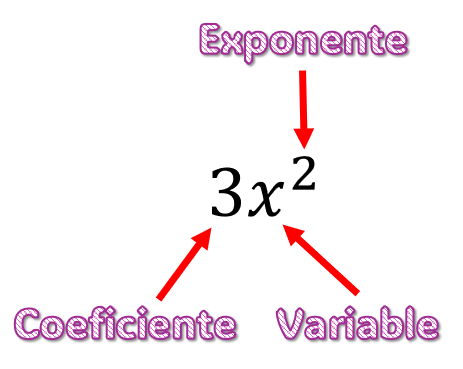
Coeficientes: Los Multiplicadores de las Variables
Un coeficiente es el factor numérico que multiplica a una variable o a un grupo de variables en un término algebraico. Nos indica cuántas veces la variable o el grupo de variables está presente en el término.
Características Clave de los Coeficientes:
- Factor numérico: Siempre es un número (puede ser entero, fraccionario, decimal, positivo o negativo).
- Multiplicador: Indica una multiplicación con la variable o parte literal.
- Parte de un término: El coeficiente es la parte numérica de un término, mientras que la variable(s) es la parte literal.
- Si una variable aparece sola, su coeficiente es $1$. Por ejemplo, en $x$, el coeficiente es $1$. En $-y$, el coeficiente es $-1$.
Ejemplos de Uso de Coeficientes:
- En el término $5x$, el $5$ es el coeficiente de $x$. Significa que tenemos $5$ veces $x$.
- En el término $-3y^2$, el $-3$ es el coeficiente de $y^2$.
- En el término $\frac{1}{2}ab$, el $\frac{1}{2}$ es el coeficiente de $ab$.
- En el término $z$, el coeficiente es $1$.
- En el término $-m$, el coeficiente es $-1$.
Diferencias Clave y Relación entre ellos
Es fundamental distinguir entre estos tres elementos:
- Una variable ($x$) representa una cantidad que puede cambiar o es desconocida.
- Una constante ($7$) es un valor fijo y conocido.
- Un coeficiente ($5$ en $5x$) es el número que multiplica a la variable en un término.
En una expresión como $4x + 9$, $x$ es la variable, $4$ es el coeficiente de $x$, y $9$ es la constante (o término independiente).
Ejercicios Resueltos
Problema 1. En la expresión algebraica $7y^3 - 2x + 15$, identifica las variables, los coeficientes y las constantes.
Solución
▷ Paso 1 Identificar las variables.
Las letras presentes en la expresión son $y$ y $x$.
Variables: $x, y$.
▷ Paso 2 Identificar los coeficientes.
El coeficiente del término $7y^3$ es $7$.
El coeficiente del término $-2x$ es $-2$.
Coeficientes: $7, -2$.
▷ Paso 3 Identificar las constantes.
El número que no está acompañado por ninguna variable es $15$.
Constantes: $15$.
Problema 2. Dada la ecuación $5a - 8 = 2b + 1$, ¿cuáles son las variables? ¿Hay alguna constante en el lado izquierdo de la ecuación? ¿Y en el lado derecho?
Solución
▷ Paso 1 Identificar las variables.
Las letras utilizadas en la ecuación son $a$ y $b$.
Variables: $a, b$.
▷ Paso 2 Identificar las constantes en el lado izquierdo.
En el lado izquierdo ($5a - 8$), el número sin variable es $-8$.
Constante en el lado izquierdo: $-8$.
▷ Paso 3 Identificar las constantes en el lado derecho.
En el lado derecho ($2b + 1$), el número sin variable es $1$.
Constante en el lado derecho: $1$.
Problema 3. Para la expresión $x^2 - 4xy + y^3 - 1$, indica el coeficiente de cada término con variable y la constante.
Solución
▷ Paso 1 Identificar los términos con variables y sus coeficientes.
Término $x^2$: No hay número visible, por lo que el coeficiente es $1$.
Coeficiente de $x^2$: $1$.
▷ Paso 2 Identificar el coeficiente del segundo término.
Término $-4xy$: El número que multiplica a $xy$ es $-4$.
Coeficiente de $xy$: $-4$.
▷ Paso 3 Identificar el coeficiente del tercer término.
Término $y^3$: No hay número visible, por lo que el coeficiente es $1$.
Coeficiente de $y^3$: $1$.
▷ Paso 4 Identificar la constante.
El término que no tiene variable es $-1$.
Constante: $-1$.
Problema 4. En la fórmula del área de un triángulo $A = \frac{1}{2}bh$, ¿cuáles son las variables y cuáles son las constantes (asumiendo que $A, b, h$ pueden variar para diferentes triángulos)?
Solución
▷ Paso 1 Identificar las variables.
Las letras que representan cantidades que pueden cambiar son $A$ (área), $b$ (base) y $h$ (altura).
Variables: $A, b, h$.
▷ Paso 2 Identificar las constantes.
El valor numérico fijo en la fórmula es $\frac{1}{2}$.
Constantes: $\frac{1}{2}$.
Problema 5. La expresión para el costo total de producir $q$ unidades de un producto es $C = 15q + 200$. Identifica el coeficiente y la constante en esta expresión.
Solución
▷ Paso 1 Identificar el coeficiente.
El número que multiplica a la variable $q$ es $15$.
Coeficiente: $15$.
▷ Paso 2 Identificar la constante.
El término que no tiene variable es $200$.
Constante: $200$.
Problema 6. Escribe una expresión algebraica que contenga una variable $p$ con coeficiente $3$, una variable $q$ con coeficiente $-1$, y una constante de $8$.
Solución
▷ Paso 1 Escribir el término con la variable $p$ y su coeficiente.
Variable $p$, coeficiente $3$: $3p$.
▷ Paso 2 Escribir el término con la variable $q$ y su coeficiente.
Variable $q$, coeficiente $-1$: $-1q$ o simplemente $-q$.
▷ Paso 3 Añadir la constante.
La constante es $8$.
▷ Paso 4 Combinar todos los términos para formar la expresión.
La expresión es: $$3p - q + 8$$
Problema 7. En la expresión que representa la cantidad de dinero que tienes: "Tengo $m$ billetes de $50 y $n$ billetes de $20". Escribe la expresión y luego identifica las variables, constantes y coeficientes.
Solución
▷ Paso 1 Escribir la expresión algebraica.
La cantidad de dinero de billetes de $$50$ es $50m$.
La cantidad de dinero de billetes de $$20$ es $20n$.
La expresión total es la suma de estas cantidades: $$50m + 20n$$
▷ Paso 2 Identificar las variables.
Las letras que representan cantidades de billetes (que pueden variar) son $m$ y $n$.
Variables: $m, n$.
▷ Paso 3 Identificar los coeficientes.
El coeficiente de $m$ es $50$ (el valor del billete).
El coeficiente de $n$ es $20$ (el valor del billete).
Coeficientes: $50, 20$.
▷ Paso 4 Identificar las constantes.
En esta expresión, no hay un término numérico que no esté multiplicando una variable.
Constantes: No hay constantes explícitas en esta expresión.
Problema 8. La temperatura en grados Celsius, $C$, se convierte a grados Fahrenheit, $F$, usando la fórmula $F = \frac{9}{5}C + 32$. Identifica las variables y las constantes en esta fórmula.
Solución
▷ Paso 1 Identificar las variables.
Las cantidades que pueden cambiar (las temperaturas) son $F$ y $C$.
Variables: $F, C$.
▷ Paso 2 Identificar las constantes.
Los valores numéricos fijos en la fórmula son $\frac{9}{5}$ (que es el coeficiente de $C$) y $32$.
Constantes: $\frac{9}{5}, 32$.
Conclusión
Hemos recorrido los conceptos esenciales de variables, constantes y coeficientes, comprendiendo su rol único en la formación del lenguaje algebraico. Las variables nos dan la flexibilidad para generalizar, las constantes anclan nuestras expresiones a valores fijos, y los coeficientes nos indican la magnitud de las variables.
Dominar la identificación y el significado de estos componentes no solo te permitirá leer y escribir expresiones algebraicas con fluidez, sino que también te sentará una base sólida para las operaciones que veremos a continuación, como la simplificación de expresiones y la resolución de ecuaciones. ¡Sigue practicando y consolidando estos conceptos, son la clave de tu éxito en el álgebra!
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta
Estos temas te pueden interesar