Derivada de Funciones Trigonométricas Inversas

Derivadas Inversas Trigonométricas

Hasta este momento cualquier estudiante debe de estar familiarizado con el uso de las fórmulas de derivación que hemos visto a lo largo de varios artículos de derivadas resueltas paso a paso, ya que las derivadas de funciones trigonométricas inversas implicará conocer las reglas básicas de derivación. ¡Recuerde que puede recurrir a ver nuevamente los ejemplos para asegurarse del conocimiento adquirido!.

Contenidos

Fórmulas de Derivación de Funciones Trigonométricas Inversas
Gráfica de las funciones Trigonométricas Inversas
Derivadas Trigonométricas Inversas Resueltas

Fórmulas de Derivación de Funciones Trigonométricas Inversas

Las siguientes fórmulas son las que emplearemos en los siguientes ejemplos resueltos.

$\displaystyle \frac{d}{dx}arcsen\,u=\frac{\frac{du}{dx}}{\sqrt{1-{{u}^{2}}}}$

$\displaystyle \frac{d}{dx}\arccos \,u=-\frac{\frac{du}{dx}}{\sqrt{1-{{u}^{2}}}}$

$\displaystyle \frac{d}{dx}\arctan \,u=\frac{\frac{du}{dx}}{{{u}^{2}}+1}$

$\displaystyle \frac{d}{dx}arc\cot \,u=-\frac{\frac{du}{dx}}{{{u}^{2}}+1}$

$\displaystyle \frac{d}{dx}arc\sec \,u=\frac{\frac{du}{dx}}{u\sqrt{{{u}^{2}}-1}}$

$\displaystyle \frac{d}{dx}arc\csc \,u=-\frac{\frac{du}{dx}}{u\sqrt{{{u}^{2}}-1}}$

Es momento de realizar algunos ejercicios.

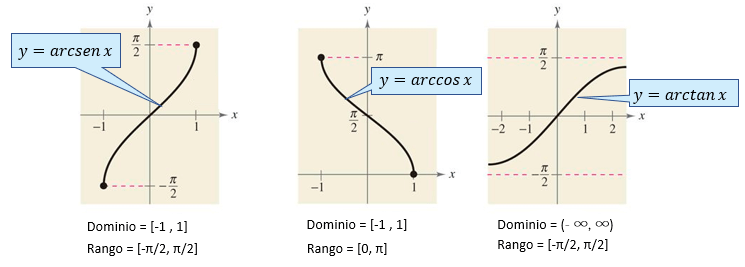
Gráfica de las funciones Trigonométricas Inversas

Gráfica de Funciones Trigonométricas Inversas

Derivadas Trigonométricas Inversas Resueltas

Ejemplo 1. Resuelva la siguiente derivada

$\displaystyle y=arcsen\left( {{x}^{3}}-{{x}^{2}}+1 \right)$

Solución:

Para este ejemplo observamos que nuestro argumento es u = x³-x²+1 , aplicando la fórmula esto nos quedaría:

$\displaystyle y'=\frac{\frac{d}{dx}\left( {{x}^{3}}-{{x}^{2}}+1 \right)}{\sqrt{1-{{\left( {{x}^{3}}-{{x}^{2}}+1 \right)}^{2}}}}$

Que al resolver la derivada, finalmente obtenemos:

Resultado:

$\displaystyle y'=\frac{3{{x}^{2}}-2x}{\sqrt{1-{{\left( {{x}^{3}}-{{x}^{2}}+1 \right)}^{2}}}}$

Ejemplo 2. Resuelva la siguiente derivada

$\displaystyle y=\arctan \sqrt{x}$

Solución:

En este caso, nuestro argumento es u = √x , aplicando nuestra fórmula de derivada para el arco tangente tenemos.

$\displaystyle y'=\frac{\frac{d}{dx}\sqrt{x}}{{{\left( \sqrt{x} \right)}^{2}}+1}$

Derivando la raíz cuadrada:

$\displaystyle y'=\frac{\frac{1}{2\sqrt{x}}}{{{\left( \sqrt{x} \right)}^{2}}+1}=\frac{\frac{1}{2\sqrt{x}}}{x+1}$

Aplicando la ley de la herradura (división de cocientes).

Resultado:

$\displaystyle y'=\frac{1}{2\sqrt{x}\left( x+1 \right)}$

Ejemplo 3. Resuelva la siguiente derivada

$\displaystyle y=arc\sec \left( \frac{1}{x} \right)$

Solución:

Observamos que nuestro argumento es u = 1/x , pero escribiéndola en su forma recíproca esto es x¯ ¹, aplicando la fórmula tenemos:

$\displaystyle y'=\frac{\frac{d}{dx}\left( {{x}^{-1}} \right)}{{{x}^{-1}}\sqrt{{{\left( {{x}^{-1}} \right)}^{2}}-1}}$

Derivando la parte del numerador, tenemos:

$\displaystyle y'=\frac{-{{x}^{-2}}}{{{x}^{-1}}\sqrt{{{\left( {{x}^{-1}} \right)}^{2}}-1}}$

Ordenando el numerador en su forma recíproca.

$\displaystyle y'=\frac{-\frac{1}{{{x}^{2}}}}{\frac{1}{x}\sqrt{\frac{1}{{{x}^{2}}}-1}}$

Hasta este punto ya está derivada la función, sin embargo es bueno arreglar la función aplicando un poco de álgebra.

$\displaystyle y'=\frac{-\frac{1}{{{x}^{2}}}}{\frac{1}{x}\sqrt{\frac{1}{{{x}^{2}}}-1}}=\frac{-x}{{{x}^{2}}\sqrt{\frac{1-{{x}^{2}}}{{{x}^{2}}}}}=-\frac{1}{x\left( \frac{\sqrt{1-{{x}^{2}}}}{\sqrt{{{x}^{2}}}} \right)}$

Simplificando. . .

Resultado:

$\displaystyle y'=-\frac{1}{\sqrt{1-{{x}^{2}}}}$

Ejemplo 4. Resuelva la siguiente derivada

$\displaystyle y={{\left[ \arccos \left( 2x-4 \right) \right]}^{4}}$

Solución:

Para este ejemplo es lógico observar que nuestro argumento es u = arc cos (2x - 4), porque todo está elevado a la cuarta. Entonces primero vamos a derivar como una potencia, de esta forma.

$\displaystyle y'=4{{\left[ \arccos \left( 2x-4 \right) \right]}^{4-1}}\frac{d}{dx}\arccos \left( 2x-4 \right)$

Observamos que la derivada del arco coseno está dentro de la derivada de la potencia, entonces tenemos que seguir las reglas de derivación para el arco coseno.

$\displaystyle y'=4{{\left[ \arccos \left( 2x-4 \right) \right]}^{3}}\left[ -\frac{\frac{d}{dx}\left( 2x-4 \right)}{\sqrt{1-{{\left( 2x-4 \right)}^{2}}}} \right]$

Vemos que existen nuevo argumento, diferente al argumento de la derivada principal. Posteriormente tenemos:

$\displaystyle y'=4{{\left[ \arccos \left( 2x-4 \right) \right]}^{3}}\left[ -\frac{2}{\sqrt{1-{{\left( 2x-4 \right)}^{2}}}} \right]$

Multiplicando la parte del numerador, obtenemos:

$\displaystyle {y}'=-\frac{8{{\left[ \arccos \left( 2x-4 \right) \right]}^{3}}}{\sqrt{1-{{\left( 2x-4 \right)}^{2}}}}$

Que finalmente lo podemos dejar expresado de la siguiente manera:

Resultado:

$\displaystyle y'=-\frac{8{{\arccos }^{3}}\left( 2x-4 \right)}{\sqrt{1-{{\left( 2x-4 \right)}^{2}}}}$

Ejemplo 5. Resuelva la siguiente derivada

$\displaystyle y=\sqrt{arc\csc 6x}$

Solución:

Para este ejemplo podemos convertir a la función en su forma de potencia, de esta manera:

$\displaystyle y=\sqrt{arc\csc 6x}={{\left( arc\csc 6x \right)}^{\frac{1}{2}}}$

Ahora para poder derivar, verificamos que el argumento será u = arc csc 6x, y derivaremos como una potencia.

$\displaystyle y'=\frac{1}{2}{{\left( arc\csc 6x \right)}^{\frac{1}{2}-1}}\frac{d}{dx}\left( arc\csc 6x \right)$

Simplificando y aplicando la fórmula de derivación para un arco cosecante.

$\displaystyle y'=\frac{1}{2}{{\left( arc\csc 6x \right)}^{-\frac{1}{2}}}\left[ -\frac{\frac{d}{dx}\left( 6x \right)}{6x\sqrt{{{\left( 6x \right)}^{2}}-1}} \right]$

Resolviendo la derivada obtenemos:

$\displaystyle y'=\frac{1}{2}{{\left( arc\csc 6x \right)}^{-\frac{1}{2}}}\left[ -\frac{6}{6x\sqrt{{{\left( 6x \right)}^{2}}-1}} \right]$

Simplificando numerador y denominador

$\displaystyle y'=\frac{1}{2}{{\left( arc\csc 6x \right)}^{-\frac{1}{2}}}\left[ -\frac{1}{x\sqrt{{{\left( 6x \right)}^{2}}-1}} \right]$

Multiplicando y ordenando, para obtener el resultado final

Resultado:

$\displaystyle y'=-\frac{1}{2x\sqrt{arc\csc 6x}\sqrt{{{\left( 6x \right)}^{2}}-1}}$

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

3 Comentarios Publicados

Karla dice:

13 abril, 2020 a las 9:55 pm

Ayuda con una tarea

Responder
gloria aura juan perez dice:

23 octubre, 2020 a las 10:07 pm

alguien puede hacer favor de mandarme los dos de las derivada de funciones trigonometricas inversas, derivada de funciones exponenciales y logaritmicas

Responder
Marh dice:

18 abril, 2021 a las 5:20 pm

GX=✓✓✓✓cosx+sinx
Alguien

Responder

Deja una respuesta Cancelar la respuesta