Distancia de un punto a una recta - Ejercicios Resueltos

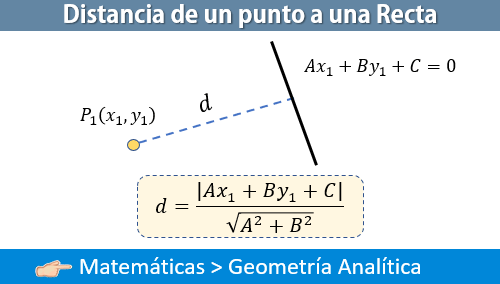
La distancia de un punto a una recta es un tema de gran importancia en geometría analítica, pues se puede hacer uso de este tema en temas de cálculo diferencial e integral, y física. Para ello vamos analizar su fórmula:

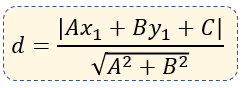
Formula de la distancia de un punto a una recta

La fórmula está definida para una gráfica similar a la de la imagen:

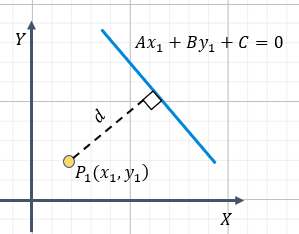
Como podemos observar, lo que se calcula es la longitud del segmento perpendicular a la recta trazado a partir del punto.

Veamos algunos ejemplos para entender mucho mejor este tema:

Ejemplos resueltos de la distancia de un punto a una Recta

Ejemplo 1. Encuentre la distancia del punto A (3,1) a la recta 6x -2y +11 = 0

Solución:

Para encontrar la distancia del punto A a la recta, solamente debemos sustituir nuestros datos en la fórmula, de la siguiente forma:

$\displaystyle d=\frac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

Sustituyendo las coordenadas del punto A y los coeficientes de la ecuación en la fórmula, vamos a obtener:

$\displaystyle d=\frac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\frac{\left| 6(3)-2(1)+11 \right|}{\sqrt{{{(6)}^{2}}+{{(-2)}^{2}}}}$

Multiplicando el numerador, obtenemos:

$\displaystyle d=\frac{\left| 27 \right|}{\sqrt{{{(6)}^{2}}+{{(-2)}^{2}}}}$

Ahora realizamos las operaciones en el denominador:

$\displaystyle d=\frac{\left| 27 \right|}{\sqrt{36+4}}=\frac{\left| 27 \right|}{\sqrt{40}}$

El valor absoluto de 27 es 27, entonces:

$\displaystyle d=\frac{\left| 27 \right|}{\sqrt{36+4}}=\frac{27}{\sqrt{40}}$

Por lo que el resultado, es:

Resultado:

$\displaystyle d=\frac{27}{\sqrt{40}}=4.269u$

Un aproximado a 4.269 unidades, de forma gráfica lo vemos así:

Distancia del Punto a una Recta

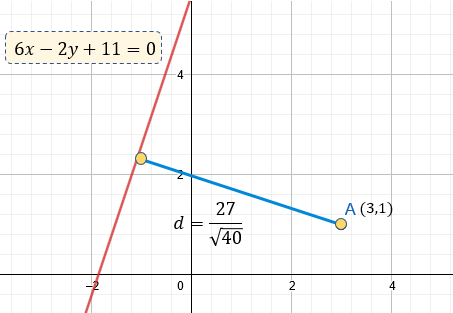
Veamos otro ejemplo.

Ejemplo 2. Determine la distancia de la recta 5x + 4y +15 = 0 al punto A (2, 3)

Solución:

Para obtener la distancia, debemos de aplicar nuestra fórmula y sustituir nuestros datos, de tal forma que:

$\displaystyle d=\frac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

Sustituyendo datos en la fórmula:

$\displaystyle d=\frac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\frac{\left| 5(2)+4(3)+15 \right|}{\sqrt{{{(5)}^{2}}+{{(4)}^{2}}}}$

Realizando las operaciones en el numerador, tenemos que:

$\displaystyle d=\frac{\left| 10+12+15 \right|}{\sqrt{{{(5)}^{2}}+{{(4)}^{2}}}}=\frac{\left| 37 \right|}{\sqrt{{{(5)}^{2}}+{{(4)}^{2}}}}$

Ahora realizamos las operaciones indicadas en el denominador:

$\displaystyle d=\frac{\left| 37 \right|}{\sqrt{25+16}}=\frac{\left| 37 \right|}{\sqrt{41}}$

El valor absoluto de 37 es 37.

$\displaystyle d=\frac{37}{\sqrt{41}}$

Por lo que el resultado es:

Resultado:

$\displaystyle d=\frac{37}{\sqrt{41}}=5.778u$

Que de forma gráfica, esto es:

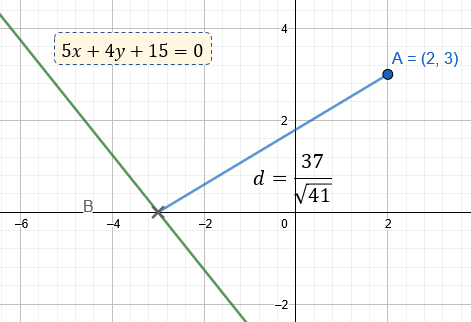
Veamos otro ejemplo más 😀

Ejemplo 3. Determine la distancia absoluta de la recta 2x + 5y +10 = 0 al punto A (1, 3)

Solución:

Nuevamente, para poder solucionar este problema que es similar a los dos anteriores. Veamos nuestra fórmula a utilizar:

$\displaystyle d=\frac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$

Vamos a sustituir nuestros datos en la fórmula:

$\displaystyle d=\frac{\left| A{{x}_{1}}+B{{y}_{1}}+C \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}}}=\frac{\left| 2(1)+5(3)+10 \right|}{\sqrt{{{(2)}^{2}}+{{(5)}^{2}}}}$

Vamos a realizar las operaciones en la parte del numerador y algunas del denominador:

$\displaystyle d=\frac{\left| 2+15+10 \right|}{\sqrt{4+25}}=\frac{\left| 27 \right|}{\sqrt{4+25}}$

Simplificamos aún más . . .

$\displaystyle d=\frac{\left| 27 \right|}{\sqrt{29}}$

El valor absoluto de 27 es 27, por lo que:

Resultado:

$\displaystyle d=\frac{27}{\sqrt{29}}=5.013u$

Qué sería la distancia del punto (1,3) a la recta dada. De forma gráfica esto se aprecia de la siguiente forma:

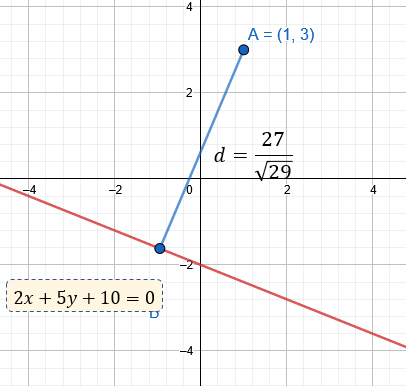
Distancia de un punto a una recta

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

8 Comentarios Publicados

Carlos Candelario dice:

5 septiembre, 2019 a las 9:02 pm

Excelente explicacion

Responder
ivan dice:

25 septiembre, 2019 a las 6:43 pm

Tres puntos de captación de agua están en A(-400,100), B(-300,300) y C(300,-300). Haciendo referencia a un punto base. Por BC pasa una tubería, Determine la longitud de tubería que se necesita para unir el punto A hacia la tubería que une BC. ¿O cuáles de los puntos debe unirse para emplear la menor cantidad de tubería?
alguien que me ayude

Responder
Mariany Cedeño dice:

19 junio, 2020 a las 3:31 pm

Deseó saber cuál es la distancia del punto (2,3) a la recta x-3y+2=0

Responder
1. Jennifer dice:
  
  30 octubre, 2021 a las 1:22 am
  
  La distancia es de 1.582 unidades.
  
  Responder
2. xim dice:
  
  18 noviembre, 2021 a las 2:04 pm
  
  1.581 u
  
  Responder
3. Diego Ruiz dice:
  
  3 abril, 2023 a las 12:00 am
  
  Para encontrar la distancia del punto (2,3) a la recta x - 3y + 2 = 0, se puede usar la fórmula de la distancia de un punto a una recta.
  La fórmula de la distancia de un punto (x1, y1) a una recta ax + by + c = 0 es:
  d = |ax1 + by1 + c| / √(a^2 + b^2)
  Para la recta x - 3y + 2 = 0, se tiene que a = 1, b = -3 y c = 2. Y para el punto (2,3), se tiene que x1 = 2 e y1 = 3.
  Reemplazando en la fórmula, se obtiene:
  d = |1(2) - 3(3) + 2| / √(1^2 + (-3)^2)
  d = |-5| / √(10)
  d = 5 / √10
  
  Responder
  1. elí benites dice:
    
    14 abril, 2024 a las 4:38 pm
    
    respuesta: 1.581
    
    Responder
Hernan dice:

7 junio, 2021 a las 12:31 pm

¡Como conocer un punto p=(x,y), teniendo como dato la recta L y la distancia del punto p a L.?

Responder

Deja una respuesta Cancelar la respuesta