20 Ejercicios Resueltos de Ley de Ohm en PDF
¿Alguna vez te has preguntado por qué tu cargador se calienta o cómo se calcula la batería que necesita un juguete? Todo se resume en la Ley de Ohm. Es el pilar fundamental de la electrónica y hoy no solo la entenderás, sino que aprenderás a resolver cualquier problema que te pongan en el examen.
¿Qué aprenderás en esta guía?
Dominarás:
- El famoso Triángulo de Ohm para despejar fórmulas.
- Cómo calcular Voltaje (V), Corriente (I) y Resistencia (R) por separado.
- Resolución de Circuitos Eléctricos simples.
- Acceso a nuestra Guía PDF con 20 Ejercicios.
- ¿Qué es la Ley de Ohm? (Fórmula y Concepto)
- ✅ Ejercicios Resueltos: Cálculo de Corriente (Intensidad)
- ✅ Ejercicios Resueltos: Cálculo de Voltaje (Tensión)
- ✅ Ejercicios Resueltos: Cálculo de Resistencia (R)
- ✅ Ejercicios de Circuitos Eléctricos (Ley de Ohm)
- Ejercicios Para Practicar (Ponte a Prueba)
- Descargar Guía: 20 Ejercicios de Ley de Ohm [PDF]
- Conclusión y Datos Históricos
¿Qué es la Ley de Ohm? (Fórmula y Concepto)
El físico George Simon Ohm descubrió que en los metales existe una relación mágica: la corriente que fluye es directamente proporcional al voltaje aplicado e inversamente proporcional a la resistencia.
La fórmula maestra es:
\[ I = \frac{V}{R} \]
Donde:
- I = Intensidad de Corriente [Amperes, A]
- V = Voltaje o Tensión [Volts, V]
- R = Resistencia Eléctrica [Ohms, \(\Omega\)]
Gráfica de Voltaje (V) vs Corriente (I)
Si graficamos el voltaje frente a la corriente en un material óhmico, obtenemos una línea recta que pasa por el origen. La pendiente de esta recta representa el valor de la resistencia ($R$).
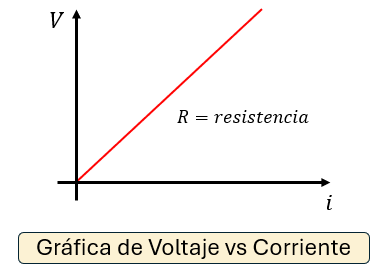
Nota: Si la gráfica no es recta, el material es "no óhmico" (como un diodo o un foco incandescente caliente).
El Triángulo de la Ley de Ohm (Truco para Memorizar)
Esta es la herramienta visual más buscada por los estudiantes. Tapa con tu dedo la letra que quieres calcular y verás la operación que debes hacer.
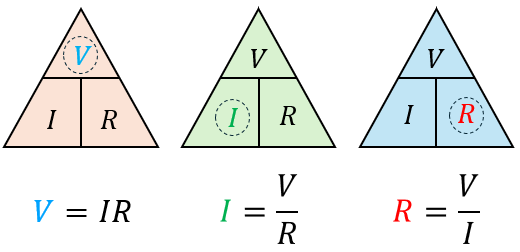
- Si buscas Voltaje (V): Tapa la V \(\rightarrow\) Queda \( I \cdot R \)
- Si buscas Corriente (I): Tapa la I \(\rightarrow\) Queda \( V / R \)
- Si buscas Resistencia (R): Tapa la R \(\rightarrow\) Queda \( V / I \)
✅ Ejercicios Resueltos: Cálculo de Corriente (Intensidad)
Empecemos calculando la "I". Recuerda la fórmula: \( I = V/R \).
Ejemplo 1: Lavadora de Juguete
Calcula la intensidad de la corriente que alimenta a una lavadora de juguete que tiene una resistencia de 10 ohmios y funciona con una batería con una diferencia de potencial de 30 V.
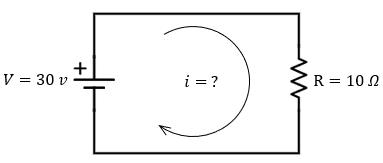
Solución:
Datos: \( R=10\Omega \), \( V=30V \).
\[ I=\frac{V}{R}=\frac{30V}{10\Omega }=3A \]
Resultado: 3 Amperes.
Ejemplo 2: Electrodoméstico
En un electrodoméstico con una resistencia de 12 \(\Omega\), se aplica un voltaje de 24 V. ¿Qué cantidad de corriente fluye por el conductor?
Solución:
\[ I=\frac{V}{R} = \frac{24V}{12\Omega} = 2A \]
Resultado: 2 Amperes.
Ejemplo 3: Conductor de 50 Ohms
¿Cuál es la intensidad de la corriente que circula por un conductor de 50 \(\Omega\) de resistencia, cuando en sus extremos se aplica una diferencia de potencial de 120 volts?
Solución:
\[ I=\frac{120V}{50\Omega }=2.4A \]
Resultado: 2.4 Amperes.
Ejemplo 4: Cargador de Celular
Un cargador de celular entrega 5 Volts a una resistencia interna de 2.5 \(\Omega\). ¿Cuánta corriente fluye hacia la batería?
Solución:
\[ I = \frac{V}{R} = \frac{5V}{2.5\Omega} = 2A \]
Resultado: 2 Amperes.
Ejemplo 5: Circuito de Alta Resistencia
Se aplica un voltaje de 100 V a un circuito con una resistencia de 2000 \(\Omega\) (2 \(k\Omega\)). Calcule la intensidad.
Solución:
\[ I = \frac{100V}{2000\Omega} = 0.05A \]
Resultado: 0.05 Amperes (o 50 mA).
✅ Ejercicios Resueltos: Cálculo de Voltaje (Tensión)
Aquí despejamos la V. La fórmula es: \( V = I \cdot R \).
Ejemplo 6: Circuito de Plancha
Calcula el voltaje, entre dos puntos del circuito de una plancha, por el que atraviesa una corriente de 4 amperios y presenta una resistencia de 10 ohmios.
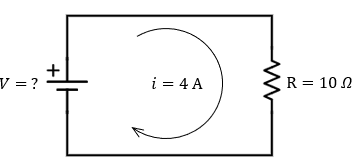
Solución:
Datos:
\( I=4A \), \( R=10\Omega \).
\[ V = I \cdot R = (4A)(10\Omega) = 40V \]
Resultado: 40 Volts.
Ejemplo 7: Circuito Básico
Un circuito eléctrico tiene una resistencia de 5 \(\Omega\) y una corriente de 2 A fluyendo a través de él. ¿Cuál es el voltaje del circuito?
Solución:
\[ V = (2A)(5\Omega) = 10V \]
Resultado: 10 Volts.
Ejemplo 8: Corriente Alta
Una intensidad de corriente de 6.5 A circula por un conductor de 27 \(\Omega\). ¿Cuál es la diferencia de potencial (Voltaje)?
Solución:
\[ V = (6.5A)(27\Omega) = 175.5V \]
Resultado: 175.5 Volts.
Ejemplo 9: Caída de Tensión
Por una resistencia de 8 \(\Omega\) pasa una corriente de 1.5 A. ¿Cuál es la caída de tensión (voltaje) en dicha resistencia?
Solución:
\[ V = I \cdot R = (1.5A)(8\Omega) = 12V \]
Resultado: 12 Volts.
Ejemplo 10: Batería de Auto
Al arrancar un auto, el motor de arranque consume 150 A y tiene una resistencia de 0.08 \(\Omega\). ¿Qué voltaje suministra la batería?
Solución:
\[ V = (150A)(0.08\Omega) = 12V \]
Resultado: 12 Volts.
✅ Ejercicios Resueltos: Cálculo de Resistencia (R)
Despejamos la R. La fórmula es: \( R = V/I \).
Ejemplo 11: Calculando la Resistencia
Calcula la resistencia atravesada por una corriente con una intensidad de 5 amperios y una diferencia de potencial de 11 voltios.
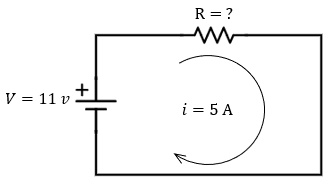
Solución:
Datos: \( I=5A \), \( V=11V \).
\[ R = \frac{V}{I} = \frac{11V}{5A} = 2.2\Omega \]
Resultado: 2.2 Ohms.
Ejemplo 12: Fuente de 15V
Un circuito está conectado a una fuente de 15 V y permite el paso de una corriente de 3 A. ¿Cuál es la resistencia del circuito?
Solución:
\[ R = \frac{15V}{3A} = 5\Omega \]
Resultado: 5 Ohms.
Ejemplo 13: Resistencia de una Estufa
Una estufa eléctrica se conecta a 220 V y consume una corriente de 11 A. ¿Cuál es el valor de su resistencia interna?
Solución:
\[ R = \frac{V}{I} = \frac{220V}{11A} = 20\Omega \]
Resultado: 20 Ohms.
Ejemplo 14: Bocina (Parlante)
Un amplificador entrega 24 V a una bocina y hace circular 3 A. ¿De cuántos Ohms es la impedancia (resistencia) de la bocina?
Solución:
\[ R = \frac{24V}{3A} = 8\Omega \]
Resultado: 8 Ohms.
✅ Ejercicios de Circuitos Eléctricos (Ley de Ohm)
A veces no te dan los datos directos, sino un diagrama. Aquí es donde debes saber leer circuitos.
Ejemplo 15: Circuito con Resistencias en Paralelo
¿Cuál es la corriente total que pasa a través de la batería en el siguiente circuito eléctrico?
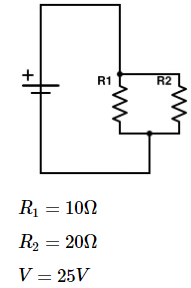
Solución:
Para encontrar la corriente total, primero debemos reducir el circuito a una sola Resistencia Equivalente ($R_T$).
Paso 1: Sumar resistencias en Paralelo
Recordamos la fórmula para dos resistencias en paralelo:
\[ \frac{1}{R_T} = \frac{1}{R_1} + \frac{1}{R_2} \]
Sustituimos los valores ($10\Omega$ y $20\Omega$):
\[ \frac{1}{R_T} = \frac{1}{10} + \frac{1}{20} \]
Hacemos la suma de fracciones (común denominador 20):
\[ \frac{1}{R_T} = \frac{2}{20} + \frac{1}{20} = \frac{3}{20} \]
Invertimos la fracción para obtener $R_T$:
\[ R_T = \frac{20}{3} = 6.66 \Omega \]
Paso 2: Calcular la Intensidad Total
Ahora que tenemos la resistencia total y el voltaje total (25V), aplicamos la Ley de Ohm:
\[ I = \frac{V}{R_T} = \frac{25V}{6.66\Omega} = 3.75 A \]
Resultado: La corriente total es de 3.75 Amperes.
Ejemplo 16: Circuito Mixto (Reto)
Dado el siguiente circuito, encuentre la corriente a través de la resistencia "R3".
Datos: \(V_{total}=4.5V\), \(R_1=3\Omega\), \(R_2=6\Omega\), \(R_3=3\Omega\), \(R_4=3\Omega\).
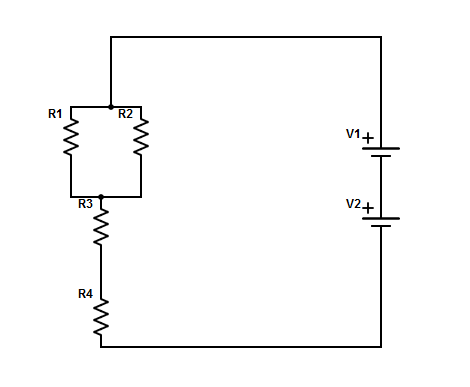
Solución:
Este es un circuito mixto. Para hallar la corriente en $R_3$, necesitamos reducir el circuito desde la derecha hacia la izquierda para encontrar la corriente total y luego ver cómo se divide.
Paso 1: Reducir la Serie ($R_3$ y $R_4$)
Las resistencias $R_3$ y $R_4$ están en la misma rama (una tras otra), por lo tanto están en serie.
\[ R_{3-4} = R_3 + R_4 = 3\Omega + 3\Omega = 6\Omega \]
Paso 2: Reducir el Paralelo ($R_2$ y $R_{3-4}$)
Ahora, la resistencia $R_2$ está en paralelo con la suma que acabamos de calcular ($R_{3-4}$).
\[ R_{paralelo} = \frac{R_2 \cdot R_{3-4}}{R_2 + R_{3-4}} = \frac{6 \cdot 6}{6 + 6} = \frac{36}{12} = 3\Omega \]
Paso 3: Resistencia Total del Circuito
Finalmente, nos queda la resistencia $R_1$ en serie con el bloque paralelo que calculamos.
\[ R_{Total} = R_1 + R_{paralelo} = 3\Omega + 3\Omega = 6\Omega \]
Paso 4: Calcular Corriente Total ($I_T$)
\[ I_{Total} = \frac{V_{Total}}{R_{Total}} = \frac{4.5V}{6\Omega} = 0.75 A \]
Paso 5: Calcular la corriente en R3
La corriente total de $0.75 A$ sale de la fuente y pasa por $R_1$. Al llegar al nodo, se divide en dos caminos:
1. Camino A: Pasa por $R_2$ ($6\Omega$).
2. Camino B: Pasa por la rama de $R_3+R_4$ (que también suma $6\Omega$).
Como ambas ramas tienen la misma resistencia ($6\Omega$), la corriente se divide exactamente a la mitad:
\[ I_{R3} = \frac{I_{Total}}{2} = \frac{0.75 A}{2} = 0.375 A \]
Resultado: La corriente que pasa por la resistencia R3 es de 0.375 Amperes (o 375 mA).
Ejercicios Para Practicar (Ponte a Prueba)
Intenta resolverlos mentalmente o en tu cuaderno antes de ver la solución.
Problema 17: El Tostador
Un tostador eléctrico posee una resistencia de 40 \(\Omega\) cuando está caliente. ¿Cuál será la intensidad de la corriente al conectarlo a una línea de 120 V?
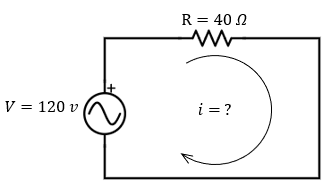
▶︎ Haz clic aquí para ver la solución
\( I = 120V / 40\Omega = 3 \text{ Amperes} \)
Problema 18: Resistencia Desconocida
Determina el valor de la resistencia de un circuito de 110 V por el que pasa una corriente de 3 A.
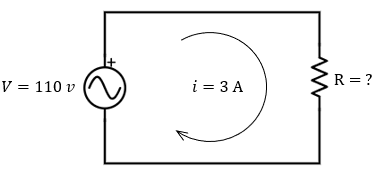
▶︎ Haz clic aquí para ver la solución
\( R = 110V / 3A = 36.66 \Omega \)
Problema 19: Diferencia de Potencial
Calcular el voltaje en una resistencia de 25 \(\Omega\) si por ella fluyen 8 A.
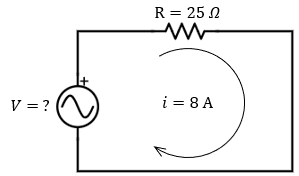
▶︎ Haz clic aquí para ver la solución
\( V = 8A \times 25\Omega = 200 \text{ Volts} \)
Problema 20: Divisor de Voltaje
Dado el siguiente circuito, con voltaje de entrada de 12 V y corriente de 2 A. Si el voltaje medido entre R1 y tierra es de 8V, ¿cuál es el valor de R1?
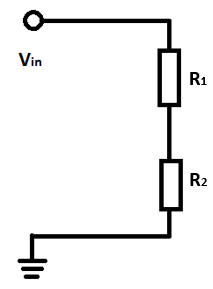
▶︎ Haz clic aquí para ver la solución
Si el voltaje en R1 es 4V (12-8) y la corriente es 2A:
\( R1 = 4V / 2A = 2 \Omega \)
Problema 21: Corriente en Serie
Si cada resistencia en el diagrama tiene un valor de 2 \(\Omega\), ¿cuánta corriente fluye a través del circuito?
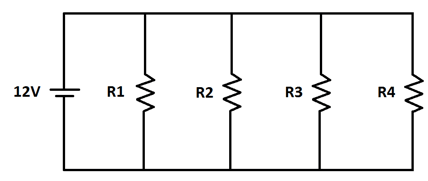
▶︎ Haz clic aquí para ver la solución
Asumiendo un voltaje dado en la imagen o estándar. Si es serie, \(R_T = 2+2+2 = 6\Omega\). La corriente sería \(V/6\).
Descargar Guía: 20 Ejercicios de Ley de Ohm [PDF]
¿Quieres aprobar tu examen sí o sí? Hemos recopilado 20 ejercicios (resueltos y propuestos) que cubren desde lo básico hasta circuitos complejos de Kirchhoff.
🔒 Incluye Circuitos Serie, Paralelo y Mixtos • 100% Gratis
Conclusión y Datos Históricos
La Ley de Ohm es solo el comienzo. A medida que avances, te encontrarás con componentes que no siguen esta ley (no óhmicos), pero para el 90% de la electrónica básica, esta fórmula es tu mejor amiga.
💡 Sobre George Simon Ohm
George Simon Ohm (1789-1854), físico alemán, fue quien descubrió esta relación. Curiosamente, en su época fue criticado y su trabajo ignorado, pero hoy la unidad de resistencia (Ohm, \(\Omega\)) lleva su nombre en su honor.
Aplicaciones Reales
- Diseño de cargadores de celular.
- Cálculo de fusibles para protección de casas.
- Control de brillo en pantallas y LEDs.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Muy útil !!!
★★★★★
-
Excelente material de estudio, muchas gracias.
★★★★★
-
Me gusto sta materia es super buena
★★★★★
-
herramienta util, gracias
★★★★★
-
Muy interesante.
★★★★★
196 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar