Regla de los 4 Pasos para Derivar: 20 Ejercicios Resueltos [PDF]
Si estás empezando con el Cálculo Diferencial, seguro tu profesor te ha pedido derivar "por definición" o usando la famosa Regla de los 4 Pasos. Al principio parece un método largo y tedioso (¡y lo es!), pero es fundamental para entender de dónde salen todas las fórmulas mágicas de derivación.
En este artículo no solo te explicaré el concepto; vamos a resolver 10 ejercicios paso a paso (desde los fáciles hasta raíces y fracciones) para que apruebes tu examen con los ojos cerrados.
¿Qué aprenderás hoy?
En esta guía dominarás:
- El significado geométrico de la derivada (Secante a Tangente).
- Los 4 Pasos detallados (Incrementar, Restar, Dividir, Límite).
- 20 Ejercicios Resueltos de polinomios, fracciones y raíces.
- Acceso a nuestro PDF con ejercicios extra.
¿Qué es la Regla de los 4 Pasos?
La derivada no es más que un límite. Matemáticamente se define como:
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
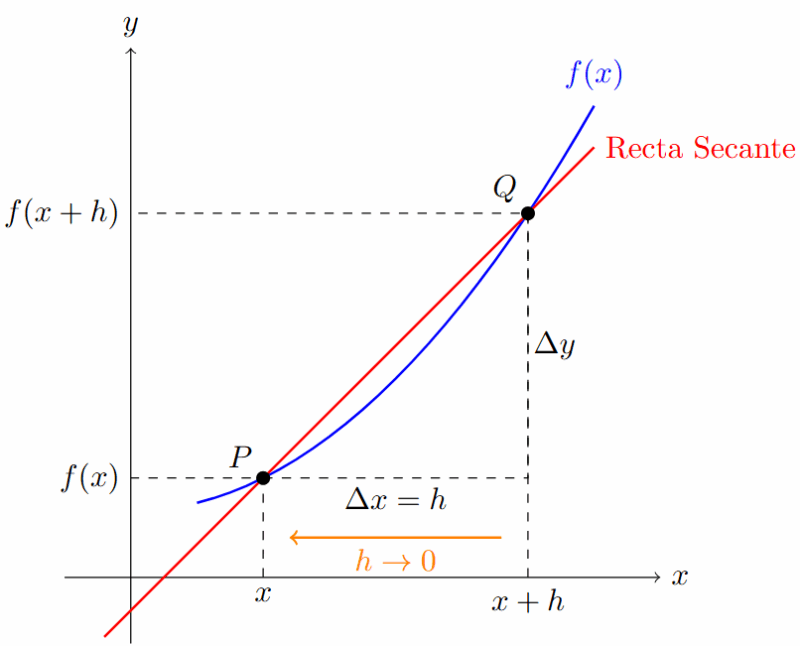
A veces verás que usan $\Delta x$ en lugar de $h$. Es exactamente lo mismo: un incremento muy pequeño en el eje X.
La regla de los 4 pasos es simplemente un método ordenado para resolver este límite sin perderte en el álgebra.
Los 4 Pasos Desglosados
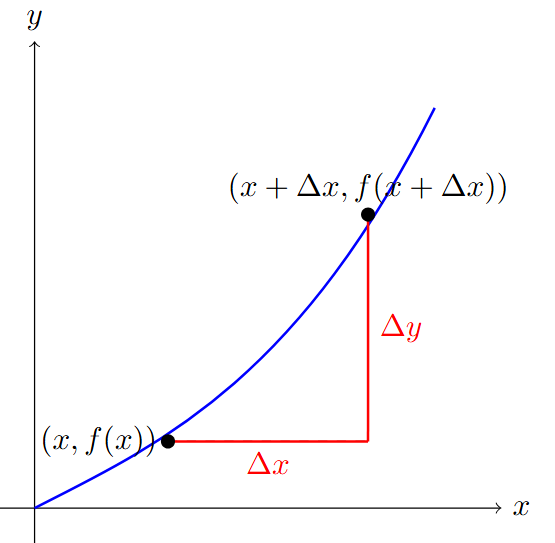
- Paso 1 (Incrementar): Sustituye cada \( x \) en la función por \( (x + h) \) o \( (x + \Delta x) \).
- Paso 2 (Restar): A la función incrementada, réstale la función original \( f(x) \). Simplifica los términos que se puedan.
- Paso 3 (Dividir): Divide todo el resultado entre \( h \) (o \( \Delta x \)). Factoriza si es necesario para eliminar la \( h \) del denominador.
- Paso 4 (Límite): Calcula el límite cuando \( h \to 0 \). Esto te dará la derivada final \( f'(x) \).
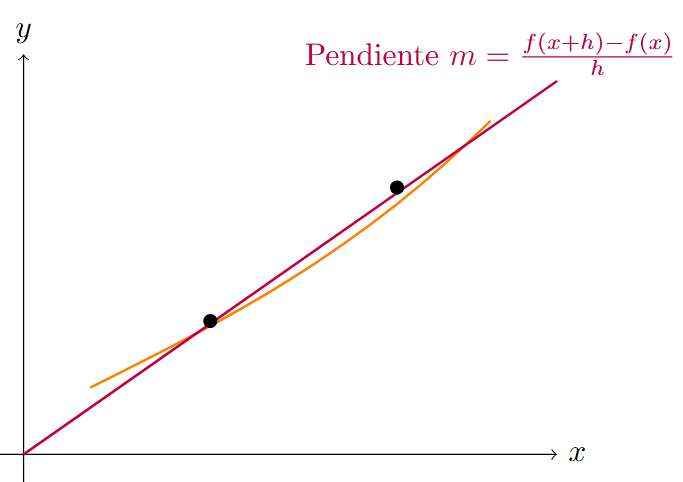
✅ 10 Ejercicios Resueltos por la Regla de los 4 Pasos
Vamos a subir la dificultad gradualmente. Empezaremos con funciones lineales y cuadráticas, y terminaremos con racionales y radicales.
Nivel 1: Funciones Polinómicas (Básicas)
Ejemplo 1: Función Cuadrática
Deriva la función \( y = 5x^2 \) usando la regla de los 4 pasos.
Solución:
Paso 1 (Incrementar): Sustituimos \(x\) por \((x+h)\):
\[ f(x+h) = 5(x+h)^2 = 5(x^2 + 2xh + h^2) = 5x^2 + 10xh + 5h^2 \]
Paso 2 (Restar): Restamos la función original \(5x^2\):
\[ f(x+h) - f(x) = (5x^2 + 10xh + 5h^2) - 5x^2 \]
\[ = 10xh + 5h^2 \]
Paso 3 (Dividir): Dividimos entre \(h\):
\[ \frac{10xh + 5h^2}{h} = \frac{h(10x + 5h)}{h} = 10x + 5h \]
Paso 4 (Límite): Hacemos \(h \to 0\):
\[ \lim_{h \to 0} (10x + 5h) = 10x + 5(0) = 10x \]
Resultado: \( f'(x) = 10x \)
Ejemplo 2: Función Cúbica
Encuentra la derivada de \( y = x^3 + 2 \).
Solución:
Paso 1:
\[ f(x+h) = (x+h)^3 + 2 = (x^3 + 3x^2h + 3xh^2 + h^3) + 2 \]
Paso 2:
\[ f(x+h) - f(x) = (x^3 + 3x^2h + 3xh^2 + h^3 + 2) - (x^3 + 2) \]
Se cancelan \(x^3\) y \(2\):
\[ = 3x^2h + 3xh^2 + h^3 \]
Paso 3:
\[ \frac{3x^2h + 3xh^2 + h^3}{h} = \frac{h(3x^2 + 3xh + h^2)}{h} = 3x^2 + 3xh + h^2 \]
Paso 4:
\[ \lim_{h \to 0} (3x^2 + 3xh + h^2) = 3x^2 + 0 + 0 = 3x^2 \]
Resultado: \( f'(x) = 3x^2 \)
Ejemplo 3: Polinomio Completo
Deriva \( f(x) = 3x^2 - 5x + 1 \).
Solución:
Paso 1:
\[ f(x+h) = 3(x+h)^2 - 5(x+h) + 1 \]
\[ = 3(x^2 + 2xh + h^2) - 5x - 5h + 1 \]
\[ = 3x^2 + 6xh + 3h^2 - 5x - 5h + 1 \]
Paso 2 (Restar Original):
Restamos \( (3x^2 - 5x + 1) \). Se eliminan los términos sin \(h\):
\[ = 6xh + 3h^2 - 5h \]
Paso 3 (Dividir):
\[ \frac{h(6x + 3h - 5)}{h} = 6x + 3h - 5 \]
Paso 4 (Límite):
\[ \lim_{h \to 0} (6x + 3h - 5) = 6x - 5 \]
Resultado: \( f'(x) = 6x - 5 \)
Nivel 2: Funciones Racionales (Fracciones)
Aquí el álgebra se pone interesante. Necesitarás sumar fracciones algebraicas.
Ejemplo 4: Fracción Simple
Deriva \( y = \frac{1}{x} \).
Solución:
Paso 1: \( f(x+h) = \frac{1}{x+h} \)
Paso 2: Restamos \( \frac{1}{x} \):
\[ \frac{1}{x+h} - \frac{1}{x} = \frac{x - (x+h)}{x(x+h)} = \frac{x - x - h}{x(x+h)} = \frac{-h}{x(x+h)} \]
Paso 3: Dividimos entre \(h\) (multiplicamos denominador por \(h\)):
\[ \frac{-h}{h \cdot x(x+h)} = \frac{-1}{x(x+h)} \]
Paso 4: Límite \(h \to 0\):
\[ \lim_{h \to 0} \frac{-1}{x(x+0)} = \frac{-1}{x^2} \]
Resultado: \( f'(x) = -\frac{1}{x^2} \)
Ejemplo 5: Racional Lineal
Deriva \( y = \frac{3x+2}{2x-1} \).
Solución:
Paso 1:
\[ f(x+h) = \frac{3(x+h)+2}{2(x+h)-1} = \frac{3x+3h+2}{2x+2h-1} \]
Paso 2 (Resta de Fracciones):
\[ \frac{3x+3h+2}{2x+2h-1} - \frac{3x+2}{2x-1} \]
Multiplicamos cruzado (denominador común):
Num: \( (3x+3h+2)(2x-1) - (3x+2)(2x+2h-1) \)
Al desarrollar y simplificar el numerador (hazlo con calma), notarás que se cancelan casi todos los términos, quedando solo: \( -7h \).
Paso 3:
\[ \frac{-7h}{h(2x+2h-1)(2x-1)} = \frac{-7}{(2x+2h-1)(2x-1)} \]
Paso 4:
\[ \lim_{h \to 0} \frac{-7}{(2x-1)(2x-1)} = \frac{-7}{(2x-1)^2} \]
Resultado: \( f'(x) = \frac{-7}{(2x-1)^2} \)
Ejemplo 6: Inversa Cuadrática
Deriva \( f(x) = \frac{2}{x^2} \).
Solución:
Paso 1: \( \frac{2}{(x+h)^2} \)
Paso 2:
\[ \frac{2}{(x+h)^2} - \frac{2}{x^2} = \frac{2x^2 - 2(x+h)^2}{x^2(x+h)^2} = \frac{2x^2 - 2(x^2+2xh+h^2)}{...} \]
\[ = \frac{-4xh - 2h^2}{x^2(x+h)^2} \]
Paso 3: Dividir entre \(h\):
\[ \frac{h(-4x - 2h)}{h \cdot x^2(x+h)^2} = \frac{-4x - 2h}{x^2(x+h)^2} \]
Paso 4: Límite \(h \to 0\):
\[ \frac{-4x}{x^2(x^2)} = \frac{-4x}{x^4} = -\frac{4}{x^3} \]
Resultado: \( f'(x) = -4x^{-3} \)
Nivel 3: Funciones con Raíces (Radicales)
Para estos ejercicios, el truco es racionalizar (multiplicar por el conjugado).
Ejemplo 7: Raíz Cuadrada Simple
Deriva \( y = \sqrt{x} \).
Solución:
Paso 1: \( \sqrt{x+h} \)
Paso 2: \( \sqrt{x+h} - \sqrt{x} \)
Multiplicamos por el conjugado \( \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}} \):
\[ = \frac{(x+h) - x}{\sqrt{x+h} + \sqrt{x}} = \frac{h}{\sqrt{x+h} + \sqrt{x}} \]
Paso 3: Dividir entre \(h\):
\[ \frac{h}{h(\sqrt{x+h} + \sqrt{x})} = \frac{1}{\sqrt{x+h} + \sqrt{x}} \]
Paso 4: Límite \(h \to 0\):
\[ \frac{1}{\sqrt{x} + \sqrt{x}} = \frac{1}{2\sqrt{x}} \]
Resultado: \( f'(x) = \frac{1}{2\sqrt{x}} \)
Ejemplo 8: Raíz con Suma
Deriva \( y = \sqrt{x+5} \).
Solución:
Similar al anterior.
Numerador tras restar y racionalizar:
\[ (x+h+5) - (x+5) = h \]
Denominador:
\( h(\sqrt{x+h+5} + \sqrt{x+5}) \)
Al cancelar \(h\) y aplicar límite:
\[ \frac{1}{\sqrt{x+5} + \sqrt{x+5}} = \frac{1}{2\sqrt{x+5}} \]
Resultado:
\( f'(x) = \frac{1}{2\sqrt{x+5}} \)
Ejemplo 9: Raíz Inversa
Deriva \( f(x) = \frac{1}{\sqrt{x}} \).
Solución:
Este es para expertos. Combina fracciones y raíces.
Resta: \( \frac{1}{\sqrt{x+h}} - \frac{1}{\sqrt{x}} = \frac{\sqrt{x} - \sqrt{x+h}}{\sqrt{x+h}\sqrt{x}} \)
Racionalizando el numerador:
\[ \frac{x - (x+h)}{\sqrt{x+h}\sqrt{x}(\sqrt{x} + \sqrt{x+h})} = \frac{-h}{...} \]
Dividiendo entre \(h\) y aplicando límite:
\[ \frac{-1}{\sqrt{x}\sqrt{x}(2\sqrt{x})} = \frac{-1}{x(2\sqrt{x})} = -\frac{1}{2x^{3/2}} \]
Resultado: \( f'(x) = -\frac{1}{2x\sqrt{x}} \)
Ejemplo 10: Polinomio de Grado 4
Deriva \( y = x^4 \).
Solución:
Necesitas el Binomio de Newton o Triángulo de Pascal (1, 4, 6, 4, 1).
Paso 1: \( (x+h)^4 = x^4 + 4x^3h + 6x^2h^2 + 4xh^3 + h^4 \)
Paso 2: Restar \(x^4\). Queda \( 4x^3h + 6x^2h^2 + 4xh^3 + h^4 \)
Paso 3: Dividir entre \(h\). Queda \( 4x^3 + 6x^2h + 4xh^2 + h^3 \)
Paso 4: Límite \(h \to 0\). Todos los términos con \(h\) desaparecen.
Queda solo \( 4x^3 \).
Resultado: \( f'(x) = 4x^3 \)
🔥 Ejercicios Avanzados (Trigonometría y Racionales)
Si llegaste hasta aquí, ya dominas lo básico. Ahora veremos cómo aplicar la regla de los 4 pasos a funciones que requieren identidades trigonométricas y álgebra avanzada.
Ejemplo 11: Polinomio Mixto
Deriva \( y = x^2 - 4x \).
Solución:
Paso 1: \( (x+h)^2 - 4(x+h) = x^2 + 2xh + h^2 - 4x - 4h \)
Paso 2 (Restar): \( (x^2 + 2xh + h^2 - 4x - 4h) - (x^2 - 4x) = 2xh + h^2 - 4h \)
Paso 3 (Dividir): \( \frac{h(2x + h - 4)}{h} = 2x + h - 4 \)
Paso 4 (Límite): \( 2x + 0 - 4 \)
Resultado: \( f'(x) = 2x - 4 \)
Ejemplo 12: Binomio al Cubo
Deriva \( y = (x-1)^3 \).
Solución:
Desarrollamos primero la función: \( y = x^3 - 3x^2 + 3x - 1 \).
Al aplicar los 4 pasos (similar al ejemplo de \(x^3\)), los términos constantes y lineales se simplifican.
Resultado: \( f'(x) = 3(x-1)^2 \) o \( 3x^2 - 6x + 3 \)
Ejemplo 13: Fracción con Binomio
Deriva \( y = \frac{3}{x-2} \).
Solución:
Paso 1: \( \frac{3}{x+h-2} \)
Paso 2: \( \frac{3}{x+h-2} - \frac{3}{x-2} = \frac{3(x-2) - 3(x+h-2)}{(x+h-2)(x-2)} = \frac{-3h}{...} \)
Paso 3: \( \frac{-3}{(x+h-2)(x-2)} \)
Paso 4: \( h \to 0 \Rightarrow \frac{-3}{(x-2)(x-2)} \)
Resultado: \( f'(x) = \frac{-3}{(x-2)^2} \)
Ejemplo 14: Racional Clásica
Deriva \( f(x) = \frac{x}{x+1} \).
Solución:
Paso 2 (Resta): \( \frac{x+h}{x+h+1} - \frac{x}{x+1} \)
Num: \( (x+h)(x+1) - x(x+h+1) = (x^2+x+hx+h) - (x^2+xh+x) = h \)
Paso 3: \( \frac{h}{h(x+h+1)(x+1)} = \frac{1}{(x+h+1)(x+1)} \)
Resultado: \( f'(x) = \frac{1}{(x+1)^2} \)
Ejemplo 15: Racional Cuadrática
Deriva \( y = \frac{1}{x^2+1} \).
Solución:
Al restar y simplificar el numerador nos queda: \( -2xh - h^2 \).
Al dividir entre \(h\) y aplicar límite:
Resultado: \( f'(x) = \frac{-2x}{(x^2+1)^2} \)
Ejemplo 16: Raíz con Coeficiente
Deriva \( y = \sqrt{3x} \).
Solución:
Racionalizando con conjugado \( \sqrt{3(x+h)} + \sqrt{3x} \):
Numerador queda \( 3(x+h) - 3x = 3h \).
Resultado: \( f'(x) = \frac{3}{2\sqrt{3x}} \)
Ejemplo 17: Raíz en Denominador Compleja
Deriva \( y = \frac{1}{\sqrt{x+1}} \).
Solución:
Combinación de fracciones y racionalización.
Resultado: \( f'(x) = -\frac{1}{2(x+1)^{3/2}} \)
Derivadas Trigonométricas por Definición
Aquí usamos la identidad clave: \( \lim_{h \to 0} \frac{\sin h}{h} = 1 \) y \( \lim_{h \to 0} \frac{\cos h - 1}{h} = 0 \).
Ejemplo 18: Seno de x
Deriva \( f(x) = \sin(x) \).
Solución:
Paso 1: \( \sin(x+h) = \sin x \cos h + \cos x \sin h \)
Paso 2: \( \sin x \cos h + \cos x \sin h - \sin x \)
Agrupamos: \( \sin x (\cos h - 1) + \cos x \sin h \)
Paso 3: \( \sin x \frac{\cos h - 1}{h} + \cos x \frac{\sin h}{h} \)
Paso 4: Aplicamos límites especiales (0 y 1).
\( \sin x (0) + \cos x (1) \)
Resultado: \( f'(x) = \cos(x) \)
Ejemplo 19: Coseno de x
Deriva \( f(x) = \cos(x) \).
Solución:
Usamos \( \cos(x+h) = \cos x \cos h - \sin x \sin h \).
Siguiendo el proceso análogo al seno:
Resultado: \( f'(x) = -\sin(x) \)
Ejemplo 20: Función Constante
Deriva \( f(x) = 5 \).
Solución:
Parece trampa, pero es importante.
Paso 1: \( f(x+h) = 5 \) (No hay x donde sustituir)
Paso 2: \( 5 - 5 = 0 \)
Paso 3: \( 0/h = 0 \)
Resultado: \( f'(x) = 0 \)
Descargar PDF de Regla de los 4 Pasos
Si necesitas más ejercicios para practicar antes del examen, descarga nuestra guía completa.
🔒 Descarga segura desde Google Drive • 100% Gratuito
Conclusión
Puntos Clave
La regla de los 4 pasos es la base del cálculo. Aunque en la práctica usarás fórmulas directas (como \( \frac{d}{dx} x^n = nx^{n-1} \)), entender este proceso te ayuda a comprender qué es una tasa de cambio instantánea.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Quiero ocupar
-
Ayúdenme con una derivada por favor
-
Y si la raiz esta elevada? Se hace igual o cambia algo?
-
Y=2x⁴-3x³+5x²-6x+3
-
Y=2x
76 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar