Conversión de Unidades: 50 Ejercicios Resueltos [PDF] + Guía
¿Alguna vez te has preguntado por qué es crucial dominar la conversión de unidades en física? No se trata solo de mover puntos decimales; es el lenguaje universal que permite a ingenieros y científicos de todo el mundo comunicarse sin errores catastróficos. Hoy no solo aprenderás teoría; te voy a guiar a través de una Guía Maestra con Ejercicios Resueltos que te convertirán en un experto transformando kilómetros a millas, horas a segundos y mucho más.
¿Qué aprenderás en esta guía?
En este artículo dominarás:
- Los sistemas de unidades históricos y el Sistema Internacional (SI).
- El método infalible del Factor de Conversión (matemáticamente correcto).
- Cómo convertir unidades compuestas (velocidad, densidad).
- Más de 30 ejercicios resueltos paso a paso.
- Acceso a nuestro PDF con 50 ejercicios de práctica. 🚀
- Historia y Sistemas de Unidades
- Magnitudes Derivadas y Compuestas
- El Método del Factor de Conversión (La Clave del Éxito)
- Ejercicios Resueltos de Conversión de Unidades (Paso a Paso)
- Más Ejercicios de Práctica (Variados)
- Problemas Propuestos para Practicar (¡Ponte a Prueba!)
- Descargar PDF con 50 Ejercicios Resueltos
Historia y Sistemas de Unidades
No se puede realizar una conversión de unidades correcta si no entendemos el origen. A lo largo de la historia, la humanidad ha necesitado estandarizar cómo medimos el mundo.
Sistema Métrico Decimal
Este sistema nació de una necesidad global. Fue creado en una convención mundial de ciencia celebrada en París, Francia, en el año 1795. Fue el primer patrón real que existió para medidas como el metro, el kilogramo-peso y el litro.
💡 ¡Curiosidad Histórica!
¿Sabías que para definir el metro original utilizaron la dimensión de la Tierra? Se dividió un meridiano de nuestro planeta en 40 millones de partes iguales, y a la longitud de una de esas partes se le llamó metro. ¡Así de grande es la física!
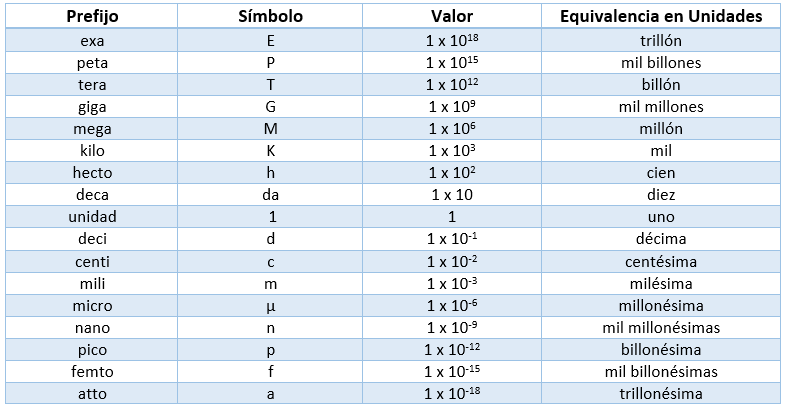
Una característica vital de este sistema es su división decimal, usando prefijos que seguramente conoces:
- Decímetro: décima parte del metro.
- Centímetro: centésima parte del metro.
- Milímetro: milésima parte del metro.
Sistema Cegesimal (CGS)
En el siglo XVIII, liderado por el genio matemático Karl Gauss, se propuso el sistema CGS (Centímetro - Gramo - Segundo). Fue muy usado en la física teórica clásica.
Sistema MKS y el Sistema Internacional (SI)
A principios del siglo XX, Giovanni Giorgi propuso el sistema MKS (Metro - Kilogramo - Segundo). Este fue el abuelo del actual Sistema Internacional de Unidades (SI), que es el estándar moderno usado en casi todo el mundo (excepto en países que usan el sistema inglés).
El SI establece 7 magnitudes fundamentales:
- Longitud → Metro (m)
- Masa → Kilogramo (kg)
- Tiempo → Segundo (s)
- Temperatura → Kelvin (K)
- Intensidad de Corriente → Ampere (A)
- Intensidad Luminosa → Candela (cd)
- Cantidad de Sustancia → Mol (mol)
Magnitudes Derivadas y Compuestas
Las magnitudes derivadas son aquellas que resultan de combinar las fundamentales. Aquí es donde muchos estudiantes fallan, pero tú no lo harás.
Por ejemplo, la velocidad es distancia sobre tiempo:
\[ v = \frac{m}{s} \]
Otras comunes son la aceleración ($m/s^2$), fuerza (Newton), presión (Pascal) y densidad ($kg/m^3$).

El Método del Factor de Conversión (La Clave del Éxito)
Antes de pasar a los ejercicios resueltos, debes entender la herramienta matemática más potente: El Factor de Conversión.
Muchos intentan usar la "Regla de Tres", pero en física avanzada, la regla de tres puede causar confusiones. El método del factor de conversión consiste en multiplicar tu cantidad original por una fracción que vale 1, donde el numerador y el denominador son equivalentes pero en diferentes unidades.
Regla de Oro: La unidad que quieres eliminar debe ir en el lado opuesto de la fracción para que se cancele matemáticamente.
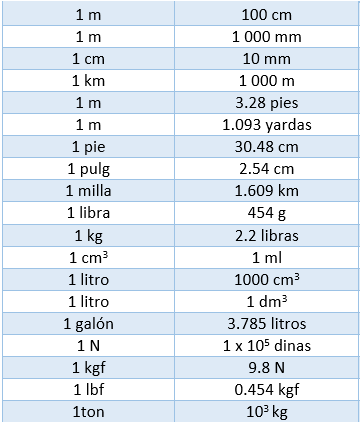
Tabla de Equivalencias Comunes
Ten esta tabla a la mano, la usarás para todos los ejercicios siguientes:
Ejercicios Resueltos de Conversión de Unidades (Paso a Paso)
Vamos a aplicar la teoría. Analiza detalladamente cómo cancelamos las unidades en cada paso.
Ejemplo 1: Conversión de Longitud (km a m)
Convierta 4 km a metros.
Solución:
Miramos la tabla: 1 km = 1000 m.
Aplicamos el factor de conversión colocando el kilómetro abajo para que se elimine con el de arriba:
\[ 4 \text{ km} \left( \frac{1000 \text{ m}}{1 \text{ km}} \right) = 4000 \text{ m} \]
Observa algo importante: siempre que se usa un factor de conversión, se intenta que las unidades queden cruzadas (una arriba y una abajo) para poder eliminarlas.
Visualmente, así se cancelan las unidades: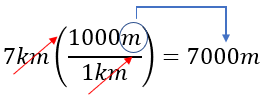
Ejemplo 2: Conversión Sistema Inglés (Pies a Metros)
Convierta 7 pies a metros.
Solución:
Factor de conversión: 1 metro = 3.28 pies (ft).
Colocamos "pies" abajo para cancelar:
\[ 7 \text{ pies} \left( \frac{1 \text{ m}}{3.28 \text{ pies}} \right) = 2.134 \text{ m} \]
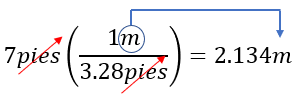
Ejercicios de Conversión de Unidades de Velocidad
Aquí entramos a las unidades compuestas. Muchos estudiantes buscan cómo convertir km/h a m/s. El truco es usar dos factores de conversión seguidos: uno para la longitud y otro para el tiempo.
Ejemplo 3: Velocidad (km/h a m/s)
Convierta 13 km/h a m/s.
Solución:
Datos necesarios:
1 km = 1000 m
1 h = 3600 s (o puedes usar 1 h = 60 min y 1 min = 60 s).
\[ 13 \frac{\text{km}}{\text{h}} \left( \frac{1000 \text{ m}}{1 \text{ km}} \right) \left( \frac{1 \text{ h}}{3600 \text{ s}} \right) = 3.61 \frac{\text{m}}{\text{s}} \]
Veamos la solución gráfica paso a paso: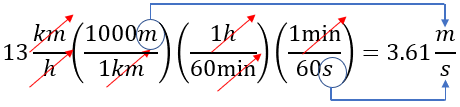
Ejemplo 4: Conversión de Volumen (Galones a cm³)
Convierta 7 galones a centímetros cúbicos.
Solución:
A veces no hay un factor directo, así que usamos un "puente":
1 Galón = 3.785 litros
1 Litro = 1000 cm³
\[ 7 \text{ gal} \left( \frac{3.785 \text{ l}}{1 \text{ gal}} \right) \left( \frac{1000 \text{ cm}^3}{1 \text{ l}} \right) = 26495 \text{ cm}^3 \]
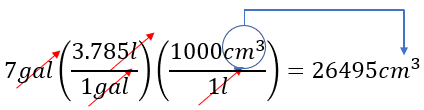
Ejemplo 5: Sistema Inglés (Millas/h a m/s)
Convierta 8 millas/h a m/s.
Solución:
Factores: 1 milla = 1609 m | 1 h = 3600 s.
\[ 8 \frac{\text{millas}}{\text{h}} \left( \frac{1609 \text{ m}}{1 \text{ milla}} \right) \left( \frac{1 \text{ h}}{3600 \text{ s}} \right) = 3.57 \frac{\text{m}}{\text{s}} \]

Más Ejercicios de Práctica (Variados)
Para dominar el tema, necesitamos ver casos de la vida real: pantallas, aviones, masa y dimensiones pequeñas.
Ejemplo 6: Pulgadas a Centímetros
Los fabricantes de pantallas especifican el tamaño dando la longitud de la diagonal en pulgadas. ¿Cuál es la longitud en centímetros de una pantalla de 26 pulgadas?
Solución:
\[ 26 \text{ in} \left( \frac{2.54 \text{ cm}}{1 \text{ in}} \right) = 66.04 \text{ cm} \]
Ejemplo 7: Centímetros a Pulgadas
El diámetro de los discos compactos es de 12 centímetros. ¿A cuánto equivale en pulgadas?
Solución:
\[ 12 \text{ cm} \left( \frac{1 \text{ in}}{2.54 \text{ cm}} \right) = 4.724 \text{ in} \]
Ejemplo 8: Altura de Vuelo (Pies a Metros)
Un piloto de avión informa a sus pasajeros que vuelan a 30,000 pies de altura. ¿A cuántos metros equivale esto?
Solución:
\[ 30000 \text{ ft} \left( \frac{0.3048 \text{ m}}{1 \text{ ft}} \right) = 9144 \text{ m} \]
Ejemplo 9: Distancias Geográficas (km a millas)
El radio de la tierra es de 6370 km. ¿A cuántas millas equivale esto?
Solución:
\[ 6370 \text{ km} \left( \frac{1 \text{ milla}}{1.609 \text{ km}} \right) = 3958.9 \text{ millas} \]
Ejemplo 10: Dimensiones Múltiples y Masa
Un teléfono celular mide 12.38 cm de alto. ¿A cuánto equivale en pulgadas? Además, si tiene una masa de 112 gramos, ¿cuánto es en onzas?
Solución:
Longitud:
\[ 12.38 \text{ cm} \left( \frac{1 \text{ in}}{2.54 \text{ cm}} \right) = 4.87 \text{ in} \]
Masa (1 oz = 28.35 g):
\[ 112 \text{ g} \left( \frac{1 \text{ oz}}{28.35 \text{ g}} \right) = 3.95 \text{ oz} \]
Ejemplo 11: Longitud (km a millas)
Convierta 8.33 km a millas.
Solución:
\[ 8.33 \text{ km} \left( \frac{1 \text{ milla}}{1.609 \text{ km}} \right) = 5.17 \text{ millas} \]
Ejemplo 12: Volumen (Galones a Litros)
Convierta 19.3 gal a litros.
Solución:
\[ 19.3 \text{ gal} \left( \frac{3.785 \text{ l}}{1 \text{ gal}} \right) = 73.05 \text{ l} \]
Ejemplo 13: Masa (kg a Slugs)
Convierta 45 kg a slug (Unidad de masa del sistema inglés).
Solución:
Sabemos que 1 slug = 14.59 kg.
\[ 45 \text{ kg} \left( \frac{1 \text{ slug}}{14.59 \text{ kg}} \right) = 3.08 \text{ slug} \]
Ejemplo 14: Longitud Pequeña (cm a pies)
Convierta 18 cm a pies (ft).
Solución:
\[ 18 \text{ cm} \left( \frac{1 \text{ ft}}{30.48 \text{ cm}} \right) = 0.59 \text{ ft} \]
Ejemplo 15: Pulgadas a Metros
Convierta 27.11 pulgadas a metros.
Solución:
\[ 27.11 \text{ in} \left( \frac{0.0254 \text{ m}}{1 \text{ in}} \right) = 0.688 \text{ m} \]
Ejemplo 16: Masa (Onzas a kg)
Convierta 125 oz a kg.
Solución:
\[ 125 \text{ oz} \left( \frac{0.02835 \text{ kg}}{1 \text{ oz}} \right) = 3.54 \text{ kg} \]
Ejemplo 17: Barriles de Petróleo (BBL a dm³)
Convierta 47.5 barriles (bbl) a decímetros cúbicos.
Solución:
Nota: 1 bbl = 42 galones y 1 galón = 3.785 litros (dm³).
\[ 47.5 \text{ bbl} \left( \frac{42 \text{ gal}}{1 \text{ bbl}} \right) \left( \frac{3.785 \text{ dm}^3}{1 \text{ gal}} \right) = 7551.89 \text{ dm}^3 \]
Ejemplo 18: Conversión de Área (Metros cuadrados a cm²)
Convierta 5 m² a cm².
Solución:
\[ 5 \text{ m}^2 \left( \frac{10,000 \text{ cm}^2}{1 \text{ m}^2} \right) = 50,000 \text{ cm}^2 \]
Ejemplo 19: Densidad (g/cm³ a kg/m³)
Convierta la densidad del agua: 1 g/cm³ a kg/m³.
Solución:
\[ 1 \frac{\text{g}}{\text{cm}^3} \times \left( \frac{1 \text{ kg}}{1000 \text{ g}} \right) \times \left( \frac{1,000,000 \text{ cm}^3}{1 \text{ m}^3} \right) = 1000 \frac{\text{kg}}{\text{m}^3} \]
Ejemplo 20: Presión (Atmósferas a Pascales)
Convierta una presión de 2 atmósferas (atm) a Pascales (Pa).
Solución:
\[ 2 \text{ atm} \left( \frac{101,325 \text{ Pa}}{1 \text{ atm}} \right) = 202,650 \text{ Pa} \]
Ejemplo 21: Fuerza (Newtons a Dinas)
Convierta 25 Newtons (N) a Dinas.
Solución:
\[ 25 \text{ N} \left( \frac{10^5 \text{ dinas}}{1 \text{ N}} \right) = 2.5 \times 10^6 \text{ dinas} \]
Ejemplo 22: Energía (Joules a Calorías)
Convierta 50 Joules (J) a calorías (cal).
Solución:
\[ 50 \text{ J} \left( \frac{1 \text{ cal}}{4.184 \text{ J}} \right) = 11.95 \text{ cal} \]
Ejemplo 23: Potencia (HP a Watts)
Convierta 2 HP (caballos de fuerza) a Watts.
Solución:
\[ 2 \text{ HP} \left( \frac{746 \text{ W}}{1 \text{ HP}} \right) = 1492 \text{ W} \]
Ejemplo 24: Presión de Neumáticos (PSI a Pascales)
Convierta 35 PSI (lb/in²) a Pascales (Pa).
Solución:
\[ 35 \text{ PSI} \left( \frac{6895 \text{ Pa}}{1 \text{ PSI}} \right) = 241,325 \text{ Pa} \]
Ejemplo 25: Caudal (Litros/min a m³/s)
Convierta un flujo de 40 L/min a m³/s.
Solución:
\[ 40 \frac{\text{L}}{\text{min}} \times \left( \frac{0.001 \text{ m}^3}{1 \text{ L}} \right) \times \left( \frac{1 \text{ min}}{60 \text{ s}} \right) = 6.67 \times 10^{-4} \frac{\text{m}^3}{\text{s}} \]
Ejemplo 26: Velocidad Angular (rpm a rad/s)
Convierta 1200 rpm (revoluciones por minuto) a rad/s.
Solución:
\[ 1200 \frac{\text{rev}}{\text{min}} \times \left( \frac{2\pi \text{ rad}}{1 \text{ rev}} \right) \times \left( \frac{1 \text{ min}}{60 \text{ s}} \right) = 40\pi \text{ rad/s} \approx 125.66 \text{ rad/s} \]
Ejemplo 27: Aceleración (m/s² a ft/s²)
Convierta la gravedad de 9.8 m/s² a ft/s².
Solución:
\[ 9.8 \frac{\text{m}}{\text{s}^2} \left( \frac{3.281 \text{ ft}}{1 \text{ m}} \right) = 32.15 \frac{\text{ft}}{\text{s}^2} \]
Ejemplo 28: Área Agraria (Hectáreas a m²)
Convierta 2 Hectáreas a metros cuadrados.
Solución:
\[ 2 \text{ ha} \left( \frac{10,000 \text{ m}^2}{1 \text{ ha}} \right) = 20,000 \text{ m}^2 \]
Ejemplo 29: Energía Térmica (BTU a Joules)
Convierta 12,000 BTU a Joules.
Solución:
\[ 12,000 \text{ BTU} \left( \frac{1055 \text{ J}}{1 \text{ BTU}} \right) = 1.266 \times 10^7 \text{ J} \]
Ejemplo 30: Consumo de Combustible (Complejo)
Convierta 12 km/L a millas por galón (mpg).
Solución:
\[ 12 \frac{\text{km}}{\text{L}} \times \left( \frac{1 \text{ mi}}{1.609 \text{ km}} \right) \times \left( \frac{3.785 \text{ L}}{1 \text{ gal}} \right) = 28.22 \text{ mpg} \]
Problemas Propuestos para Practicar (¡Ponte a Prueba!)
¿Crees que ya lo dominas? Intenta resolver estos ejercicios por tu cuenta antes de ver la solución oculta.
Problema 31: Longitud
Convierta 6 km a pies.
▶︎ Haz clic aquí para ver la solución
1 km = 3280.84 pies.
\[ 6 \text{ km} \left( \frac{3280.84 \text{ ft}}{1 \text{ km}} \right) = 19685 \text{ ft} \]
Problema 32: Velocidad
Convierta 5 millas/h a m/s.
▶︎ Haz clic aquí para ver la solución
\[ 5 \frac{\text{mi}}{\text{h}} \left( \frac{1609 \text{ m}}{1 \text{ mi}} \right) \left( \frac{1 \text{ h}}{3600 \text{ s}} \right) = 2.23 \frac{\text{m}}{\text{s}} \]
Problema 33: Caudal (Volumen/Tiempo)
Convierta 96500 cm³/min a gal/s.
▶︎ Haz clic aquí para ver la solución
1 gal = 3785 cm³.
\[ 96500 \frac{\text{cm}^3}{\text{min}} \left( \frac{1 \text{ gal}}{3785 \text{ cm}^3} \right) \left( \frac{1 \text{ min}}{60 \text{ s}} \right) = 0.425 \frac{\text{gal}}{\text{s}} \]
Problema 34: Longitud
Convierta 1.2 km a pulgadas.
▶︎ Haz clic aquí para ver la solución
1 km = 39370.1 pulgadas.
\[ 1.2 \text{ km} \times 39370.1 = 47244 \text{ in} \]
Problema 35: Caudal Complejo
Convierta 0.94 gal/s a cm³/hr.
▶︎ Haz clic aquí para ver la solución
\[ 0.94 \frac{\text{gal}}{\text{s}} \left( \frac{3785 \text{ cm}^3}{1 \text{ gal}} \right) \left( \frac{3600 \text{ s}}{1 \text{ h}} \right) = 12,808,440 \frac{\text{cm}^3}{\text{h}} \]
Problema 36: Velocidad Alta
Convierta 1500 km/s a millas/min.
▶︎ Haz clic aquí para ver la solución
\[ 1500 \frac{\text{km}}{\text{s}} \left( \frac{0.6214 \text{ mi}}{1 \text{ km}} \right) \left( \frac{60 \text{ s}}{1 \text{ min}} \right) = 55,926 \frac{\text{mi}}{\text{min}} \]
Descargar PDF con 50 Ejercicios Resueltos
Si necesitas practicar más para tu examen, hemos preparado un cuadernillo completo.
🔒 Descarga segura desde Google Drive • 100% Gratuito
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado la Conversión de Unidades. Ya sabes usar factores de conversión para longitud, masa, tiempo y unidades compuestas.
Este tema es fundamental para entender temas más avanzados. Te recomendamos visitar nuestro artículo pilar sobre Unidades y Mediciones para aplicar estas conversiones en sistemas de fuerzas.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Me ayudó ah reforzar mis conocimientos
★★★★★
-
Agradezco mucho que comparta este material, gracias y bendiciones.
★★★★★
-
👍
★★★★★
130 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar