Distancia entre Dos Puntos - Ejercicios Resueltos
Dentro de la Geometría Analítica, pocos conceptos son tan fundamentales como saber medir el espacio. Comprender la distancia entre dos puntos no es solo un requisito para aprobar el examen; es la base para entender vectores, física cinemática y hasta cómo funciona el GPS de tu celular.
En este artículo vamos a dominar este tema desde cero: analizaremos la fórmula, deduciremos su origen geométrico y resolveremos ejercicios que van desde lo básico hasta problemas tipo examen.
¿Qué aprenderás hoy?
En este post dominarás:
- La deducción lógica de la fórmula (sin memorizar por memorizar).
- Cómo resolver problemas cuando la distancia es horizontal, vertical o diagonal.
- Cómo encontrar coordenadas faltantes usando álgebra.
- Un banco de ejercicios para practicar y un PDF descargable.
Fórmula de la Distancia entre dos Puntos
Para ir directo al grano, si buscas la herramienta matemática para calcular la longitud del segmento que une a dos puntos \(P_1(x_1, y_1)\) y \(P_2(x_2, y_2)\) en el plano cartesiano, esta es la definición formal:
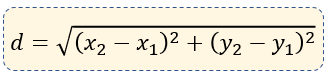
Fórmula General
La distancia \(d\) entre dos puntos cualesquiera del plano se calcula mediante la raíz cuadrada de la suma de los cuadrados de las diferencias de sus coordenadas:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Antes de pasar a los ejercicios complejos, es vital entender que existen tres casos posibles al medir distancias. Analicémoslos uno por uno.
Caso 1: Distancia Horizontal
Imaginemos que tenemos dos pares ordenados \(P_1(x_1, y_1)\) y \(P_2(x_2, y_2)\) que forman una recta paralela al eje "x".
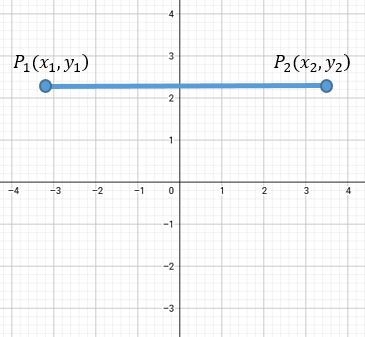
Como puedes ver en la imagen, la altura (y) no cambia. Para calcular la distancia, simplemente restamos las abscisas (x).
\[ d = |x_2 - x_1| \]
Nota: Usamos valor absoluto porque una distancia física nunca puede ser negativa.
Caso 2: Distancia Vertical
De forma similar, si los puntos comparten la misma coordenada x (están uno encima del otro), la distancia es la diferencia absoluta de sus ordenadas.
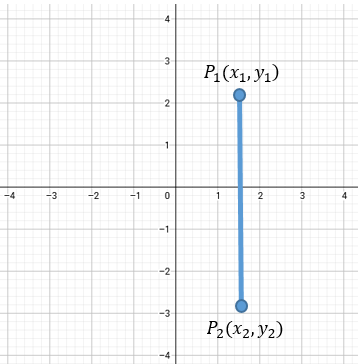
Aquí la fórmula se simplifica a:
\[ d = |y_2 - y_1| \]
Caso 3: Distancia General (Diagonal)
Aquí es donde la magia ocurre. Cuando los puntos no están alineados ni vertical ni horizontalmente, forman una diagonal.
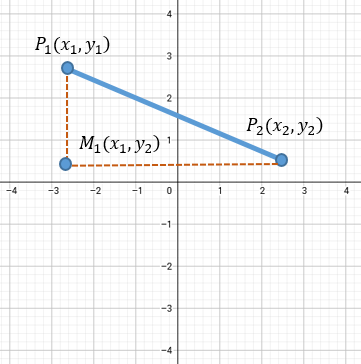
Si observas el gráfico de arriba con atención, verás que se forma un Triángulo Rectángulo:
1. La base del triángulo es la diferencia de las x: \(x_2 - x_1\)
2. La altura del triángulo es la diferencia de las y: \(y_2 - y_1\)
3. La distancia \(d\) es la Hipotenusa.
Por lo tanto, aplicando el Teorema de Pitágoras (\(c^2 = a^2 + b^2\)), llegamos a nuestra fórmula maestra:
\[ d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \]
Despejando el cuadrado como raíz, obtenemos la fórmula que todos conocemos.
Ejercicios Resueltos de Distancia entre Dos Puntos
Vamos a poner en práctica la teoría con los gráficos correspondientes para que visualices el problema.
Ejemplo 1: Cálculo básico (Recta Horizontal)
Hallar la distancia entre los puntos \(P_1(-5, 3)\) y \(P_2(4, 3)\).
Solución:
Observando las coordenadas, vemos que \(y\) no cambia (es 3 en ambos). Es una recta horizontal.
\[ d = |x_2 - x_1| = |4 - (-5)| = |4 + 5| = 9 \]
Resultado: La distancia es de 9 unidades.
Ejemplo 2: Aplicando la Fórmula General
Hallar la distancia entre los puntos \(P_1(-4, 3)\) y \(P_2(3, 2)\).
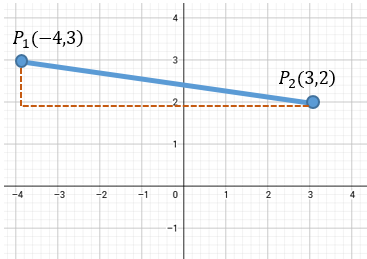
Solución:
Aquí las coordenadas son distintas. Elegimos \(P_1\) como inicial y \(P_2\) como final y sustituimos en la fórmula:
\[ d = \sqrt{(3 - (-4))^2 + (2 - 3)^2} \]
\[ d = \sqrt{(3 + 4)^2 + (-1)^2} \]
\[ d = \sqrt{(7)^2 + 1} \]
\[ d = \sqrt{49 + 1} = \sqrt{50} \]
Simplificando o calculando:
\[ d \approx 7.071 \text{ unidades} \]
Ejemplo 3: Coordenadas Negativas
Encuentre la distancia entre los puntos \(P_1(-2, 3)\) y \(P_2(3, -3)\).
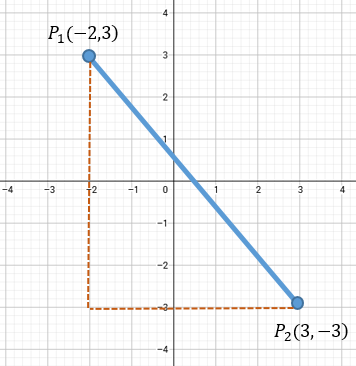
Solución:
Ten mucho cuidado con los signos negativos al sustituir en la fórmula. Recuerda que \(-(-a) = +a\).
\[ d = \sqrt{(3 - (-2))^2 + (-3 - 3)^2} \]
\[ d = \sqrt{(3 + 2)^2 + (-6)^2} \]
\[ d = \sqrt{(5)^2 + 36} \]
\[ d = \sqrt{25 + 36} = \sqrt{61} \]
\[ d \approx 7.810 \text{ unidades} \]
⚠️ Punto Importante: Problema Inverso
El siguiente ejercicio es un clásico de examen de admisión. No te piden la distancia, sino una coordenada faltante. Requiere un despeje algebraico.
Ejemplo 4: Hallar una coordenada desconocida (Nivel Avanzado)
Uno de los extremos de un segmento de longitud igual a 17 es el punto \(A(1, -11)\). Si la ordenada del otro extremo es 4, halla su abscisa (\(x_2\)).
Solución:
Datos: \(d = 17\), \(P_1(1, -11)\), \(P_2(x_2, 4)\). Nuestra incógnita es \(x_2\).
Sustituimos en la fórmula elevando al cuadrado para eliminar la raíz:
\[ 17^2 = (x_2 - 1)^2 + (4 - (-11))^2 \]
\[ 289 = (x_2 - 1)^2 + (15)^2 \]
\[ 289 = (x_2 - 1)^2 + 225 \]
Despejamos el término con la x:
\[ 289 - 225 = (x_2 - 1)^2 \]
\[ 64 = (x_2 - 1)^2 \]
Sacamos raíz cuadrada a ambos lados (considerando el signo más/menos):
\[ \pm\sqrt{64} = x_2 - 1 \]
\[ \pm 8 = x_2 - 1 \]
Esto nos da dos posibles soluciones, tal como se ve en la gráfica siguiente:
- Caso 1: \(8 = x_2 - 1 \Rightarrow x_2 = 9\)
- Caso 2: \(-8 = x_2 - 1 \Rightarrow x_2 = -7\)
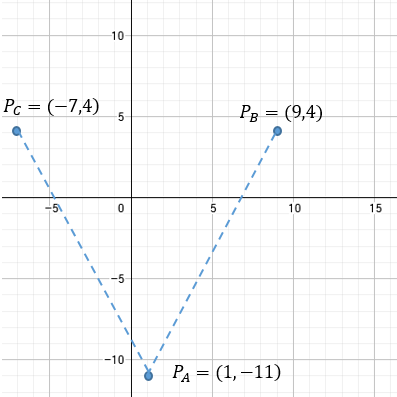
Resultado: Existen dos puntos que cumplen la condición: \(P_B(9, 4)\) y \(P_C(-7, 4)\).
Ejemplo 5: Distancia con coordenadas mixtas
Calcula la distancia entre los puntos \(A(-3, 5)\) y \(B(3, -3)\).

Solución:
Este ejercicio es ideal para practicar la ley de los signos. Identificamos nuestros datos:
- \(x_1 = -3, \quad y_1 = 5\)
- \(x_2 = 3, \quad y_2 = -3\)
Sustituimos en la fórmula general:
\[ d = \sqrt{(3 - (-3))^2 + (-3 - 5)^2} \]
Ten cuidado aquí: menos por menos da más (\(-\) por \(-\) es \(+\)):
\[ d = \sqrt{(3 + 3)^2 + (-8)^2} \]
\[ d = \sqrt{(6)^2 + 64} \]
\[ d = \sqrt{36 + 64} = \sqrt{100} \]
Resultado: La distancia es de 10 unidades.
Ejemplo 6: Cálculo del Perímetro de un Triángulo
Dados los vértices de un triángulo \(A(-2, 1)\), \(B(4, 1)\) y \(C(1, 5)\), calcula su perímetro.
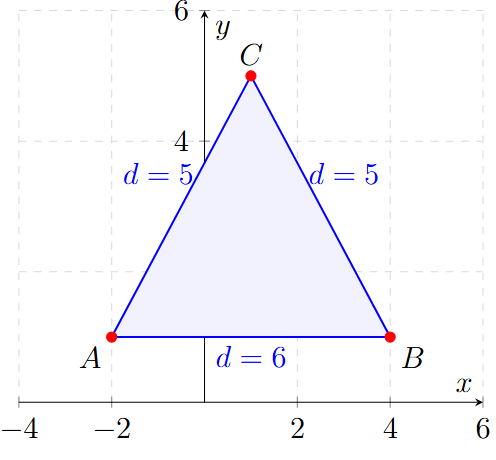
Solución:
Para hallar el perímetro, necesitamos sumar la longitud de los tres lados. Calcularemos la distancia entre cada par de puntos.
1. Distancia lado AB (Horizontal):
\[ d_{AB} = \sqrt{(4 - (-2))^2 + (1 - 1)^2} = \sqrt{(6)^2} = 6 \]
2. Distancia lado AC:
\[ d_{AC} = \sqrt{(1 - (-2))^2 + (5 - 1)^2} = \sqrt{(3)^2 + (4)^2} = \sqrt{9 + 16} = 5 \]
3. Distancia lado BC:
\[ d_{BC} = \sqrt{(1 - 4)^2 + (5 - 1)^2} = \sqrt{(-3)^2 + (4)^2} = \sqrt{9 + 16} = 5 \]
Finalmente, sumamos las distancias:
\[ P = 6 + 5 + 5 = 16 \]
Resultado: El perímetro del triángulo es de 16 unidades. (Como dato extra: al tener dos lados iguales, es un triángulo isósceles).
Ejemplo 7: Distancia al Origen
Determina la distancia que existe entre el origen del plano cartesiano y el punto \(P(5, -12)\).

Solución:
Recordemos que el "Origen" tiene coordenadas \((0,0)\). Esto simplifica mucho nuestra fórmula, ya que \(x_1\) y \(y_1\) se vuelven cero.
\[ d = \sqrt{(x_2 - 0)^2 + (y_2 - 0)^2} = \sqrt{x^2 + y^2} \]
Sustituimos las coordenadas del punto P:
\[ d = \sqrt{(5)^2 + (-12)^2} \]
\[ d = \sqrt{25 + 144} \]
\[ d = \sqrt{169} \]
Resultado: La distancia es de 13 unidades.
Ejemplo 8: Demostración de Colinealidad
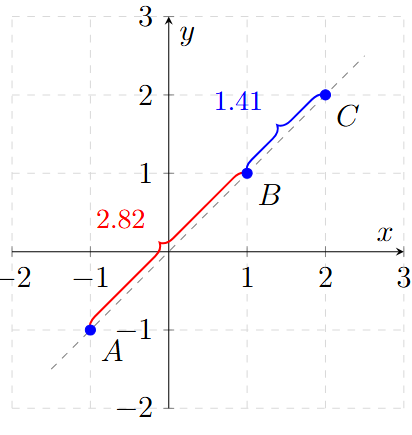
Demuestra matemáticamente si los puntos \(A(-1, -1)\), \(B(1, 1)\) y \(C(2, 2)\) son colineales (están en la misma línea recta).
Solución:
Para que tres puntos sean colineales, la suma de las distancias de los segmentos más cortos debe ser igual a la distancia del segmento total más largo. Es decir: \(d(A,B) + d(B,C) = d(A,C)\).
Calculamos \(d(A,B)\):
\[ d_{AB} = \sqrt{(1 - (-1))^2 + (1 - (-1))^2} = \sqrt{2^2 + 2^2} = \sqrt{8} \approx 2.828 \]
Calculamos \(d(B,C)\):
\[ d_{BC} = \sqrt{(2 - 1)^2 + (2 - 1)^2} = \sqrt{1^2 + 1^2} = \sqrt{2} \approx 1.414 \]
Calculamos la total \(d(A,C)\):
\[ d_{AC} = \sqrt{(2 - (-1))^2 + (2 - (-1))^2} = \sqrt{3^2 + 3^2} = \sqrt{18} \approx 4.242 \]
Comprobamos la suma:
\[ 2.828 + 1.414 = 4.242 \]
Resultado: Como la suma coincide, confirmamos que los puntos SÍ son colineales.
Ejemplo 9: Radio de una Circunferencia
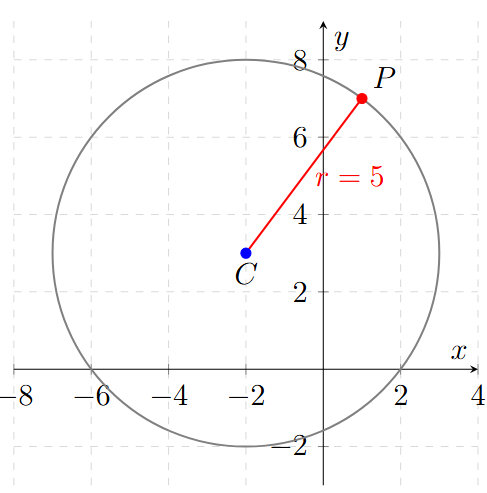
El centro de un círculo está en \(C(-2, 3)\). Si el círculo pasa por el punto \(P(1, 7)\), ¿cuánto mide su radio?
Solución:
El radio de un círculo es, por definición, la distancia desde el centro hasta cualquier punto del borde. Por lo tanto, solo debemos calcular la distancia entre C y P.
\[ r = d(C,P) = \sqrt{(1 - (-2))^2 + (7 - 3)^2} \]
\[ r = \sqrt{(3)^2 + (4)^2} \]
\[ r = \sqrt{9 + 16} = \sqrt{25} \]
Resultado: El radio del círculo es de 5 unidades.
Ejemplo 10: Hallar ordenada 'y' con despeje cuadrático
La distancia entre los puntos \(A(2, 3)\) y \(B(5, y)\) es de 5 unidades. Calcula el valor de la ordenada \(y\).

Solución:
Este es un problema inverso. Conocemos la distancia (\(d=5\)) pero desconocemos una coordenada.
\[ 5 = \sqrt{(5 - 2)^2 + (y - 3)^2} \]
Elevamos al cuadrado ambos lados para eliminar la raíz:
\[ 25 = (3)^2 + (y - 3)^2 \]
\[ 25 = 9 + (y - 3)^2 \]
Pasamos el 9 restando:
\[ 25 - 9 = (y - 3)^2 \]
\[ 16 = (y - 3)^2 \]
Sacamos raíz cuadrada (considerando \(\pm\)):
\[ \pm 4 = y - 3 \]
Esto genera dos soluciones:
- \(y_1 = 4 + 3 = 7\)
- \(y_2 = -4 + 3 = -1\)
Resultado: La ordenada puede ser 7 o -1.
Ejemplo 11: Tipo de Triángulo por sus lados
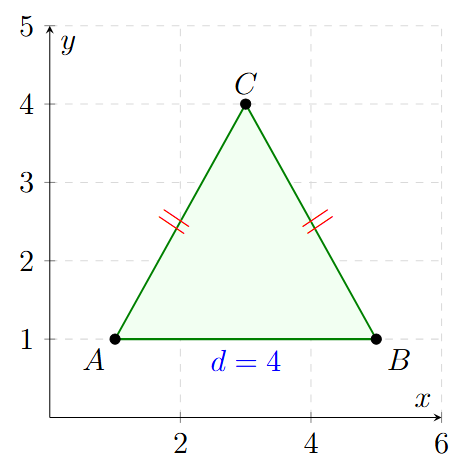
Comprueba si el triángulo con vértices \(A(1, 1)\), \(B(5, 1)\) y \(C(3, 4)\) es equilátero, isósceles o escaleno.
Solución:
Calculamos la longitud de sus tres lados:
1. \(d(A,B) = |5 - 1| = 4\) (Es horizontal).
2. \(d(A,C) = \sqrt{(3 - 1)^2 + (4 - 1)^2} = \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13}\)
3. \(d(B,C) = \sqrt{(3 - 5)^2 + (4 - 1)^2} = \sqrt{(-2)^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13}\)
Resultado: Dado que tiene dos lados iguales (\(\sqrt{13}\)) y uno diferente (\(4\)), es un triángulo isósceles.
Ejemplo 12: Aplicación Física (Desplazamiento)
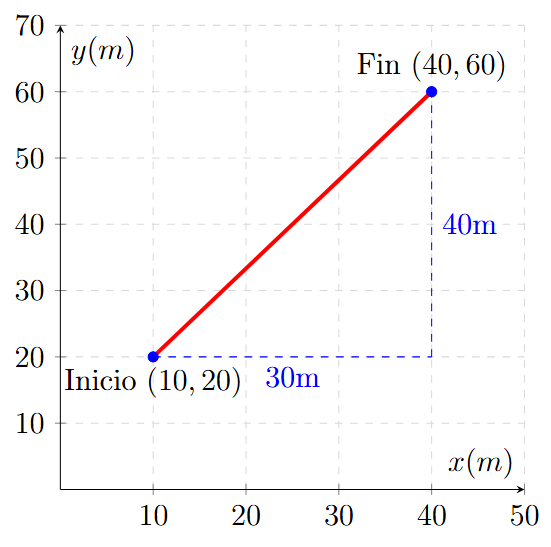
Un objeto se mueve desde la posición \(A(10, 20)\) hasta la posición \(B(40, 60)\) en un mapa de coordenadas (en metros). ¿Cuál fue la magnitud de su desplazamiento?
Solución:
El desplazamiento es la distancia en línea recta entre el punto de inicio y el final.
\[ d = \sqrt{(40 - 10)^2 + (60 - 20)^2} \]
\[ d = \sqrt{(30)^2 + (40)^2} \]
\[ d = \sqrt{900 + 1600} \]
\[ d = \sqrt{2500} \]
Resultado: La magnitud del desplazamiento es de 50 metros.
Banco de Práctica: +20 Ejercicios de Distancia entre dos Puntos
¿Listo para ponerte a prueba? Hemos seleccionado ejercicios clave para que practiques. Intenta resolverlos antes de ver la solución.
Ejercicio Propuesto 1
Calcula la distancia exacta entre los puntos \(A(-2, 5)\) y \(B(4, -3)\).
Ver Solución
\[ d = \sqrt{(4 - (-2))^2 + (-3 - 5)^2} \]
\[ d = \sqrt{6^2 + (-8)^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
Ejercicio Propuesto 2
Demuestra si el triángulo formado por \(A(1, 2)\), \(B(4, 6)\) y \(C(1, 6)\) es un triángulo rectángulo calculando sus lados.
Ver Solución
Calculamos las 3 distancias:
1. \(d(A,B) = \sqrt{(3)^2 + (4)^2} = 5\)
2. \(d(B,C) = \sqrt{(-3)^2 + (0)^2} = 3\)
3. \(d(A,C) = \sqrt{(0)^2 + (4)^2} = 4\)
Como \(3^2 + 4^2 = 5^2\) (9+16=25), cumple Pitágoras. Sí es triángulo rectángulo.
Descarga la Guía Completa en PDF (Más ejercicios)
La IA puede darte una respuesta rápida, pero no puede estudiar por ti. He preparado un Cuadernillo de Trabajo en PDF que incluye:
- Resumen de fórmulas.
- Los ejemplos de este post.
- Banco de 20 ejercicios propuestos con sus respuestas para imprimir y rayar.
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Ya dominas el cálculo de distancias en el plano. Este es el primer "superpoder" para navegar en la Geometría Analítica.
Ahora que sabes medir distancias, el siguiente paso lógico es aprender a encontrar el punto exacto a la mitad del camino. Te invito a continuar con nuestro artículo sobre:
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
El enunciado del ejemplo 3 no concuerda con su solución, por favor corregir.
-
Excelente artículo , muy didáctico y claro
congratulaciones ! -
El ejercicio 3 por que cambia el 3 por - 3?
-
Quedaría (3-(-3)
-
-
Es muy interesante
-
Alguien me ayuda con los míos no entiendo ?
-
-
En el ejercicio 3, la información de la recta no concuerda con la pregunta, no colocaron el -3
22 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar