Ecuación de la Elipse con Centro fuera del Origen
Si ya has dominado la elipse con centro en el origen, ¡felicidades! Has dado el primer paso. Pero en el mundo real y en los exámenes más complejos de geometría analítica, las figuras rara vez se quedan quietas en el centro del plano cartesiano (0,0). A veces, necesitan moverse.
Hoy vamos a subir de nivel. Aprenderemos a dominar la Ecuación de la Elipse con Centro fuera del Origen, representada por las coordenadas \(C(h,k)\). Aunque las fórmulas parezcan más largas, la lógica sigue siendo exactamente la misma. ¿Estás listo para convertirte en un experto? ¡Vamos allá!
Definición de Elipse con Centro (h,k)
Una elipse con centro fuera del origen es aquella cuyo punto central no coincide con la coordenada \((0,0)\), sino que se encuentra en un punto arbitrario del plano cartesiano denotado como \(C(h,k)\).
Para abordar este tema, es vital que recuerdes que los elementos geométricos (vértices, focos) simplemente se "desplazan" sumando las unidades \(h\) en el eje horizontal y \(k\) en el eje vertical.
Ecuación Ordinaria y Elementos de la Elipse (h,k)
A diferencia de la elipse centrada en el origen, aquí veremos cómo los valores \(h\) y \(k\) acompañan a \(x\) y \(y\) respectivamente dentro de los binomios al cuadrado. Existen dos casos fundamentales: cuando la elipse es horizontal y cuando es vertical.
⚠️ Punto Importante: ¿Cómo saber si es Horizontal o Vertical?
La clave siempre está en el denominador mayor (\(a^2\)).
- Si el número mayor está debajo de la \(x\), la elipse es Horizontal.
- Si el número mayor está debajo de la \(y\), la elipse es Vertical.
1. Elipse Horizontal con centro en (h,k)
Cuando el eje focal (la línea que une los focos) es paralelo al eje X, utilizamos la siguiente ecuación estándar:
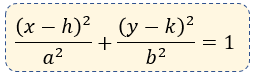
Elementos clave:
Como el movimiento principal es horizontal, las coordenadas que cambian son las de las abscisas (\(x\)), afectadas por el valor \(h\).
- Vértices (Eje Mayor): \[ V(h\pm a, k) \]
- Focos: \[ F(h\pm c, k) \]
- Extremos del Eje Menor: \[ B(h, k\pm b) \]
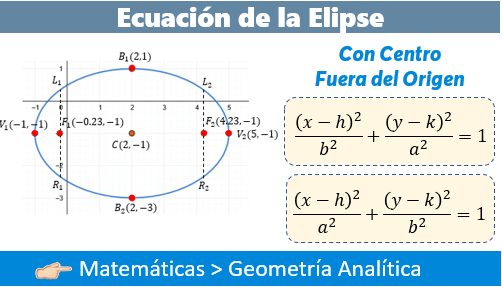
2. Elipse Vertical con centro en (h,k)
Cuando el eje focal es paralelo al eje Y, el valor de \(a^2\) (el mayor) estará dividiendo a las \(y\).
Elementos clave:
Aquí el movimiento principal es vertical, por lo tanto, las alteraciones se dan en las ordenadas (\(y\)), afectadas por \(k\).
- Vértices (Eje Mayor): \[ V(h, k\pm a) \]
- Focos: \[ F(h, k\pm c) \]
- Extremos del Eje Menor: \[ B(h\pm b, k) \]
Ecuación General de la Elipse
Muchas veces, los ejercicios no nos dan la ecuación "bonita" (ordinaria), sino desarrollada. Esta se conoce como la Ecuación General:
\[ Ax^2 + Cy^2 + Dx + Ey + F = 0 \]
Para que esta ecuación represente una elipse, debe cumplirse una regla de oro: \(A \neq C\), pero ambos deben tener el mismo signo.
Ejercicios Resueltos de Elipse fuera del Origen
La mejor forma de aprender es practicando. A continuación, resolveremos 7 ejemplos paso a paso que cubren desde lo más básico hasta casos especiales con excentricidad y lado recto.
Ejemplo 1: De la Ecuación General a la Ordinaria
Determine los elementos y la gráfica de una elipse dada por la ecuación general:
\[ 4x^2 + 9y^2 - 16x + 18y - 11 = 0 \]
Solución:
Este es el procedimiento estándar que debes dominar. Usaremos la técnica de completar el trinomio cuadrado perfecto (TCP).
Paso 1: Agrupar términos.
Agrupamos las \(x\) con las \(x\), las \(y\) con las \(y\), y pasamos el término independiente (la constante) al lado derecho de la igualdad.
\[ (4x^2 - 16x) + (9y^2 + 18y) = 11 \]
Paso 2: Factorizar los coeficientes principales.
Necesitamos que \(x^2\) y \(y^2\) estén "solas" dentro del paréntesis para poder completar el cuadrado. Factorizamos el 4 en el primer grupo y el 9 en el segundo.
\[ 4(x^2 - 4x) + 9(y^2 + 2y) = 11 \]
Paso 3: Completar el Trinomio Cuadrado Perfecto.
Aquí viene el truco. Tomamos el segundo término de cada paréntesis, lo dividimos entre 2 y lo elevamos al cuadrado.
- Para las \(x\): \((-4/2)^2 = (-2)^2 = 4\)
- Para las \(y\): \((2/2)^2 = (1)^2 = 1\)
Ahora agregamos estos números dentro de los paréntesis.
💡 ¡Ojo con el balanceo!
Si agregas un número dentro del paréntesis, estás afectando la ecuación. Como hay un número multiplicando afuera (el 4 y el 9), debes sumar al lado derecho ese mismo valor multiplicado.
Ejemplo: Si agregas 4 adentro, y afuera hay un 4, en realidad sumaste \(4 \times 4 = 16\).
\[ 4(x^2 - 4x + 4) + 9(y^2 + 2y + 1) = 11 + 16 + 9 \]
Si te fijas, sumamos 16 (que es \(4 \times 4\)) y sumamos 9 (que es \(9 \times 1\)).
Paso 4: Factorizar a binomios al cuadrado.
Simplificamos la ecuación:
\[ 4(x - 2)^2 + 9(y + 1)^2 = 36 \]
Paso 5: Igualar a 1.
Para llegar a la forma ordinaria, dividimos toda la ecuación entre 36.
\[ \frac{4(x - 2)^2}{36} + \frac{9(y + 1)^2}{36} = \frac{36}{36} \]
Simplificando fracciones (\(4/36 = 1/9\) y \(9/36 = 1/4\)):
\[ \frac{(x - 2)^2}{9} + \frac{(y + 1)^2}{4} = 1 \]
Análisis de Resultados:
Ahora tenemos la ecuación ordinaria. Podemos extraer la información:
- Orientación: Como el denominador mayor (9) está bajo la \(x\), es una Elipse Horizontal.
- Valores de a y b:
\[ a^2 = 9 \Rightarrow a = 3 \]
\[ b^2 = 4 \Rightarrow b = 2 \] - Centro (h,k):
De \((x-2)\) obtenemos \(h=2\).
De \((y+1)\) obtenemos \(k=-1\). (Recuerda cambiar el signo).
Centro: \( C(2, -1) \)
Calculamos \(c\) (distancia focal) usando \( c = \sqrt{a^2 - b^2} \):
\[ c = \sqrt{9 - 4} = \sqrt{5} \approx 2.23 \]
Cálculo de Elementos:
1️⃣ Vértices \(V(h\pm a, k)\):
\(V_1(2+3, -1) \to V_1(5, -1)\)
\(V_2(2-3, -1) \to V_2(-1, -1)\)
2️⃣ Focos \(F(h\pm c, k)\):
\(F_1(2+2.23, -1) \to F_1(4.23, -1)\)
\(F_2(2-2.23, -1) \to F_2(-0.23, -1)\)
3️⃣ Lado Recto:
\[ LR = \frac{2b^2}{a} = \frac{2(4)}{3} = \frac{8}{3} \approx 2.66 \]
Gráfica: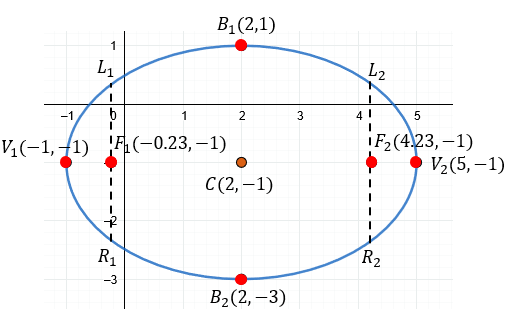
Ejemplo 2: Encontrar la ecuación dados los elementos
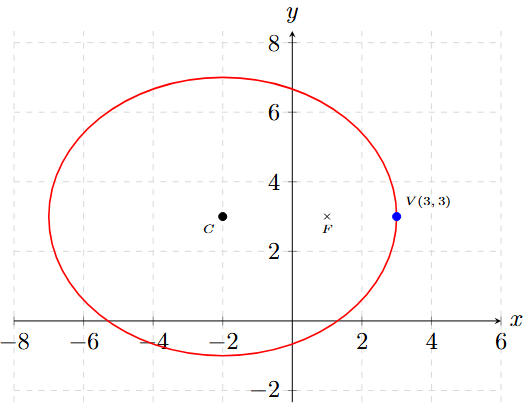
Encuentra la ecuación ordinaria de la elipse que tiene su centro en \(C(-2, 3)\), uno de sus vértices en \(V(3, 3)\) y uno de sus focos en \(F(1, 3)\).
Solución:
Este problema requiere análisis visual. No te lances a las fórmulas sin pensar qué tipo de elipse es.
Paso 1: Identificar la orientación.
Observa las coordenadas:
Centro: \((-2, 3)\)
Vértice: \((3, 3)\)
Foco: \((1, 3)\)
¿Qué coordenada se mantiene constante? ¡La \(y\) siempre vale 3! Si los puntos cambian solo en \(x\), la elipse se extiende horizontalmente.
\(\Rightarrow\) Es una Elipse Horizontal.
Paso 2: Calcular \(a\) y \(c\).
La distancia del Centro al Vértice es \(a\):
\[ a = |3 - (-2)| = |3 + 2| = 5 \]
La distancia del Centro al Foco es \(c\):
\[ c = |1 - (-2)| = |1 + 2| = 3 \]
Paso 3: Calcular \(b\).
Usamos la relación fundamental de la elipse \(a^2 = b^2 + c^2\), despejando \(b\):
\[ b = \sqrt{a^2 - c^2} \]
\[ b = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 \]
Paso 4: Sustituir en la fórmula.
Usamos la ecuación horizontal con \(C(-2, 3)\):
\[ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 \]
\[ \frac{(x - (-2))^2}{5^2} + \frac{(y - 3)^2}{4^2} = 1 \]
\[ \frac{(x + 2)^2}{25} + \frac{(y - 3)^2}{16} = 1 \]
¡Y listo! Esa es nuestra ecuación.
Más Casos de Estudio: Dominando la Elipse 🚀
A veces los problemas no nos dan la ecuación directamente, sino pistas como la excentricidad, el lado recto o las coordenadas de los focos. Vamos a ver cómo armar el rompecabezas en estos casos especiales.
Ejemplo 3: Obtener la Ecuación General dados Vértices y Focos
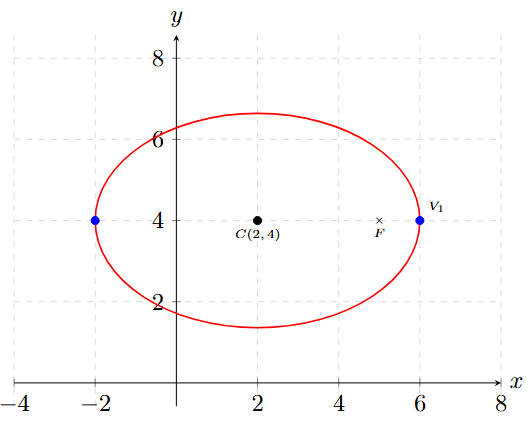
Determina la ecuación general de la elipse cuyos vértices son \(V_1(6, 4)\) y \(V_2(-2, 4)\), y uno de sus focos está en \(F(5, 4)\).
Solución:
Paso 1: Análisis de Coordenadas.
Observa que la coordenada \(y\) es constante (siempre es 4). Esto significa que la elipse está acostada sobre la línea \(y=4\).
\(\Rightarrow\) Elipse Horizontal.
Paso 2: Encontrar el Centro (h,k).
El centro es el punto medio entre los dos vértices.
\[ h = \frac{6 + (-2)}{2} = \frac{4}{2} = 2 \]
\[ k = 4 \]
Centro: \( C(2, 4) \)
Paso 3: Calcular a, c y b.
- Valor de a: Distancia del Centro al Vértice. De \(x=2\) a \(x=6\), hay 4 unidades. \( \Rightarrow a = 4 \).
- Valor de c: Distancia del Centro al Foco. De \(x=2\) a \(x=5\), hay 3 unidades. \( \Rightarrow c = 3 \).
- Valor de b: Despejamos de Pitágoras (\(a^2 = b^2 + c^2\)):
\[ b^2 = a^2 - c^2 = 16 - 9 = 7 \]
\( \Rightarrow b = \sqrt{7} \)
Paso 4: Ecuación Ordinaria.
\[ \frac{(x-2)^2}{16} + \frac{(y-4)^2}{7} = 1 \]
Paso 5: Transformar a General.
Para eliminar fracciones, multiplicamos toda la ecuación por el mínimo común múltiplo de los denominadores (\(16 \times 7 = 112\)).
\[ 7(x-2)^2 + 16(y-4)^2 = 112 \]
Desarrollamos los binomios:
\[ 7(x^2 - 4x + 4) + 16(y^2 - 8y + 16) = 112 \]
Multiplicamos:
\[ 7x^2 - 28x + 28 + 16y^2 - 128y + 256 = 112 \]
Ordenamos e igualamos a cero:
\[ 7x^2 + 16y^2 - 28x - 128y + (28 + 256 - 112) = 0 \]
Resultado Final:
\[ 7x^2 + 16y^2 - 28x - 128y + 172 = 0 \]
Ejemplo 4: Usando la Excentricidad y Focos
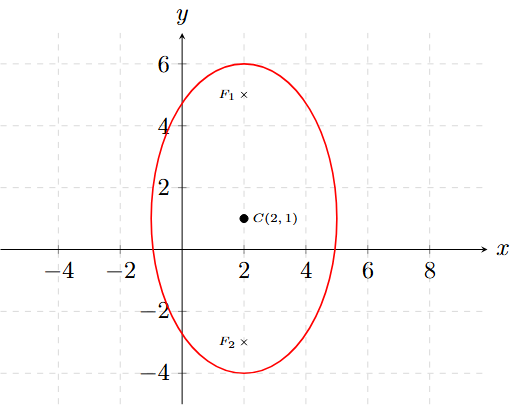
Halla la ecuación de la elipse que tiene sus focos en \(F(2, 5)\) y \(F(2, -3)\), con una excentricidad \(e = 0.8\).
Solución:
Paso 1: Orientación y Centro.
Los focos cambian en \(y\), por lo tanto es una Elipse Vertical.
El centro es el punto medio de los focos:
\[ C\left( \frac{2+2}{2}, \frac{5-3}{2} \right) \to C(2, 1) \]
Paso 2: Obtener c y a.
La distancia entre los focos es \(2c\). De 5 a -3 hay 8 unidades.
\[ 2c = 8 \Rightarrow c = 4 \]
Usamos la fórmula de excentricidad \( e = \frac{c}{a} \):
\[ 0.8 = \frac{4}{a} \]
Despejamos \(a\):
\[ a = \frac{4}{0.8} = 5 \]
Paso 3: Obtener b.
\[ b^2 = a^2 - c^2 = 25 - 16 = 9 \]
\[ b = 3 \]
Paso 4: Sustituir en la fórmula Vertical.
Recordamos que \(a^2\) va debajo de \(y\):
\[ \frac{(x-2)^2}{9} + \frac{(y-1)^2}{25} = 1 \]
Ejemplo 5: Elipse definida por Vértices y Lado Recto
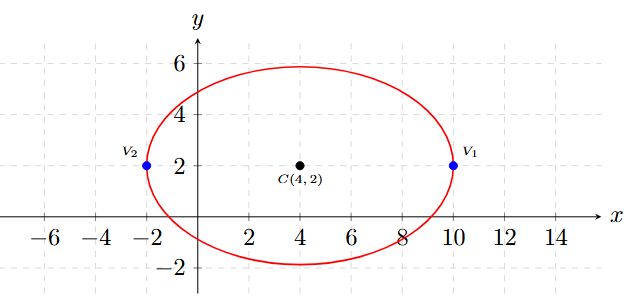
Encuentra la ecuación ordinaria de la elipse cuyos vértices del eje mayor son \(V(10, 2)\) y \(V(-2, 2)\), sabiendo además que la longitud de su lado recto es 5.
Solución:
Este problema es interesante porque mezcla coordenadas con propiedades geométricas. Vamos a desglosarlo.
Paso 1: Determinar la orientación y el Centro.
Observa las coordenadas de los vértices: \( (10, \mathbf{2}) \) y \( (-2, \mathbf{2}) \).
La coordenada \(y\) no cambia. Esto nos indica que la elipse se extiende horizontalmente sobre la línea \(y=2\).
\(\Rightarrow\) Es una Elipse Horizontal.
El centro es siempre el punto medio entre los vértices:
\[ h = \frac{10 + (-2)}{2} = \frac{8}{2} = 4 \]
\[ k = 2 \]
Centro: \( C(4, 2) \)
Paso 2: Calcular el valor de \(a\).
La distancia del centro \( (4,2) \) a cualquiera de los vértices, por ejemplo \( (10,2) \), es el valor de \(a\).
\[ a = 10 - 4 = 6 \]
Paso 3: Usar el Lado Recto para hallar \(b\).
La fórmula del Lado Recto es \( LR = \frac{2b^2}{a} \).
El problema nos dice que \( LR = 5 \) y ya sabemos que \( a = 6 \). Sustituimos:
\[ 5 = \frac{2b^2}{6} \]
Despejamos \( b^2 \):
\[ 5(6) = 2b^2 \]
\[ 30 = 2b^2 \]
\[ b^2 = 15 \]
(No necesitamos sacar la raíz cuadrada de 15, ya que en la fórmula usamos \(b^2\) directamente).
Paso 4: Escribir la Ecuación.
Sustituimos en la estructura horizontal:
\[ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 \]
\[ \frac{(x-4)^2}{36} + \frac{(y-2)^2}{15} = 1 \]
Ejemplo 6: Reducción de General a Ordinaria (Caso Especial)
Reduce la siguiente ecuación general a su forma ordinaria e identifica sus elementos:
\[ x^2 + 4y^2 - 6x + 16y + 21 = 0 \]
Solución:
A veces, al completar el trinomio, los números del lado derecho pueden parecer pequeños o extraños. No te asustes, sigue la metodología.
Paso 1: Agrupar términos.
\[ (x^2 - 6x) + (4y^2 + 16y) = -21 \]
Paso 2: Factorizar coeficientes.
En el primer paréntesis no hay número frente a \(x^2\), así que se queda igual. En el segundo, factorizamos el 4.
\[ (x^2 - 6x) + 4(y^2 + 4y) = -21 \]
Paso 3: Completar cuadrados.
- Para \(x\): \((-6/2)^2 = 9\). Sumamos 9.
- Para \(y\): \((4/2)^2 = 4\). Ojo aquí: al sumar 4 dentro del paréntesis, estamos sumando \(4 \times 4 = 16\) en realidad.
\[ (x^2 - 6x + 9) + 4(y^2 + 4y + 4) = -21 + 9 + 16 \]
Paso 4: Factorizar y Simplificar.
\[ (x - 3)^2 + 4(y + 2)^2 = 4 \]
Nota que el resultado de la suma derecha fue 4 (\(-21+25\)).
Paso 5: Igualar a 1.
Dividimos toda la ecuación entre 4.
\[ \frac{(x - 3)^2}{4} + \frac{4(y + 2)^2}{4} = \frac{4}{4} \]
\[ \frac{(x - 3)^2}{4} + \frac{(y + 2)^2}{1} = 1 \]
Análisis final:
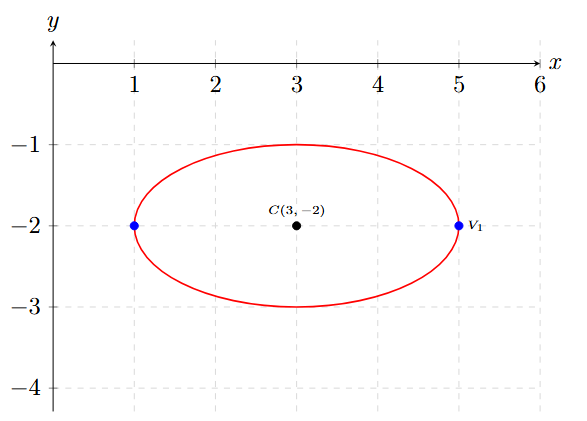
Es una Elipse Horizontal (el 4 es mayor que el 1).
Centro: \( C(3, -2) \).
Semiejes: \( a = 2 \) y \( b = 1 \).
Ejemplo 7: Eje Menor y Foco desalineados
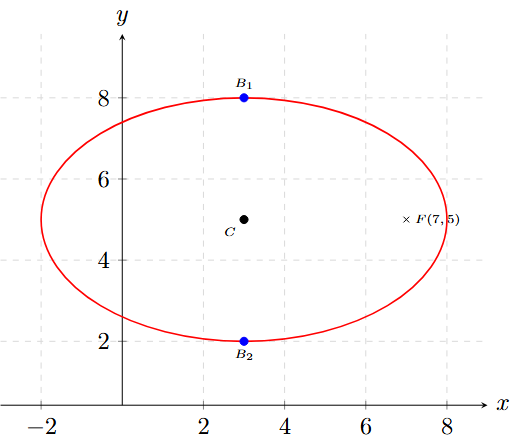
Determina la ecuación de la elipse si los extremos de su eje menor son los puntos \(B_1(3, 8)\) y \(B_2(3, 2)\), y sabemos que uno de sus focos está en \(F(7, 5)\).
Solución:
Este ejercicio requiere mucha atención para no confundir la orientación.
Paso 1: Analizar el Eje Menor.
Los extremos son \( (3, 8) \) y \( (3, 2) \). La coordenada \(x\) no cambia, por lo que el eje menor es una línea vertical.
¡Cuidado! Si el eje menor es vertical, significa que el eje mayor (donde están los focos) es Horizontal.
Paso 2: Encontrar el Centro y \(b\).
El centro es el punto medio del eje menor:
\[ C\left( 3, \frac{8+2}{2} \right) \to C(3, 5) \]
La distancia del centro \( (3,5) \) al extremo \( (3,8) \) es el valor de \(b\).
\[ b = 3 \]
Por lo tanto, \( b^2 = 9 \).
Paso 3: Calcular \(c\) y \(a\).
Sabemos que hay un foco en \( (7, 5) \). La distancia del Centro \( (3,5) \) al Foco \( (7,5) \) es \(c\).
\[ c = 7 - 3 = 4 \]
Ahora usamos Pitágoras para hallar \(a\) (la hipotenusa):
\[ a^2 = b^2 + c^2 \]
\[ a^2 = 9 + 16 = 25 \]
(Entonces \( a = 5 \)).
Paso 4: Ecuación Ordinaria.
Al ser horizontal, \( a^2 \) va debajo de \(x\).
\[ \frac{(x-3)^2}{25} + \frac{(y-5)^2}{9} = 1 \]
Ejercicios Propuestos para Practicar
¿Crees que ya lo tienes? Intenta resolver los siguientes problemas por tu cuenta antes de ver la solución.
Problema Propuesto 1
Halla la ecuación ordinaria de la elipse con ecuación general:
\[ 9x^2 + 4y^2 - 54x - 8y + 49 = 0 \]
Pista: Observa bien qué variable tiene el coeficiente mayor al inicio para intuir la orientación final.
Haz clic aquí para ver la solución
1. Agrupamos:
\(9(x^2 - 6x) + 4(y^2 - 2y) = -49\)
2. Completamos TCP:
\(9(x^2 - 6x + 9) + 4(y^2 - 2y + 1) = -49 + 81 + 4\)
(Nota: \(9 \times 9 = 81\) y \(4 \times 1 = 4\))
3. Factorizamos:
\(9(x - 3)^2 + 4(y - 1)^2 = 36\)
4. Dividimos entre 36:
\(\displaystyle \frac{(x - 3)^2}{4} + \frac{(y - 1)^2}{9} = 1\)
Es una elipse vertical con centro en \(C(3,1)\).
Problema Propuesto 2
Determina las coordenadas de los focos de la siguiente elipse:
\[ \frac{(x+1)^2}{16} + \frac{(y-2)^2}{25} = 1 \]
Haz clic aquí para ver la solución
1. Identificamos orientación:
El número mayor (25) está bajo \(y\). Es Vertical.
\(a^2 = 25 \Rightarrow a=5\)
\(b^2 = 16 \Rightarrow b=4\)
Centro \(h=-1, k=2\).
2. Calculamos c:
\(c = \sqrt{25 - 16} = \sqrt{9} = 3\)
3. Coordenadas Focos \(F(h, k\pm c)\):
\(F_1(-1, 2+3) \to F(-1, 5)\)
\(F_2(-1, 2-3) \to F(-1, -1)\)
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado la Ecuación de la Elipse con Centro fuera del Origen. Ahora sabes cómo trasladar la geometría por todo el plano cartesiano y analizar sus ecuaciones generales.
Este tema es una pieza clave de nuestro artículo pilar sobre Geometría Analítica. Te recomendamos visitarlo para conectar este conocimiento con otras cónicas como la parábola o la hipérbola.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Selectos de matemáticas
★★★★★
-
Resolvió mi duda
★★★★★
10 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar