Ecuación de la Hipérbola con Centro en el Origen
La Hipérbola es, sin duda, la "hermana rebelde" de las cónicas. Si ya dominas la elipse, verás que la hipérbola tiene una estructura similar, pero con una diferencia fundamental: en lugar de sumar distancias, las restamos. En este artículo vamos a dominar la Ecuación de la Hipérbola con Centro en el Origen, cubriendo sus fórmulas, gráficas y ejercicios resueltos paso a paso.
Este tema es el broche de oro de la geometría analítica. Prepárate, porque vamos a desglosar todo lo que necesitas saber para aprobar tu examen y entender las gráficas a la perfección.
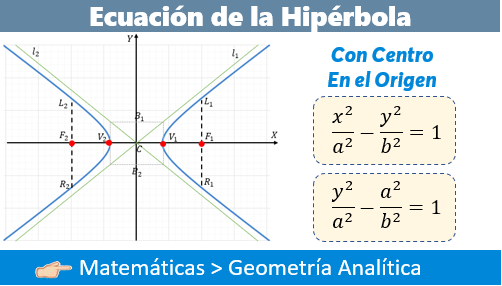
¿Qué es una Hipérbola?
Antes de pasar a los números, entendamos la definición formal. A diferencia de la elipse (que es una suma constante), la hipérbola funciona con una diferencia.
Definición de la Hipérbola
La Hipérbola es el lugar geométrico de los puntos del plano que se mueven de tal manera que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es siempre constante e igual a \(2a\).
Elementos de la Hipérbola con Centro en el Origen
Para resolver cualquier problema de hipérbolas, necesitas identificar a sus protagonistas. No importa si la hipérbola es horizontal o vertical, siempre tendremos estos elementos clave:
- Centro \(C(0,0)\): El punto donde se cruzan los ejes y donde "nace" nuestra figura.
- Focos \(F\): Puntos fijos dentro de las ramas de la hipérbola. La distancia del centro a un foco es \(c\).
- Vértices \(V\): Los puntos donde la hipérbola corta a su eje principal. La distancia del centro al vértice es \(a\).
- Eje Transverso (\(2a\)): Es el eje principal que une los dos vértices.
- Eje Conjugado (\(2b\)): Es el eje imaginario perpendicular al transverso.
- Asíntotas: Dos líneas rectas que la hipérbola intenta tocar pero nunca alcanza. Son vitales para graficar correctamente.
⚠️ ¡Cuidado con esta Fórmula!
En la hipérbola, la relación entre \(a\), \(b\) y \(c\) es diferente a la de la elipse. Aquí, el segmento más grande siempre es la distancia focal \(c\). Por lo tanto, el Teorema de Pitágoras se aplica así:
\[ c^2 = a^2 + b^2 \]
Recuerda siempre: \(c > a\) y \(c > b\).
Tipos de Hipérbolas: ¿Vertical u Horizontal?
Esta es la pregunta del millón y la clave para usar la fórmula correcta. En el examen, podrás distinguirlas fácilmente mirando cuál variable es positiva en la ecuación canónica.
1. Hipérbola Horizontal
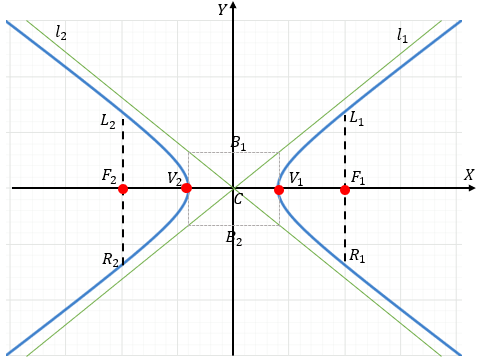
Sabemos que es horizontal cuando su eje focal coincide con el eje X. En la ecuación, identificarás esto porque el término \(x^2\) es positivo.
Ecuación Canónica:
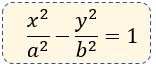
Elementos Clave:
- Vértices: \( V(\pm a, 0) \)
- Focos: \( F(\pm c, 0) \)
- Asíntotas: \( y = \pm \frac{b}{a}x \)
2. Hipérbola Vertical
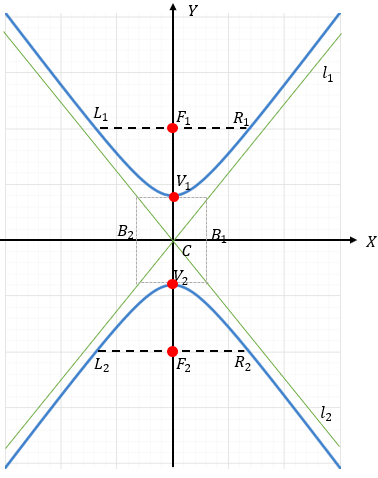
Es vertical cuando su eje focal coincide con el eje Y. Aquí, el término positivo es la \(y^2\), mientras que la \(x^2\) es negativa.
Ecuación Canónica:
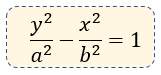
Elementos Clave:
- Vértices: \( V(0, \pm a) \)
- Focos: \( F(0, \pm c) \)
- Asíntotas: \( y = \pm \frac{a}{b}x \)
💡 Truco para las Asíntotas
No necesitas memorizar dos fórmulas de asíntotas. Simplemente despeja \(y\) de la ecuación de la hipérbola cuando esta está igualada a 0 en lugar de a 1. ¡Te dará la pendiente correcta automáticamente!
Ejercicios Resueltos de Hipérbola con Centro en el Origen
La mejor forma de aprender es practicando. Vamos a resolver ejercicios de hipérbola paso a paso, cubriendo tanto casos horizontales como verticales.
Ejemplo 1: Análisis de una Ecuación General
Determinar los elementos (vértices, focos, asíntotas) y trazar la gráfica de la hipérbola dada por la ecuación: \( 9x^2 - 4y^2 - 36 = 0 \).
Solución:
Paso 1: Transformar a la forma canónica.
Primero, movemos el término independiente al lado derecho:
\[ 9x^2 - 4y^2 = 36 \]
Ahora, dividimos toda la ecuación entre 36 para igualar a 1:
\[ \frac{9x^2}{36} - \frac{4y^2}{36} = \frac{36}{36} \]
Simplificamos las fracciones:
\[ \frac{x^2}{4} - \frac{y^2}{9} = 1 \]
Paso 2: Identificar el tipo de hipérbola.
Observa que el término \(x^2\) es positivo. Esto significa que estamos ante una Hipérbola Horizontal.
Paso 3: Obtener los parámetros \(a, b\) y \(c\).
De la ecuación \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), deducimos:
- \( a^2 = 4 \Rightarrow \mathbf{a = 2} \)
- \( b^2 = 9 \Rightarrow \mathbf{b = 3} \)
Para hallar \(c\) (distancia focal), usamos Pitágoras (\(c^2 = a^2 + b^2\)):
\[ c = \sqrt{4 + 9} = \sqrt{13} \approx 3.6 \]
Paso 4: Calcular los elementos.
- Vértices \(V(\pm a, 0)\): \( V_1(2, 0) \) y \( V_2(-2, 0) \)
- Focos \(F(\pm c, 0)\): \( F_1(\sqrt{13}, 0) \) y \( F_2(-\sqrt{13}, 0) \)
- Extremos conjugados \(B(0, \pm b)\): \( B_1(0, 3) \) y \( B_2(0, -3) \)
- Lado Recto: \( LR = \frac{2b^2}{a} = \frac{2(9)}{2} = \mathbf{9} \)
- Excentricidad: \( e = \frac{c}{a} = \frac{\sqrt{13}}{2} \approx 1.8 \)
Paso 5: Ecuaciones de las Asíntotas.
Para una hipérbola horizontal, la pendiente es \( m = \pm \frac{b}{a} \):
\[ y = \pm \frac{3}{2}x \]
Esto nos da dos rectas: \( 3x - 2y = 0 \) y \( 3x + 2y = 0 \).
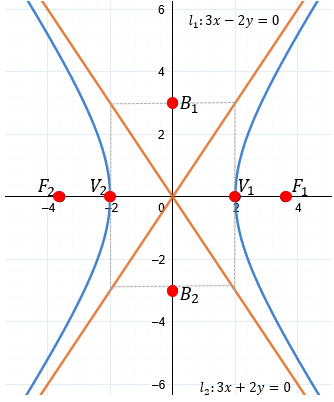
Gráfica:
Aquí podemos ver la representación gráfica con sus asíntotas:
Ejemplo 2: Hipérbola Vertical dada su ecuación
Encuentra las coordenadas de los vértices y focos de la hipérbola: \( 16y^2 - 9x^2 = 144 \).
Solución:
Paso 1: Forma canónica.
Dividimos todo entre 144:
\[ \frac{16y^2}{144} - \frac{9x^2}{144} = 1 \]
\[ \frac{y^2}{9} - \frac{x^2}{16} = 1 \]
Paso 2: Análisis.
Como el término \(y^2\) es positivo, es una Hipérbola Vertical.
Paso 3: Parámetros.
- \( a^2 = 9 \Rightarrow \mathbf{a = 3} \) (Recuerda: en la hipérbola, \(a^2\) es el denominador del término positivo).
- \( b^2 = 16 \Rightarrow \mathbf{b = 4} \)
- \( c = \sqrt{a^2 + b^2} = \sqrt{9 + 16} = \sqrt{25} \Rightarrow \mathbf{c = 5} \)
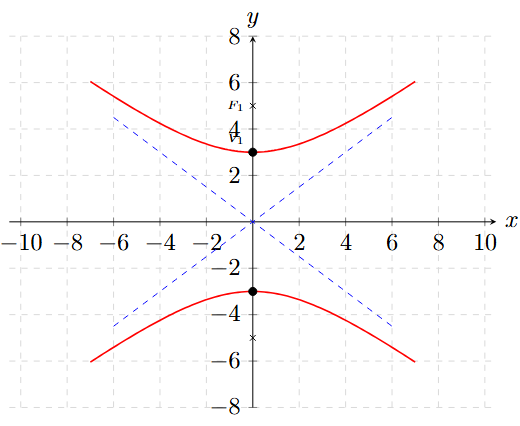
Paso 4: Elementos.
Al ser vertical, las coordenadas cambian en el eje Y:
- Vértices \(V(0, \pm a)\): \( V(0, 3) \) y \( V(0, -3) \)
- Focos \(F(0, \pm c)\): \( F(0, 5) \) y \( F(0, -5) \)
Ejemplo 3: Construir la ecuación
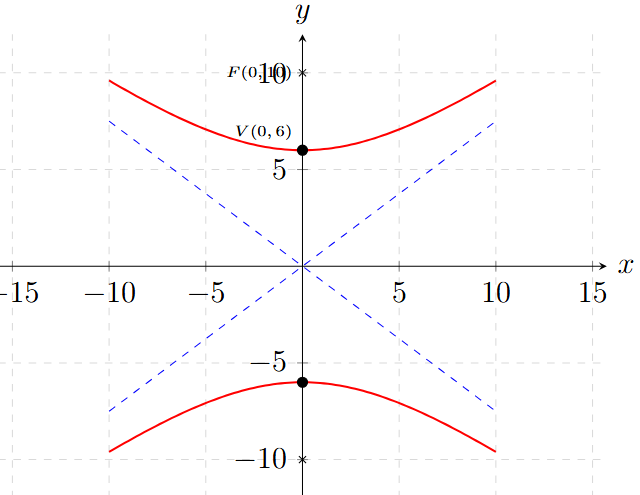
Halla la ecuación de la hipérbola con centro en el origen, un vértice en \( V(0, 6) \) y un foco en \( F(0, 10) \).
Solución:
Paso 1: Identificar orientación.
Como el vértice y el foco están en el eje Y (la coordenada x es 0), la hipérbola es Vertical.
Paso 2: Obtener \(a\), \(b\) y \(c\).
- Del vértice \(V(0, 6)\) sabemos que \( a = 6 \).
- Del foco \(F(0, 10)\) sabemos que \( c = 10 \).
- Necesitamos \(b\). Despejamos de Pitágoras: \( b^2 = c^2 - a^2 \).
\[ b^2 = 10^2 - 6^2 = 100 - 36 = 64 \]
\[ b = 8 \]
Paso 3: Sustituir en la fórmula.
Usamos la estructura vertical \(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\):
\[ \frac{y^2}{36} - \frac{x^2}{64} = 1 \]
Ejemplo 4: Hallar la ecuación dada la Excentricidad
Determina la ecuación de una hipérbola horizontal con centro en el origen, sabiendo que su eje transverso mide 12 unidades y su excentricidad es \( e = \frac{5}{3} \).
Solución:
Paso 1: Obtener \(a\) del eje transverso.
Sabemos que la longitud del eje transverso es \(2a\).
\[ 2a = 12 \Rightarrow a = 6 \]
Paso 2: Usar la excentricidad para hallar \(c\).
La fórmula de la excentricidad es \( e = \frac{c}{a} \). Sustituimos los valores conocidos:
\[ \frac{5}{3} = \frac{c}{6} \]
Despejamos \(c\):
\[ c = \frac{5 \cdot 6}{3} = \frac{30}{3} = 10 \]
Paso 3: Calcular \(b\) con Pitágoras.
Recordemos que \(c^2 = a^2 + b^2\), por lo tanto \( b^2 = c^2 - a^2 \):
\[ b^2 = 10^2 - 6^2 = 100 - 36 = 64 \]
Paso 4: Armar la ecuación.
Al ser una hipérbola horizontal (lo dice el enunciado), usamos la forma \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \):
\[ \frac{x^2}{36} - \frac{y^2}{64} = 1 \]
Ejemplo 5: Ecuación a partir de las Asíntotas
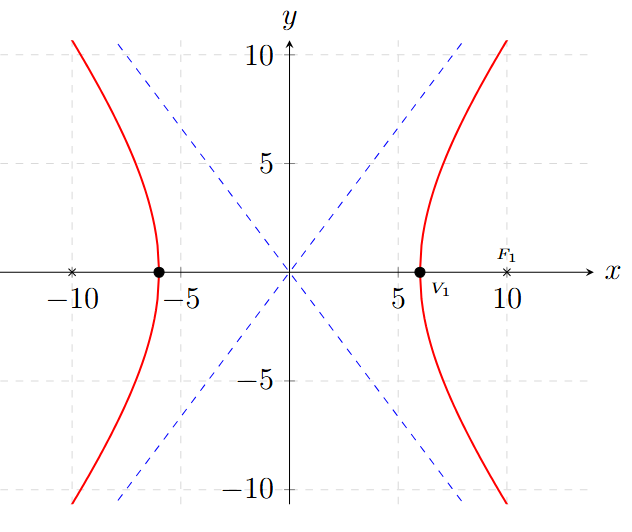
Halla la ecuación de la hipérbola vertical que tiene sus focos en \( F(0, \pm 10) \) y cuyas asíntotas son las rectas \( y = \pm \frac{4}{3}x \).
Solución:
Paso 1: Analizar los datos.
Al estar los focos en el eje Y \((0, \pm 10)\), confirmamos que es vertical y que \( c = 10 \).
Paso 2: Relacionar las asíntotas con \(a\) y \(b\).
Para una hipérbola vertical, la pendiente de la asíntota es \( m = \frac{a}{b} \).
Según el problema, \( \frac{a}{b} = \frac{4}{3} \). Esto no significa que \(a=4\) y \(b=3\) necesariamente, sino que están en esa proporción. Podemos decir que:
- \( a = 4k \)
- \( b = 3k \)
Paso 3: Hallar la constante \(k\).
Usamos la relación fundamental \( c^2 = a^2 + b^2 \):
\[ 10^2 = (4k)^2 + (3k)^2 \]
\[ 100 = 16k^2 + 9k^2 \]
\[ 100 = 25k^2 \]
\[ k^2 = \frac{100}{25} = 4 \Rightarrow k = 2 \]
Paso 4: Calcular valores reales de \(a\) y \(b\).
- \( a = 4(2) = 8 \Rightarrow a^2 = 64 \)
- \( b = 3(2) = 6 \Rightarrow b^2 = 36 \)
Paso 5: Ecuación Final.
Sustituimos en la forma vertical \( \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 \):
\[ \frac{y^2}{64} - \frac{x^2}{36} = 1 \]
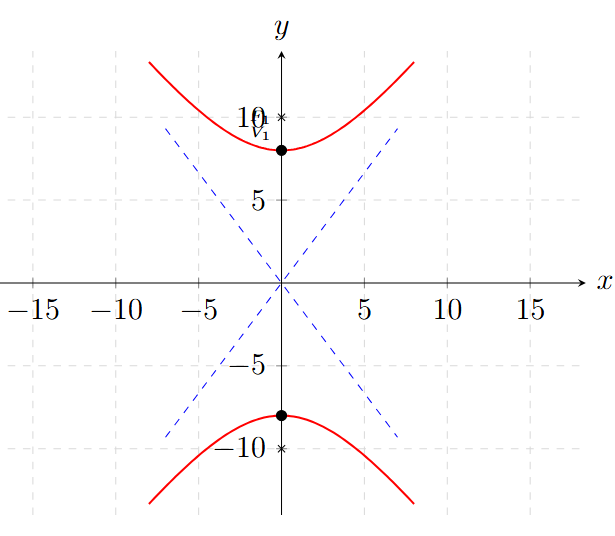
Ejemplo 6: Usando el Lado Recto
Encuentra la ecuación de la hipérbola con centro en el origen, eje focal sobre el eje X, un vértice en \( V(4,0) \) y longitud de su lado recto igual a 9.
Solución:
Paso 1: Identificar datos.
Eje focal sobre X = Horizontal.
Vértice en \( (4,0) \implies a = 4 \).
Lado Recto \( LR = 9 \).
Paso 2: Despejar \(b\) de la fórmula del Lado Recto.
Sabemos que \( LR = \frac{2b^2}{a} \). Sustituimos lo que tenemos:
\[ 9 = \frac{2b^2}{4} \]
Multiplicamos por 4 para eliminar el denominador:
\[ 36 = 2b^2 \]
\[ b^2 = \frac{36}{2} = 18 \]
Paso 3: Ecuación.
Tenemos \( a^2 = 4^2 = 16 \) y \( b^2 = 18 \).
La ecuación es:
\[ \frac{x^2}{16} - \frac{y^2}{18} = 1 \]
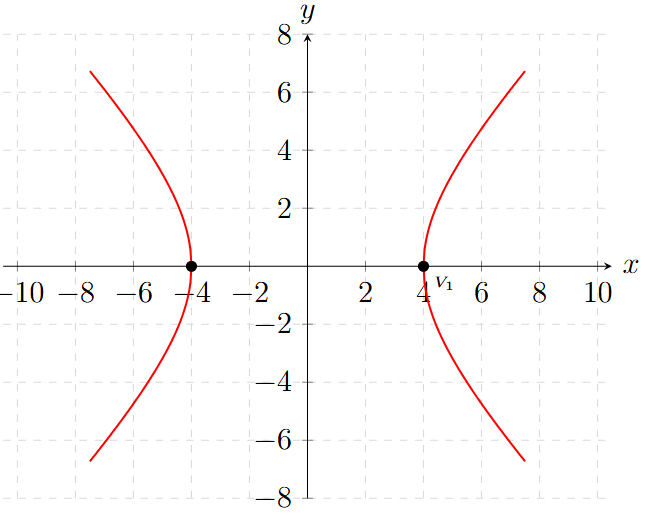
Ejemplo 7: Ecuación General a Canónica (Caso complejo)
Dada la ecuación general \( 4y^2 - x^2 + 64 = 0 \), transfórmala a su forma canónica y determina las coordenadas de los vértices.
Solución:
Paso 1: Reordenar la ecuación.
Este ejercicio tiene una "trampa" común. Primero, dejemos las variables a la izquierda y el número a la derecha:
\[ 4y^2 - x^2 = -64 \]
Paso 2: Buscar el 1 positivo a la derecha.
Para que sea canónica, debe estar igualada a 1 positivo. Dividimos todo entre -64:
\[ \frac{4y^2}{-64} - \frac{x^2}{-64} = \frac{-64}{-64} \]
Simplificamos los signos y fracciones:
\[ -\frac{y^2}{16} + \frac{x^2}{64} = 1 \]
Reordenamos para que el positivo quede primero:
\[ \frac{x^2}{64} - \frac{y^2}{16} = 1 \]
Paso 3: Interpretación.
¡Sorpresa! Aunque al inicio la \(y\) parecía positiva, al despejar el término independiente, la ecuación resultante tiene a \(x^2\) positiva. Es una Hipérbola Horizontal.
- \( a^2 = 64 \Rightarrow a = 8 \)
- \( b^2 = 16 \Rightarrow b = 4 \)
Paso 4: Vértices.
Al ser horizontal, los vértices están en \( V(\pm a, 0) \):
\[ V_1(8, 0) \text{ y } V_2(-8, 0) \]
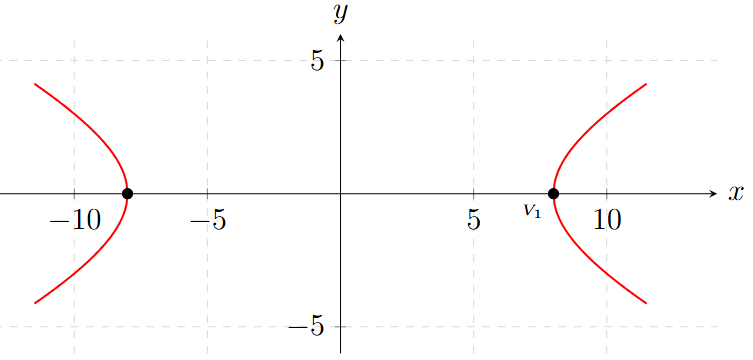
Problemas Propuestos para Practicar
¿Listo para poner a prueba lo aprendido? Resuelve los siguientes ejercicios de hipérbola.
Problema Propuesto 1
Dada la hipérbola \( 25x^2 - 144y^2 = 3600 \), encuentra las coordenadas de sus focos.
Haz clic aquí para ver la solución
1. Dividimos entre 3600: \( \frac{x^2}{144} - \frac{y^2}{25} = 1 \).
2. Es Horizontal (\(x\) positiva).
3. \( a^2 = 144 \), \( b^2 = 25 \).
4. Calculamos \( c \): \( c = \sqrt{144 + 25} = \sqrt{169} = 13 \).
Respuesta: Los focos están en \( F(\pm 13, 0) \).
Problema Propuesto 2
Encuentra la ecuación de la hipérbola horizontal con centro en el origen, eje transverso de longitud 8 y eje conjugado de longitud 6.
Haz clic aquí para ver la solución
1. Eje Transverso \( 2a = 8 \Rightarrow a = 4 \Rightarrow a^2 = 16 \).
2. Eje Conjugado \( 2b = 6 \Rightarrow b = 3 \Rightarrow b^2 = 9 \).
3. Al ser horizontal, la fórmula es \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \).
Respuesta: \( \frac{x^2}{16} - \frac{y^2}{9} = 1 \).
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado la Hipérbola con Centro en el Origen. Ahora eres capaz de distinguir entre verticales y horizontales y calcular todos sus elementos.
Pero el viaje no termina aquí. La geometría analítica es vasta y fascinante. Para conectar este tema con las demás cónicas y tener una visión completa, visita nuestro artículo pilar sobre Geometría Analítica.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
me ayudo mucho, pero no se si se equivoco en el ejercicio por que no seria hipérbola horizontal, por que cuando ya la grafico lo pone en horizontal y decía que era en vertical y en la ecuación es x-y= 1 lo cual es la ecuación canónica de la hipérbola horizontal esa es mi duda o no se si me pueda explicar en eso muchas gracias aun así me ayudo
-
Me ayudó muchísimo, pero tiene algunos errores y me gustaría si pudiera usted corregirlos para que los demás estudiantes como yo no se confundan. Gracias por su trabajo.
-
Se que sonará estúpido, pero, ¿Cómo identifico si una hipérbola es vertical u horizontal?
-
primero si se trata de una ecuación general tienes que convertirla a canónica, una vez hecho esto tienes que ver cual es el valor de a, el cual es el valor del denominador de la fracción positiva, la fracción de negativa es b, luego que ya observaste cual es la fracción positiva mira si en el denominador esta la X, entonces es una hipérbola horizontal, pero si esta la Y es vertical.
-
6 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar