Ley de Coulomb - Ejercicios Resueltos
Antes de comenzar a platicar sobre la ley de Coulomb, ¿sabías que las fuerzas invisibles entre partículas cargadas son responsables de muchos de los fenómenos que observamos a diario, desde el funcionamiento de nuestros dispositivos electrónicos hasta los relámpagos en una tormenta?. La ley de Coulomb nos permite entender cómo las cargas eléctricas interactúan, ya sea atrayéndose o repeliéndose, dependiendo de su naturaleza.
En este artículo, exploraremos los principios que gobiernan estas interacciones, analizaremos casos prácticos de atracción y repulsión entre cargas, y resolveremos ejercicios que te ayudarán a dominar este fascinante tema. Este es uno de los temas que más nos han pedido en la página de física.
¿Quién fue Charles Coulomb?
Antes de hablar sobre su ley, hagamos una pequeña síntesis sobre quien fue el gran Coulomb. Charles Coulomb fue un científico francés que estudió las leyes tanto de atracción como repulsión de dos cargas eléctricas puntuales sobre el reposo.
De ahí postuló, que cuando mayor es la distancia entre dos cuerpos cargados eléctricamente, menor será la magnitud de fuerza que haya de atracción o repulsión .
La ley de coulomb, nos dice lo siguiente:
Suena algo confuso ¿cierto?, la cuestión es entenderlo, por ahora no te preocupes sino entendiste lo del enunciado, esto en términos matemáticos se expresa de la siguiente manera:
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
dónde:
$\displaystyle {{q}_{1}},{{q}_{2}}$ = Cargas eléctricas [Coulomb]
$\displaystyle F$ = Fuerza [Newton]
$\displaystyle d$ = Distancia [Metros]
$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$ = Constante de Coulomb
Gráficamente lo podemos ver de la siguiente forma:
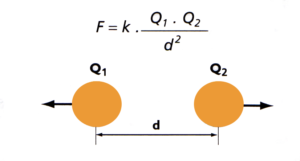
Esto quiere decir, que podemos saber la fuerza de atracción o repulsión de las cargas eléctricas, respecto a la distancia a la que estén separadas, o alejadas. Esto es fácil de entender, y si te has dado cuenta, es similar a ley de la gravitación universal. Por lo que podemos deducir que:
Ahora veamos los ejercicios resueltos de la ley de coulomb.
✅ Ejercicios Resueltos de la Ley de Coulomb
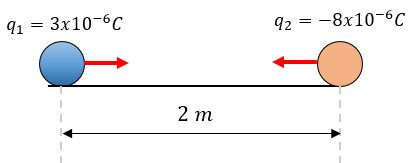
Solución: Para darle solución al ejercicio, debemos de obtener los datos para poder resolverlo de manera directa, puesto que tenemos todo lo que necesitamos.
$\displaystyle {{q}_{1}}=3x{{10}^{-6}}C$
$\displaystyle {{q}_{2}}=-8x{{10}^{-6}}C$
$l\displaystyle d=2m$
$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
Aplicando la fórmula de la ley de coulomb
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
Sustituimos
$\displaystyle F=\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right]\frac{(3x{{10}^{-6}}C)\cdot (-8x{{10}^{-6}}C)}{{{(2m)}^{2}}}$
$\displaystyle F=\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right]\frac{-24x{{10}^{-12}}{{C}^{2}}}{4{{m}^{2}}}$
Hemos multiplicado las cargas eléctricas, recordar que los exponentes se suman. y hemos elevado al cuadrado la distancia que los separa, ahora seguimos con las operaciones.
$\displaystyle F=\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right]-6x{{10}^{-12}}\frac{{{C}^{2}}}{{{m}^{2}}}$
Multiplicamos y obtenemos:
$\displaystyle F=-54x{{10}^{-3}}N=-0.054N$
Vemos que hay un signo negativo, por ahora no nos sirve interpretar el signo, puesto que el problema nos pide la magnitud de la fuerza, esto quiere decir que tomaremos la fuerza como un valor absoluto, que vendría a ser nuestro resultado.
$\displaystyle F=0.054N$
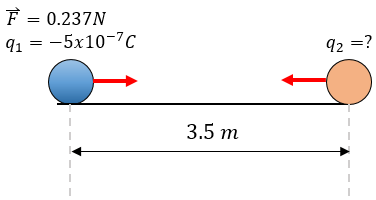
Solución: En este caso, tenemos una incógnita diferente al primer ejercicio, puesto que ahora nos piden hallar el valor de la segunda carga, esto lo haremos despejando en nuestra fórmula, asumiendo lo siguiente:
$\displaystyle {{q}_{1}}=-5x{{10}^{-7}}C$
$\displaystyle F=0.237N$
$\displaystyle d=3.5m$
$\displaystyle {{q}_{2}}=$ ?
Despejaremos la primera fórmula, para obtener $\displaystyle {{q}_{2}}$
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
$\displaystyle F\cdot {{d}^{2}}=K\cdot {{q}_{1}}\cdot {{q}_{2}}$
$\displaystyle {{q}_{2}}=\frac{F\cdot {{d}^{2}}}{K\cdot {{q}_{1}}}$
Ahora vamos a sustituir nuestros datos
$\displaystyle {{q}_{2}}=\frac{(0.237N){{(3.5m)}^{2}}}{\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right]\cdot -5x{{10}^{-7}}C}$
$\displaystyle {{q}_{2}}=\frac{2.90N{{m}^{2}}}{\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right]\cdot -5x{{10}^{-7}}C}$
$\displaystyle {{q}_{2}}=\frac{2.90N{{m}^{2}}}{-4500\frac{N{{m}^{2}}}{C}}$
$\displaystyle {{q}_{2}}=-0.644x{{10}^{-3}}C$
Que sería el valor de la segunda carga, para poder cumplir con los datos propuestos por el problema.
Veamos ahora otro ejemplo, en este caso nuestra incógnita será la distancia.

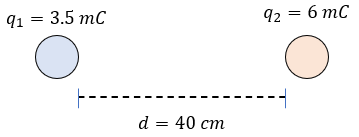
Solución: El problema es sencillo de resolver, ahora veamos los datos que tenemos:
$\displaystyle {{q}_{1}}=2.8x{{10}^{-6}}C$
$\displaystyle {{q}_{2}}=7.5x{{10}^{-6}}C$
$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
$\displaystyle d=$ ?
Ahora tendremos que despejar, nuevamente la fórmula de la ley de coulumb.
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
$\displaystyle {{d}^{2}}=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{F}$
$\displaystyle d=\sqrt{\frac{K\cdot {{q}_{1}}\cdot {{q}_{2}}}{F}}$
Ahora tenemos que sustituir nuestros datos
$\displaystyle d=\sqrt{\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)(2.8x{{10}^{-6}}C)(7.5x{{10}^{-6}}C)}{10N}}$
$\displaystyle d=\sqrt{\frac{0.189N{{m}^{2}}}{10N}}=\sqrt{0.0189{{m}^{2}}}=0.1374m$
Por lo que nuestro resultado es de .1374 metros de distancia entre las cargas, para un efecto de 10 Newtons.
Solución:
Veamos este problema similar a uno de los ejercicios anteriores, pero nos ayudará a reforzar nuestra comprensión de esta ley.
Datos proporcionados:
$\displaystyle {{q}_{1}}=5.0x{{10}^{-6}}C$
$\displaystyle {{q}_{2}}=3.0x{{10}^{-6}}C$
$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
$\displaystyle F=15N$
$\displaystyle d=$ ?
Despejamos $d$ de la Ley de Coulomb:
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
$\displaystyle {{d}^{2}}=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{F}$
$\displaystyle d=\sqrt{\frac{K\cdot {{q}_{1}}\cdot {{q}_{2}}}{F}}$
Sustitución:
$\displaystyle d=\sqrt{\frac{\left(9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}\right)(5.0x{{10}^{-6}}C)(3.0x{{10}^{-6}}C)}{15N}}$
Resultado numérico:
$\displaystyle d=\sqrt{\frac{0.135N{{m}^{2}}}{15N}} = \sqrt{0.009{{m}^{2}}} = 0.0949m$
Resultado: 0.0949 metros
Solución:
Datos:
$\displaystyle F=7N$
$\displaystyle {{q}_{2}}=3.5x{{10}^{-6}}C$
$\displaystyle d=0.2m$
$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
$\displaystyle {{q}_{1}}=$ ?
Despeje de $q_1$:
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
$\displaystyle {{q}_{1}}= \frac{F \cdot {{d}^{2}}}{K \cdot {{q}_{2}}}$
Sustitución:
$\displaystyle {{q}_{1}}= \frac{(7N)(0.2m)^2}{(9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}})(3.5x{{10}^{-6}}C)}$
$\displaystyle {{q}_{1}}= \frac{0.28N{{m}^{2}}}{3.15x{{10}^{4}}N{{m}^{2}}/C} = 8.888x{{10}^{-6}}C$
$\displaystyle {{q}_{1}} = 8.89 \times 10^{-6}\, \text{C}$.
Por lo tanto el resultado de q1 = 8.89 x 10^(-6) C
Solución:
Datos:
$\displaystyle F=10N$
$\displaystyle {{q}_{1}}=8x{{10}^{-6}}C$
$\displaystyle d=0.15m$
$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
$\displaystyle {{q}_{2}}=$ ?
Despeje de $q_2$:
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
$\displaystyle {{q}_{2}}= \frac{F \cdot {{d}^{2}}}{K \cdot {{q}_{1}}}$
Sustitución:
$\displaystyle {{q}_{2}}= \frac{(10N)(0.15m)^2}{(9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}})(8x{{10}^{-6}}C)}$
$\displaystyle {{q}_{2}}= \frac{0.225N{{m}^{2}}}{0.072N{{m}^{2}}/C} = 3.125x{{10}^{-6}}C$
$\displaystyle {{q}_{2}} = 3.13 \times 10^{-6}\, \text{C}$.
Por lo tanto el resultado es de 3.13 x 10^(-6) C
Solución:
Datos:
$\displaystyle F=9N$
$\displaystyle {{q}_{1}}=2x{{10}^{-6}}C$
$\displaystyle {{q}_{2}}=5x{{10}^{-6}}C$
$\displaystyle d=0.1m$
$\displaystyle K=$ ?
Despeje de $K$:
$\displaystyle F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
$\displaystyle K= \frac{F \cdot {{d}^{2}}}{{{q}_{1}}\cdot {{q}_{2}}}$
Sustitución:
$\displaystyle K= \frac{(9N)(0.1m)^2}{(2x{{10}^{-6}}C)(5x{{10}^{-6}}C)}$
$\displaystyle K= \frac{0.09N{{m}^{2}}}{1x{{10}^{-11}}C^2} = 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
$\displaystyle K = 9 \times 10^9\, \frac{\text{N·m}^2}{\text{C}^2}$ (se verifica correctamente).
Como se puede observar se comprueba en este ejercicio el valor de K = 9x10^9 Nm^2/C^2
Ejercicios Para Practicar
Genial, ahora es momento de practicar, y analizar si realmente hemos comprendido los problemas resueltos de la Ley de Coulomb.
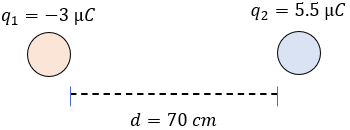
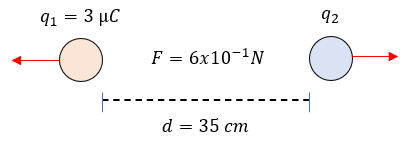
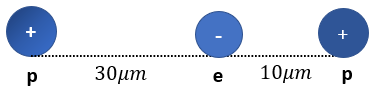
Resuelve el Examen de la Ley de Coulomb
Llegó el momento de que pongas a pruebas tus conocimientos de la Ley de Coulomb. ¿Podrás lograr obtener todas buenas? 🚀💛
Cargando examen...
Ejercicios Resueltos en PDF de la Ley de Coulomb
He preparado esta guía completa con todos los ejercicios resueltos paso a paso. Es perfecta para que la guardes, la imprimas y la uses para estudiar en cualquier lugar, incluso sin conexión a internet. ¡Ideal para repasar antes de tu examen!
✨ Conclusión
La Ecuación de Coulomb, solamente es válida cuando las cargas se encuentra en el vacío, o hay una aproximación muy cercana al aire, puesto que la permitividad relativa es próxima al vacío. 😀
Como te podrás dar cuenta, no es difícil, simplemente debemos establecer nuestros datos y resolver... Si tienes problemas de despeje, qué es lo más común, hemos ya publicado en el blog un artículo sobre como despejar fórmulas. Así no tendrás ese tipo de situaciones incómodas y no poder llegar al resultado.
Ahora la Ley de Coulomb no solo se define para dos cargas, sino que éstas pueden ser más de dos y el problema se acompleja , ahí es donde subimos un poco el nivel, a dicho tema se le conoce como el principio de superposición, de hecho tenemos ya algunos ejemplos resueltos. 😀
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Excelente los ejercicios
★★★★★
-
dos cargas q1=5 uC y q2 =-3uC estan separadas por una distancia de 0.4m0.4, m0.4m. utiliza la formula de la ley de coulomb para calcular la magnitud de la fuerza q actúa entre ellas ¿es una fuerza de atracción o repulsión ?
-
según yo es atracción
★★★★★
-
-
Cuál debe ser la distancia de separación entre dos cargas de 4 * 10^- 5 C cada una para la fuerza de repulsión entre ellas tenga un módulo de 160N
-
emm..por que a mi me da 2.45x10-17 en la actividad 6? 🙁
700 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar