Ecuación de la Circunferencia con Centro fuera del Origen
Cuando iniciamos el estudio de la Geometría Analítica, es común empezar por lo más sencillo: la circunferencia centrada en el origen \( (0,0) \). Sin embargo, en la vida real y en los exámenes de ingeniería, las figuras geométricas rara vez están tan bien portadas. A menudo, se desplazan.
Hoy vamos a dominar el caso más frecuente y útil: la ecuación de la circunferencia con centro fuera del origen. No te preocupes, la lógica es idéntica a la que ya conoces, solo añadiremos un par de coordenadas nuevas: \( h \) y \( k \).
Lo que aprenderás en este artículo
- La diferencia entre la Forma Ordinaria y la Forma General.
- Las fórmulas exactas para no equivocarte con los signos.
- Resolución de ejercicios paso a paso (desde encontrar la ecuación hasta graficar).
- Cómo obtener el radio y el centro a partir de una ecuación general.
¿Cuál es la Ecuación de la Circunferencia fuera del Origen?
Para entender este concepto, debemos recordar que una circunferencia es el lugar geométrico de todos los puntos \( P(x, y) \) que equidistan de un punto fijo llamado centro. Cuando este centro no está en el origen, sus coordenadas se denotan como \( C(h, k) \).
Para representar esto matemáticamente, utilizamos la Forma Ordinaria (también conocida como canónica en algunos textos, aunque la distinción estricta suele reservar "canónica" para el origen).
Fórmula: Forma Ordinaria de la Circunferencia
Si una circunferencia tiene su centro en el punto \( C(h, k) \) y un radio \( r \), su ecuación está dada por:
\[ (x - h)^2 + (y - k)^2 = r^2 \]
Esta fórmula nace directamente del Teorema de Pitágoras y la fórmula de distancia entre dos puntos. Observa la siguiente imagen que ilustra cómo los catetos se forman por las diferencias \( (x-h) \) y \( (y-k) \):
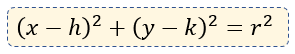
Gráficamente, esto significa que la circunferencia se ha "trasladado" del centro del plano cartesiano a una nueva posición:
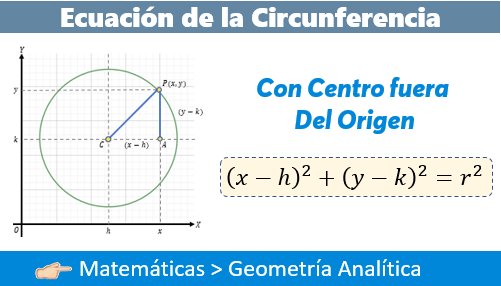
⚠️ Cuidado con los signos
El error más común en los exámenes es olvidar que la fórmula tiene signos negativos por defecto: \( (x - h) \).
- Si el centro es \( (2, 3) \), en la fórmula pondrás \( (x - 2) \) y \( (y - 3) \).
- Si el centro tiene coordenadas negativas, como \( (-2, -3) \), la fórmula cambiará los signos: \( (x - (-2)) \) se convierte en \( (x + 2) \).
Diferencia entre Ecuación Ordinaria y Ecuación General
A menudo te pedirán expresar el resultado de dos formas distintas. Es vital que sepas distinguirlas:
- Ecuación Ordinaria: Es la forma \( (x-h)^2 + (y-k)^2 = r^2 \). Es muy útil porque nos deja ver "a simple vista" las coordenadas del centro y el valor del radio.
- Ecuación General: Se obtiene al desarrollar los binomios al cuadrado de la ordinaria e igualar a cero. Tiene la forma:
\[ Ax^2 + Cy^2 + Dx + Ey + F = 0 \]
Donde \( A \) y \( C \) deben ser iguales para que sea una circunferencia.
Ejercicios Resueltos de Circunferencia con Centro Fuera del Origen
La mejor forma de aprender física y matemáticas es practicando. Vamos a resolver 4 ejemplos que cubren las variantes más buscadas en los exámenes: desde sustituir datos hasta completar trinomios cuadrados perfectos.
Ejemplo 1: Obtener la ecuación ordinaria dados el Centro y Radio
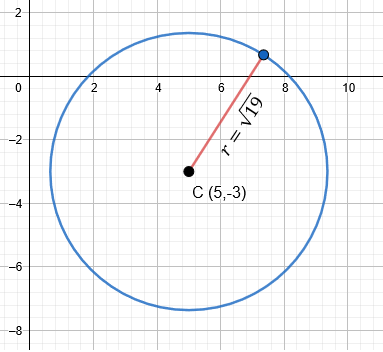
Determinar la ecuación de la circunferencia cuyo centro es el punto \( C(5, -3) \) y su radio es de \( \sqrt{19} \).
Solución:
Este es el caso más directo. Identificamos nuestros datos:
- \( h = 5 \)
- \( k = -3 \)
- \( r = \sqrt{19} \)
Sustituimos en la fórmula ordinaria \( (x-h)^2 + (y-k)^2 = r^2 \):
\[ (x - 5)^2 + (y - (-3))^2 = (\sqrt{19})^2 \]
Simplificamos los signos (menos por menos da más) y elevamos la raíz al cuadrado (la raíz se cancela con la potencia):
Resultado:
\[ (x - 5)^2 + (y + 3)^2 = 19 \]
La gráfica de este ejercicio se vería así:
Ejemplo 2: De la forma ordinaria a la Ecuación General
Encuentra la ecuación general de la circunferencia con centro en \( (2, -1) \) y radio \( 6 \).
Solución:
Aquí daremos un paso extra. Primero armamos la ecuación ordinaria y luego desarrollamos el álgebra.
Datos: \( h=2 \), \( k=-1 \), \( r=6 \).
Sustituimos:
\[ (x - 2)^2 + (y - (-1))^2 = 6^2 \]
\[ (x - 2)^2 + (y + 1)^2 = 36 \]
Para llegar a la Ecuación General, desarrollamos los binomios al cuadrado \( (a \pm b)^2 = a^2 \pm 2ab + b^2 \):
\[ (x^2 - 4x + 4) + (y^2 + 2y + 1) = 36 \]
Ordenamos los términos (primero los cuadrados, luego los lineales, luego las constantes) e igualamos a cero pasando el 36 restando:
\[ x^2 + y^2 - 4x + 2y + 4 + 1 - 36 = 0 \]
Simplificamos los números (\( 4 + 1 - 36 = -31 \)):
Resultado:
\[ x^2 + y^2 - 4x + 2y - 31 = 0 \]
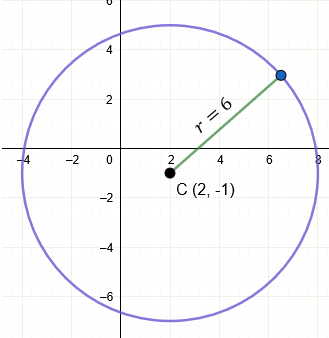
Ejemplo 3: Hallar la ecuación dado el Centro y un punto de paso
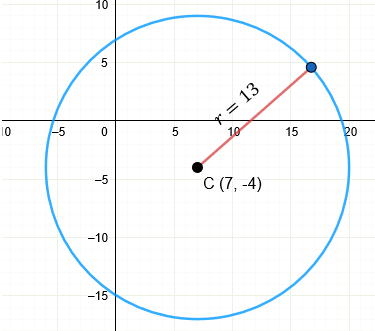
Determine la ecuación general de la circunferencia, si el centro está en las coordenadas \( C(7, -4) \) y dicha circunferencia pasa por el punto \( P(-5, 1) \).
Solución:
No nos dan el radio explícitamente, pero nos dan una pista clave: la distancia del Centro al punto \( P \) es el radio. Usaremos la fórmula de distancia entre dos puntos:
\[ r = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Sustituimos \( C(7, -4) \) como punto 1 y \( P(-5, 1) \) como punto 2:
\[ r = \sqrt{(-5 - 7)^2 + (1 - (-4))^2} \]
\[ r = \sqrt{(-12)^2 + (5)^2} \]
\[ r = \sqrt{144 + 25} = \sqrt{169} = 13 \]
Ahora que sabemos que \( r=13 \) y el centro es \( (7, -4) \), armamos la ecuación ordinaria:
\[ (x - 7)^2 + (y + 4)^2 = 13^2 \]
\[ (x - 7)^2 + (y + 4)^2 = 169 \]
Desarrollamos los binomios para obtener la general:
\[ x^2 - 14x + 49 + y^2 + 8y + 16 - 169 = 0 \]
Agrupamos y simplificamos:
\[ x^2 + y^2 - 14x + 8y + (49 + 16 - 169) = 0 \]
Resultado:
\[ x^2 + y^2 - 14x + 8y - 104 = 0 \]
Ejemplo 4: De la General a la Ordinaria (Completando Cuadrados)
Dada la ecuación general \( x^2 + y^2 + 6x - 8y - 11 = 0 \), determina las coordenadas del centro y el valor del radio.
Solución:
Este es un ejercicio clásico de examen que requiere "ingeniería inversa". Debemos agrupar las \( x \) y las \( y \) para completar el Trinomio Cuadrado Perfecto (TCP).
Paso 1: Agrupamos términos y pasamos la constante al otro lado.
\[ (x^2 + 6x) + (y^2 - 8y) = 11 \]
Paso 2: Completamos los cuadrados. La regla es: toma el coeficiente lineal (el número junto a la x o y), divídelo entre 2 y elévalo al cuadrado. Suma ese número a ambos lados de la ecuación.
- Para x: \( (6/2)^2 = 3^2 = 9 \)
- Para y: \( (-8/2)^2 = (-4)^2 = 16 \)
Agregamos estos números:
\[ (x^2 + 6x + \mathbf{9}) + (y^2 - 8y + \mathbf{16}) = 11 + \mathbf{9} + \mathbf{16} \]
Paso 3: Factorizamos los trinomios y sumamos la derecha.
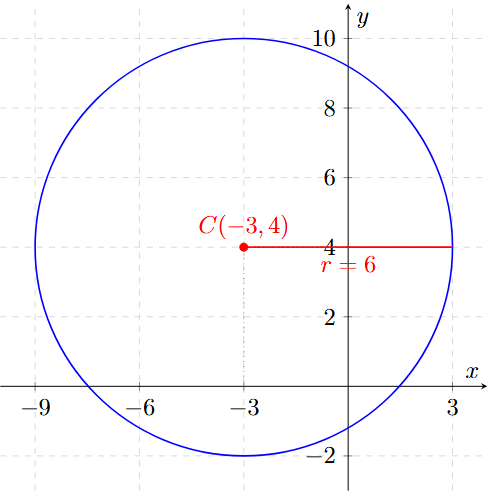
\[ (x + 3)^2 + (y - 4)^2 = 36 \]
Ahora comparamos con la forma \( (x-h)^2 + (y-k)^2 = r^2 \):
- \( -h = 3 \Rightarrow h = -3 \)
- \( -k = -4 \Rightarrow k = 4 \)
- \( r^2 = 36 \Rightarrow r = \sqrt{36} = 6 \)
Resultado:
Centro: \( C(-3, 4) \)
Radio: \( r = 6 \)
Ejemplo 5: Ecuación General con Coeficientes distintos de 1
Determina el centro y radio de la circunferencia dada por la ecuación: \( 4x^2 + 4y^2 - 16x + 24y - 12 = 0 \).
Solución:
¡Mucho cuidado aquí! Si observas bien, los términos cuadráticos tienen un coeficiente de 4. Para poder completar el Trinomio Cuadrado Perfecto y usar el método del ejemplo anterior, la x² y la y² deben estar solas.
Paso 1: Dividimos toda la ecuación entre 4 para simplificarla.
\[ \frac{4x^2}{4} + \frac{4y^2}{4} - \frac{16x}{4} + \frac{24y}{4} - \frac{12}{4} = \frac{0}{4} \]
Obtenemos una ecuación más amigable:
\[ x^2 + y^2 - 4x + 6y - 3 = 0 \]
Paso 2: Agrupamos las variables y pasamos la constante al lado derecho.
\[ (x^2 - 4x) + (y^2 + 6y) = 3 \]
Paso 3: Completamos los cuadrados.
- Para x: \( (-4/2)^2 = (-2)^2 = 4 \)
- Para y: \( (6/2)^2 = (3)^2 = 9 \)
Sumamos estos valores a ambos lados:
\[ (x^2 - 4x + \mathbf{4}) + (y^2 + 6y + \mathbf{9}) = 3 + \mathbf{4} + \mathbf{9} \]
Paso 4: Factorizamos.
\[ (x - 2)^2 + (y + 3)^2 = 16 \]
Ahora es fácil identificar los elementos:
Resultado:
Centro: \( C(2, -3) \)
Radio: \( r = \sqrt{16} = 4 \)

Ejemplo 6: Ecuación dados los extremos de un diámetro
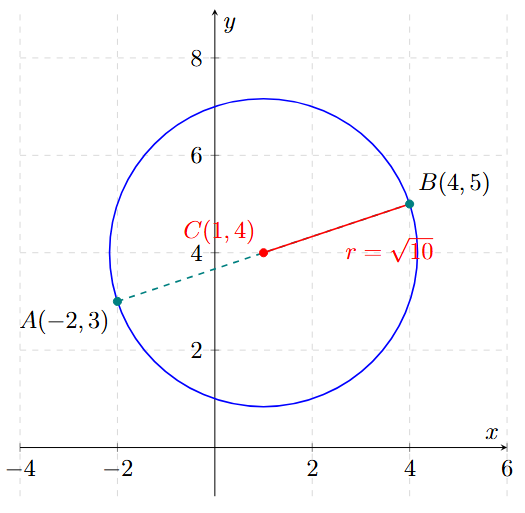
Halla la ecuación ordinaria de la circunferencia que tiene un diámetro con extremos en los puntos \( A(-2, 3) \) y \( B(4, 5) \).
Solución:
Este es un problema de razonamiento geométrico. No nos dan el centro ni el radio, pero nos dan el diámetro. Sabemos dos cosas fundamentales:
- El Centro es el punto medio del diámetro.
- El Radio es la distancia del centro a cualquiera de los extremos.
Paso 1: Calcular el Centro \( C(h,k) \) usando la fórmula del punto medio.
\[ h = \frac{x_1 + x_2}{2} = \frac{-2 + 4}{2} = \frac{2}{2} = 1 \]
\[ k = \frac{y_1 + y_2}{2} = \frac{3 + 5}{2} = \frac{8}{2} = 4 \]
Nuestro centro es \( C(1, 4) \).
Paso 2: Calcular el radio (distancia de C a B, por ejemplo).
\[ r = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
\[ r = \sqrt{(4 - 1)^2 + (5 - 4)^2} \]
\[ r = \sqrt{(3)^2 + (1)^2} = \sqrt{9+1} = \sqrt{10} \]
Paso 3: Sustituir en la ecuación ordinaria.
\[ (x - 1)^2 + (y - 4)^2 = (\sqrt{10})^2 \]
Resultado:
\[ (x - 1)^2 + (y - 4)^2 = 10 \]
Ejemplo 7: Circunferencia Tangente a los Ejes
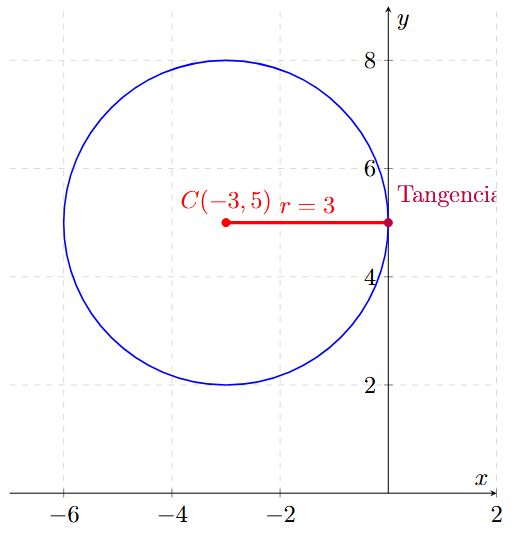
Encuentra la ecuación de la circunferencia con centro en \( C(-3, 5) \) y que es tangente al eje Y.
Solución:
A veces los problemas te dan el radio "escondido" en el enunciado. Si dibujas un plano cartesiano y ubicas el centro en \( (-3, 5) \), verás que para que el círculo "toque" (sea tangente) al eje Y, la distancia desde el centro hasta el eje debe ser exactamente igual al radio.
💡 Tip para Tangencias
- Si es tangente al Eje Y: El radio es el valor absoluto de la coordenada x del centro (\( r = |h| \)).
- Si es tangente al Eje X: El radio es el valor absoluto de la coordenada y del centro (\( r = |k| \)).
Aplicando esto a nuestro caso (tangente a Y):
\[ r = |-3| = 3 \]
Teniendo el centro \( C(-3, 5) \) y el radio \( r = 3 \), sustituimos:
\[ (x - (-3))^2 + (y - 5)^2 = 3^2 \]
Resultado:
\[ (x + 3)^2 + (y - 5)^2 = 9 \]
Ejercicios para Practicar
¡Es tu turno! Demuestra que eres un experto en la ecuación de la circunferencia resolviendo estos problemas propuestos.
Problema Propuesto 1
Encuentra la ecuación ordinaria de una circunferencia que tiene su centro en \( C(-4, 2) \) y un radio de \( 5 \).
Haz clic aquí para ver la solución
Datos: \( h=-4, k=2, r=5 \)
Sustitución:
\[ (x - (-4))^2 + (y - 2)^2 = 5^2 \]
Resultado:
\[ (x + 4)^2 + (y - 2)^2 = 25 \]
Problema Propuesto 2
Determina el centro y el radio de la circunferencia dada por la ecuación:
\[ (x - 1)^2 + (y + 5)^2 = 49 \]
Haz clic aquí para ver la solución
Comparamos directamente con la fórmula ordinaria.
- \( -h = -1 \Rightarrow h = 1 \)
- \( -k = 5 \Rightarrow k = -5 \)
- \( r^2 = 49 \Rightarrow r = 7 \)
Resultado:
Centro \( C(1, -5) \) y Radio \( r=7 \).
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado la Ecuación de la Circunferencia con Centro Fuera del Origen.
Este tema es una pieza clave de nuestro artículo pilar sobre Geometría Analítica. Te recomendamos visitarlo para ver cómo este conocimiento se conecta con la Parábola, la Elipse y la Hipérbola.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
x^2+y^2=36
-
ayúdeme:
Su centro es el origen y tiene radio 15/2 -
ayúdeme:
Su centro es el origen y tiene radio 6
3 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar