Caída Libre: Fórmulas y 20 Ejercicios Resueltos [PDF]
Hoy voy a tocar un tema que desafía nuestra intuición: ¿Por qué una pluma y un martillo caen a diferente velocidad en la Tierra pero igual en la Luna? La caída libre es el movimiento más puro de la naturaleza, gobernado únicamente por la gravedad.
¿Qué aprenderás hoy?
En esta guía dominarás:
- Las Fórmulas de Caída Libre (Altura, Tiempo y Velocidad).
- La diferencia entre lo que decía Aristóteles y Galileo.
- 10 Ejercicios Resueltos paso a paso (Desde edificios en CDMX hasta balones de fútbol).
- Acceso a nuestro PDF con 50 Ejercicios para descargar.
¿Qué es la Caída Libre?
Se dice que un cuerpo experimenta una caída libre cuando desciende sobre la superficie de la Tierra y no sufre ninguna resistencia originada por el aire. De manera práctica, en física de preparatoria despreciamos la fricción del aire.
Definición de Caída Libre
Es un movimiento uniformemente acelerado (MUA) donde la aceleración es la gravedad de la Tierra. Un dato clave: La velocidad inicial ($v_0$) generalmente es cero (se deja caer).
Aristóteles vs Galileo: El Gran Debate
Durante siglos, el mundo creyó a Aristóteles, quien decía que los objetos pesados caían más rápido que los ligeros. Tuvo que llegar un genio a cambiarlo todo.
Galileo Galilei
1564-1642
Considerado el padre del método experimental. Demostró que, en ausencia de aire, todos los cuerpos caen con la misma aceleración, sin importar su masa.

⭐ Fórmulas de Caída Libre (Formulario)
Aquí tienes las herramientas matemáticas. Recuerda que usamos la gravedad como constante.
Valor de la Gravedad (g)
Para estos ejercicios usaremos el valor estándar:
\[ g = 9.8 \, \frac{\text{m}}{\text{s}^2} \]
Las 3 fórmulas maestras son:
1. Velocidad Final:
\[ v_f = v_0 + gt \]
2. Altura (Posición):
\[ h = v_0 t + \frac{1}{2}gt^2 \]
3. Velocidad sin tiempo:
\[ v_f^2 = v_0^2 + 2gh \]
Donde:
- \(v_f\) = Velocidad final (m/s)
- \(v_0\) = Velocidad inicial (m/s) (Suele ser 0)
- \(t\) = Tiempo (s)
- \(h\) = Altura (m)
- \(g\) = Gravedad ($9.8 \text{ m/s}^2$)
✅ Ejercicios Resueltos de Caída Libre
Vamos a resolver los problemas más comunes de exámenes, incluyendo los de la Ciudad de México y balones lanzados.
Problema 1: Balón desde Edificio
Se deja caer un balón desde la azotea de un edificio que tiene una altura de 13 m. ¿En qué tiempo toca el piso?
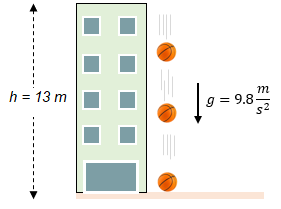
Solución:
Como dice "se deja caer", sabemos que \(v_0 = 0\). Usamos la fórmula de altura y despejamos el tiempo.
\[ h = \frac{gt^2}{2} \Rightarrow t = \sqrt{\frac{2h}{g}} \]
Sustituyendo datos:
\[ t = \sqrt{\frac{2(13 \text{ m})}{9.8 \text{ m/s}^2}} \]
\[ t = \sqrt{\frac{26}{9.8}} = \sqrt{2.65} \]
\[ t = 1.63 \text{ s} \]
Resultado: Tarda 1.63 segundos en caer.
Problema 2: Edificio en Ciudad de México
Un cuerpo se deja caer desde un edificio de la ciudad de México. Calcular:
a) ¿Cuál será la velocidad final a los 10 segundos?
b) ¿Cuál es la altura del edificio?
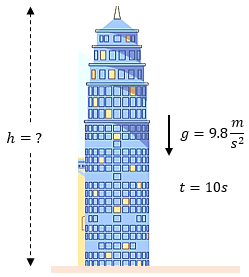
Solución:
Datos: \(v_0 = 0\), \(t = 10 \text{ s}\), \(g = 9.8 \text{ m/s}^2\).
a) Velocidad Final:
\[ v_f = v_0 + gt = 0 + (9.8)(10) \]
\[ v_f = 98 \text{ m/s} \]
b) Altura del Edificio:
\[ h = \frac{gt^2}{2} = \frac{(9.8)(10)^2}{2} \]
\[ h = \frac{9.8(100)}{2} = \frac{980}{2} = 490 \text{ m} \]
Resultado: Velocidad de 98 m/s y altura de 490 metros.
Problema 3: Pelota de Básquetbol
Se deja caer una pelota de básquetbol desde una altura de 90 metros. Calcular:
a) El tiempo que demora en caer.
b) La velocidad con la que llega al suelo.
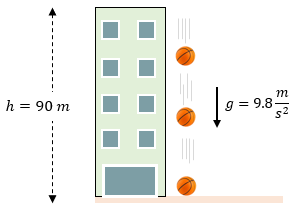
Solución:
a) Tiempo de caída:
\[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(90)}{9.8}} \]
\[ t = \sqrt{\frac{180}{9.8}} = \sqrt{18.36} = 4.28 \text{ s} \]
b) Velocidad de impacto:
\[ v_f = gt = (9.8)(4.28) = 41.9 \text{ m/s} \]
Resultado: Tiempo 4.28 s y velocidad 41.9 m/s.
Problema 4: Balón a 120 metros
Un balón de fútbol se deja caer desde una altura de 120 m. Obtenga:
a) ¿Qué altura habrá recorrido a los 3 s?
b) ¿Qué velocidad tiene a los 3 s?
c) ¿Cuánto le falta recorrer para llegar al piso?
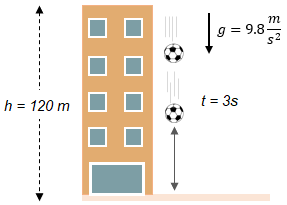
Solución:
a) Distancia recorrida en 3s:
\[ h_3 = \frac{gt^2}{2} = \frac{9.8(3)^2}{2} = \frac{9.8(9)}{2} = 44.1 \text{ m} \]
b) Velocidad a los 3s:
\[ v_f = gt = (9.8)(3) = 29.4 \text{ m/s} \]
c) Distancia faltante:
\[ h_{\text{falta}} = h_{\text{total}} - h_{\text{recorrida}} \]
\[ h_{\text{falta}} = 120 \text{ m} - 44.1 \text{ m} = 75.9 \text{ m} \]
Problema 5: Caso Especial (Tiro Vertical)
Un cuerpo es lanzando verticalmente hacía arriba con una velocidad inicial de 30 m/s. Calcule la altura máxima y el tiempo de vuelo.
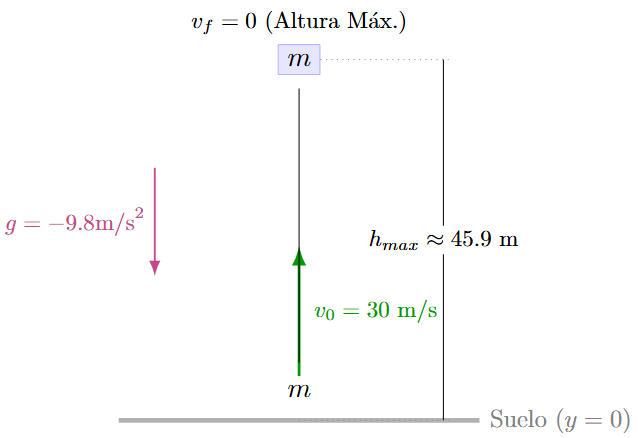
Solución:
Nota: Este es un problema de Tiro Vertical. Si quieres profundizar en este tema (lanzamientos hacia arriba), visita nuestro artículo especializado sobre Tiro Vertical.
Datos: \(v_0 = 30 \text{ m/s}\), \(v_f = 0\) (en la altura máxima), \(g = -9.8 \text{ m/s}^2\).
Tiempo de subida:
\[ t = \frac{v_f - v_0}{g} = \frac{0 - 30}{-9.8} = 3.06 \text{ s} \]
Altura Máxima:
\[ h = v_0 t + \frac{1}{2}gt^2 = (30)(3.06) - 0.5(9.8)(3.06)^2 \]
\[ h = 91.8 - 45.88 = 45.92 \text{ m} \]
🚀 Más Ejercicios de Examen
Problema 6: Cálculo de Altura Máxima
Un objeto se deja caer desde 500 cm. Calcular la altura máxima desde el suelo si tarda 2.5 s en llegar al suelo. (Usa \( g = 9.8 \, \text{m/s}^2 \)).
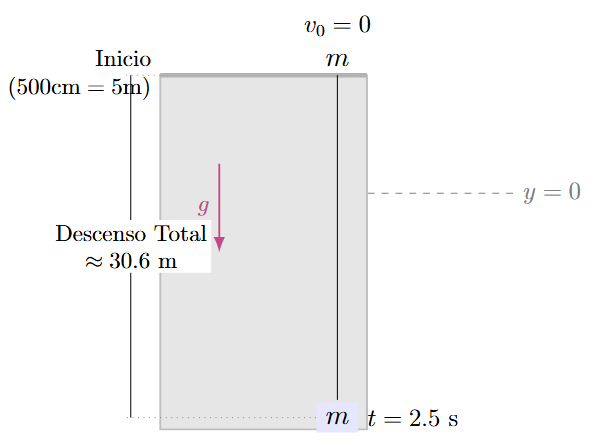
Solución:
Cuidado con las unidades: \(h_0 = 500 \text{ cm} = 5 \text{ m}\).
El problema plantea una caída de 2.5s. La distancia que cae en ese tiempo es:
\[ h_{\text{caída}} = 0.5(9.8)(2.5)^2 = 30.625 \text{ m} \]
Si partió de 5m de altura, esto físicamente implica que había un pozo o desnivel, llegando a una posición final de:
\[ h_f = 5 \text{ m} - 30.625 \text{ m} = -25.625 \text{ m} \]
Resultado: El objeto descendió 30.6 metros en total.
Problema 7: Caída de 2 Kilómetros
Un objeto se deja caer desde una altura de 2 km. Calcular la distancia que ha descendido después de 10 s.
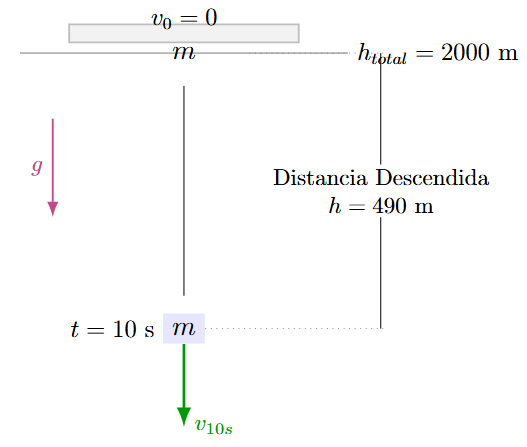
Solución:
Datos: \(h_{total} = 2000 \text{ m}\). Nos piden distancia a los \(t=10\).
\[ h = \frac{1}{2}(9.8)(10)^2 = 4.9(100) = 490 \text{ m} \]
Resultado: Ha descendido 490 metros.
Problema 8: Pinza Mecánica
Una pinza mecánica se deja caer desde una altura de 100 m. Calcular su velocidad final al llegar al suelo.
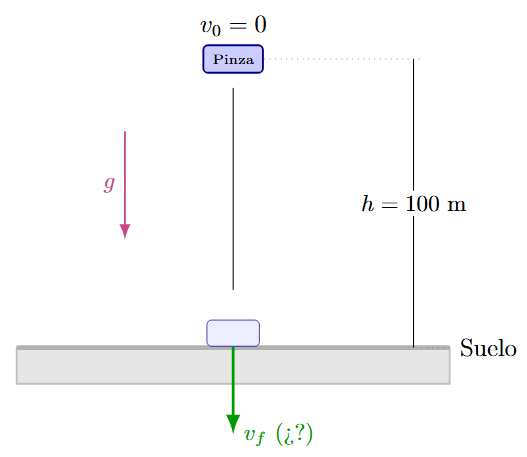
Solución:
Usamos la fórmula que no depende del tiempo: \(v_f = \sqrt{2gh}\).
\[ v_f = \sqrt{2(9.8)(100)} = \sqrt{1960} \]
\[ v_f = 44.27 \text{ m/s} \]
Problema 9: El Anillo
Un anillo se deja caer desde una altura de 45 m. Calcular el tiempo que tarda en llegar al suelo.

Solución:
\[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(45)}{9.8}} = \sqrt{\frac{90}{9.8}} \]
\[ t = \sqrt{9.18} = 3.03 \text{ s} \]
Problema 10: Lanzamiento hacia Abajo
Un reloj se lanza hacia abajo con una velocidad inicial de 15 m/s desde una altura de 80 m. Calcular el tiempo que tarda en llegar al suelo.
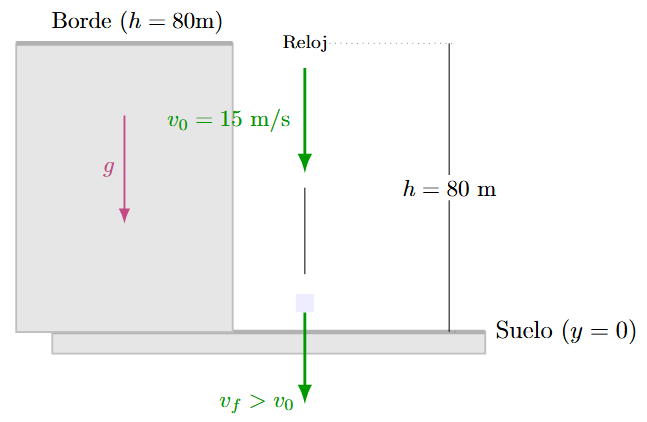
Solución:
Aquí \(v_0 \neq 0\).
\[ h = v_0 t + \frac{1}{2}gt^2 \Rightarrow 80 = 15t + 4.9t^2 \]
Ecuación cuadrática: \(4.9t^2 + 15t - 80 = 0\).
Usando la fórmula general:
\[ t = \frac{-15 \pm \sqrt{15^2 - 4(4.9)(-80)}}{2(4.9)} \]
\[ t = \frac{-15 \pm \sqrt{225 + 1568}}{9.8} = \frac{-15 \pm 42.34}{9.8} \]
Tomamos la raíz positiva:
\[ t = \frac{27.34}{9.8} = 2.79 \text{ s} \]
Resultado: Tarda 2.79 segundos.
Ejercicios para Practicar de Caída Libre
Pon a prueba lo aprendido. Intenta resolverlos antes de ver la solución.
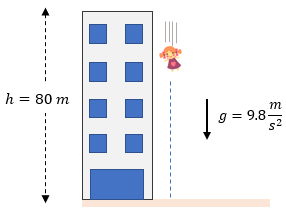
Problema Práctico 1: La Muñeca
Una niña deja caer una muñeca desde una ventana que está a 80 metros de altura.
a) ¿Qué tiempo tardará en caer?
b) ¿Con qué velocidad choca contra el suelo?
▶︎ Haz clic aquí para ver la solución
a) Tiempo: \( t = \sqrt{2(80)/9.8} = 4.04 \text{ s} \)
b) Velocidad: \( v_f = (9.8)(4.04) = 39.59 \text{ m/s} \)
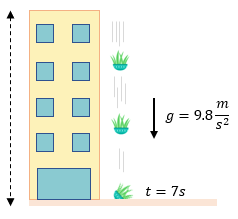
Problema Práctico 2: La Maceta
Una maceta cae desde la azotea y tarda 7 segundos en llegar al suelo.
a) Calcular la altura del edificio.
b) Calcular la velocidad de impacto.
▶︎ Haz clic aquí para ver la solución
a) Altura: \( h = 0.5(9.8)(7)^2 = 240.1 \text{ m} \)
b) Velocidad: \( v_f = (9.8)(7) = 68.6 \text{ m/s} \)
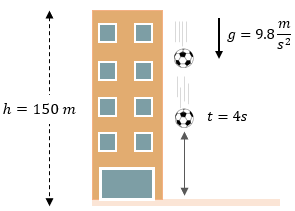
Problema Práctico 3: Descenso en 4 segundos
Desde una altura de 150 metros se deja caer una pelota.
a) ¿Cuánto ha descendido a los 4 segundos?
b) ¿Cuánto le falta recorrer?
▶︎ Haz clic aquí para ver la solución
a) Descendido: \( h = 0.5(9.8)(4)^2 = 78.4 \text{ m} \)
b) Falta: \( 150 - 78.4 = 71.6 \text{ m} \)
Descargar PDF de Caída Libre (20 Ejercicios)
¿Necesitas más material? Hemos recopilado 20 problemas resueltos que incluyen gráficas de posición vs tiempo y problemas de mayor dificultad. No olvides que también puedes aprender más de Cinemática y temas de gran relevancia como el Tiro Parabólico.
🔒 Incluye Tiro Vertical y Gráficas • 100% Gratis
Examen de Caída Libre
Es momento de aclarar tus dudas con este pequeño examen.
Cargando examen...
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Muy buen trabajo y muy útil, felicidades y gracias!
-
Saludos le agradezco q me ayude en este ejercicio pasó por pasó
Con que velocidad toca un cuerpo él suelo que se deja caer y tarda 15 segundos en caer-
V = g * t
V = 9,8 * 15 = 147 m/s
-
-
un cuerpo de 50kilogramo es dejando caer libremente y tarda dos segúndo en tocar el suelo calcular
-
-
Porque en el C. Porque restaste 91,8 - 45,8? No deberia ser suma?
-
Gracias.
Y me equivoqué, me refiero al primer inciso del segundo problema donde se debe calcular la velocidad que tendrá a los 2 segundos. La fórmula que usas es: V= V0 + gt. Al multiplicar la aceleración de la gravedad por el tiempo, da como resultado 19.6, y eso habría que sumarlo a la velocidad inicial (30), pero tú se lo restaste y dio como resultado 10.4. Me preguntaba por qué se lo habías restado, si la fórmula (V=V0 + gt) dice que hay que sumarlo. Pero ayer me di cuenta que esto es porque el valor de aceleración de gravedad, es negativo en este caso, ¿es por eso que se lo restaste a 30, en vez de sumarlo?
Espero que me hayas entendido. Un saludo. Me suscribo.
-
Un carro va por una carretera con una rapidez constante de 20m/seg que mantiene durante 2 min. A continuación acelera a razón de 3 m/seg2 durante 20 seg. Calcular la distancia total recorrida
-
Hola, no entiendo pq en el tercer problema la fórmula dice
D= v⁰ t + 1/2gt²
Y cuando reemplazas pones - y no +
:'V
-
-
un sumatorio pasa al otro ldo del igual restando
30 = Vi + 9,8 * 2 ------- 30 - 19,6 = Vi --------- Vi = 10,4 m/s
-
-
Hola, gracias y felicidades por tu trabajo. Estoy repasando este tema, pero tengo dudas.
Necesito calcular el tiempo que tarda en caer una manzana que tiene una velocidad de 100 m/s, pero no menciona altura ni nada. ¿Basta con que divida la velocidad sobre la aceleración de gravedad? Si lo hago así, da como resultado 10.2 s, ¿es correcto?
Otra cosa, en el segundo ejercicio, donde se pide calcular la velocidad que alcanzará el cuerpo a los 2 segundos, veo que restaste 19.6 a la velocidad inicial (40), ¿por qué? Conozco una fórmula para determinar la velocidad, que es: V= at y da como resultado 19.6, pero no entiendo por qué se lo restas a 40.
-
me puedes ayudar con este problema: Una niña deja caer una muñeca desde una ventana que está a 80 metros de la altura sobre el suelo. Calcular, a) ¿Qué tiempo tardará en caer?, b) ¿Con qué magnitud de velocidad choca contra el suelo?
-
Una pelota va rodando por el suelo a una velocidad de 8 m/seg, y llega al borde de la escalera. Si cada escalón tiene una altura de 0,18 cm y el ancho del paso es de 0,25 cm, ¿en qué escalón caerá la pelota? Esto es un ejercicio de caída libre?
-
Vf = Vi + g * t
40 = Vi + 9,81 * 2
40 - 19,6 = Vi
Vi = 20,4 m/s -
Vf = Vi + g * t --------- 40 m/s = Vi + 9,8 * 2----------- 40 - 19,6 = Vi ------- Vi = 20,4 m/s
-
Vf = Vi + g * t
40 m/s = Vi + 9,8 * 2
40 - 19,6 = Vi
Vi = 20,4 m/s
-
-
Buenas tardes.. soy estudiante y tengo una formula mas rápida para encontrar la altura máxima o distancia máxima que nos pides en tu problema#2-.. espero sea mas útil en cuestión del tiempo en realizar la otra formula mas larga:
h= gt ^2/ 2
Aun así Gracias por tus explicaciones .
att:
Alex Longoria
Técnico en urgencias medicas y Técnico en emergencias medias.-
Gracias me gusta como explica pongan más ejercicios.asi bien detallados paso x paso
-
Buenas noches. Podrían ayudarme con estos dos ejercicios de caida libre por fa.
1) un movil en caida libre pasa por el puntoA con un velocidad de 10 m/s y por el punto B con una velocidad de 30 m/s. Hallar cuanto tarda en pasar del punto A al punto B
2) un cuerpo en caida libre pasa por el punto A con una velocidad de 10m/s y por el punto B una velocidad de 20 m/s . Hallar la distancia entre los puntos A y B.-
Hola me puedes ayudar con un ejercicio de caida libre por favor dice asi. Desde lo alto de un edificio se deja caer un cuerpo que llega al suelo con una rapidez de 20 m/s. Calcular a) altura del edificio.b) distancia recorrida a los 2 seg. C) la rapidez que tiene a los 2seg.D) la rapidez cuando haya descendido 45m. Te lo agradezco
-
-
Gracias 🙂
-
262 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar