División de un Segmento En Una Razón Dada - Ejemplos
Bienvenidos nuevamente a un tema fundamental de la Geometría Analítica. Si alguna vez te has preguntado cómo encontrar las coordenadas exactas de un punto que divide a una carretera, un cable o una recta en dos partes proporcionales, estás en el lugar correcto.
Hoy no solo aprenderemos la fórmula; entenderemos la lógica detrás de ella. Vamos a desglosar paso a paso la división de un segmento en una razón dada, un concepto que une el álgebra con la geometría y que es la base para entender temas más avanzados como los centros de gravedad en física.
Lo que aprenderás hoy
- ¿Qué significa realmente "razón" en geometría?
- Cómo deducir la fórmula sin memorizarla a ciegas.
- El caso especial (y muy buscado): el Punto Medio.
- 10 Ejercicios: 5 resueltos paso a paso y 5 para practicar (con solución).
¿Qué es la División de un Segmento en una Razón Dada?
Imagina que tienes un segmento de recta con dos extremos, \(P_1(x_1, y_1)\) y \(P_2(x_2, y_2)\). Si colocamos un tercer punto \(P(x, y)\) sobre esa línea, este punto dividirá al segmento original en dos partes.
La comparación (división) entre la longitud de la primera parte y la longitud de la segunda parte se llama razón y se denota con la letra \(r\).
Definición Matemática
La razón \(r\) es el cociente entre la distancia dirigida desde el punto inicial \(P_1\) al punto de división \(P\), y la distancia dirigida desde \(P\) al punto final \(P_2\):
\[ r = \frac{P_1P}{PP_2} \]
Hasta aquí suena sencillo, pero hay un detalle que suele confundir a los estudiantes y que vamos a aclarar ahora mismo:
⚠️ El Signo de la Razón Importa
El valor de \(r\) nos dice dónde está ubicado el punto \(P\):
- Si \(r > 0\) (Positiva): El punto \(P\) está dentro del segmento \(P_1P_2\) (División Interna).
- Si \(r < 0\) (Negativa): El punto \(P\) está fuera del segmento, es decir, en la prolongación de la recta (División Externa).
Obtención de la Fórmula: Deducción Paso a Paso
Para no ser "robots" que solo aplican fórmulas, vamos a ver de dónde sale. Usaremos el Teorema de Tales (semejanza de triángulos) para demostrarlo. Observa la siguiente gráfica:

Analicemos la proyección en el plano cartesiano:
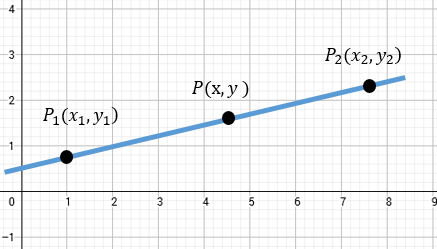
Si proyectamos las coordenadas sobre los ejes \(x\) e \(y\), se forman triángulos semejantes. Por la propiedad de proporcionalidad, la razón entre las distancias inclinadas es igual a la razón entre sus proyecciones horizontales y verticales.
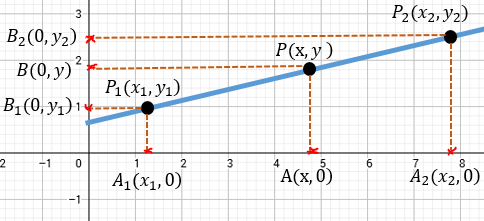
Centrémonos en el eje \(x\) (abscisas). La relación es:
\[ r = \frac{P_1P}{PP_2} = \frac{A_1A}{AA_2} \]
Recordando el concepto de distancia dirigida (posición final menos posición inicial):
- Distancia \(A_1A = x - x_1\)
- Distancia \(AA_2 = x_2 - x\)
Sustituyendo esto en la ecuación de la razón:
\[ r = \frac{x - x_1}{x_2 - x} \]
Nuestro objetivo es encontrar \(x\). Así que, si recuerdas tus clases de álgebra básica (o si necesitas repasar cómo despejar fórmulas), procedemos así:
1. Pasamos el denominador multiplicando al lado izquierdo:
\[ r(x_2 - x) = x - x_1 \]
2. Desarrollamos la multiplicación:
\[ rx_2 - rx = x - x_1 \]
3. Agrupamos los términos que tienen \(x\) en un lado y los que no, en el otro:
\[ rx_2 + x_1 = x + rx \]
4. Factorizamos \(x\) (factor común):
\[ x_1 + rx_2 = x(1 + r) \]
5. Finalmente, despejamos \(x\):
\[ x = \frac{x_1 + rx_2}{1 + r} \]
¡Eureka! Hemos encontrado la fórmula para la coordenada \(x\). Para la coordenada \(y\), el proceso es idéntico geométricamente, resultando en:
\[ y = \frac{y_1 + ry_2}{1 + r} \]
Existe una única condición matemática importante para que esto no "explote":
\[ r \neq -1 \]
(Porque si \(r = -1\), tendríamos una división por cero).
Resumen de Fórmulas
Fórmulas de División de un Segmento
Para calcular las coordenadas \(P(x, y)\) que dividen al segmento \(P_1P_2\) en una razón \(r\):
\[ x = \frac{x_1 + rx_2}{1+r} \]
\[ y = \frac{y_1 + ry_2}{1+r} \]
El Caso Especial: Fórmula del Punto Medio
Muchos ejercicios te pedirán simplemente el "punto medio". Esto es un caso particular donde el punto \(P\) está exactamente a la mitad. Por lo tanto, la distancia \(P_1P\) es igual a \(PP_2\), lo que significa que:
\[ r = \frac{P_1P}{PP_2} = 1 \]
Si sustituimos \(r=1\) en nuestras fórmulas generales, obtenemos un promedio simple:
\[ x_{pm} = \frac{x_1 + x_2}{2}, \quad y_{pm} = \frac{y_1 + y_2}{2} \]
5 Ejemplos Resueltos de División de un Segmento
La mejor forma de aprender matemáticas es "arrastrando el lápiz". Vamos a resolver 5 casos diferentes para cubrir cualquier tipo de pregunta que te puedan hacer en un examen.
Ejemplo 1: Razón Positiva (Fracción)
Hallar las coordenadas del punto \(P(x,y)\) que divide al segmento determinado por \(A(5, 3)\) y \(B(-2, 8)\) en la razón \(r = 3/4\).
Solución:
Identificamos nuestros datos:
- \(P_1 (A): x_1 = 5, y_1 = 3\)
- \(P_2 (B): x_2 = -2, y_2 = 8\)
- Razón \(r = 3/4 = 0.75\)
Paso 1: Calcular \(x\)
\[ x = \frac{5 + (\frac{3}{4})(-2)}{1 + \frac{3}{4}} \]
\[ x = \frac{5 - \frac{6}{4}}{\frac{7}{4}} = \frac{\frac{20}{4} - \frac{6}{4}}{\frac{7}{4}} = \frac{\frac{14}{4}}{\frac{7}{4}} \]
Aplicando la ley del sándwich (o extremos por extremos):
\[ x = \frac{14 \cdot 4}{7 \cdot 4} = \frac{14}{7} = 2 \]
Paso 2: Calcular \(y\)
\[ y = \frac{3 + (\frac{3}{4})(8)}{1 + \frac{3}{4}} \]
\[ y = \frac{3 + \frac{24}{4}}{\frac{7}{4}} = \frac{3 + 6}{1.75} = \frac{9}{1.75} \approx 5.14 \]
Resultado: El punto es \(P(2, 5.14)\).
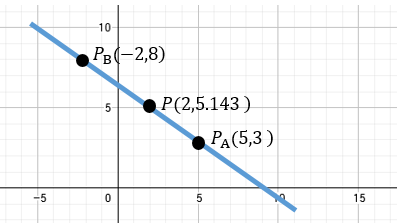
Ejemplo 2: Aplicación en Geometría (Centro de una Circunferencia)
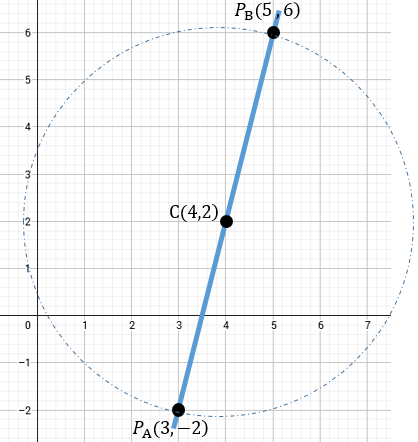
Los extremos del diámetro de una circunferencia son \(A(3, -2)\) y \(B(5, 6)\). Encuentra las coordenadas del centro.
Solución:
Este es un problema de Punto Medio disfrazado. El centro siempre está a la mitad del diámetro. Por lo tanto, \(r=1\).
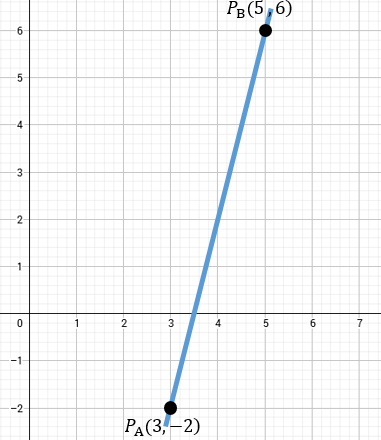
Usamos la fórmula simplificada:
\[ x = \frac{3 + 5}{2} = \frac{8}{2} = 4 \]
\[ y = \frac{-2 + 6}{2} = \frac{4}{2} = 2 \]
Resultado: El centro es \(C(4, 2)\).
Ejemplo 3: Razón Racional
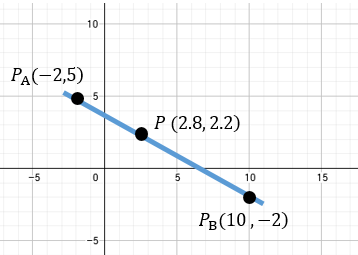
Hallar las coordenadas del punto \(P\) que divide al segmento \(A(-2, 5)\) y \(B(10, -2)\) en la razón \(r = 2/3\).
Solución:
Datos: \(x_1 = -2, y_1 = 5\) y \(x_2 = 10, y_2 = -2\).
Para la abscisa (x):
\[ x = \frac{-2 + (\frac{2}{3})(10)}{1 + \frac{2}{3}} = \frac{-2 + \frac{20}{3}}{\frac{5}{3}} \]
\[ x = \frac{\frac{-6+20}{3}}{\frac{5}{3}} = \frac{14}{5} = 2.8 \]
Para la ordenada (y):
\[ y = \frac{5 + (\frac{2}{3})(-2)}{1 + \frac{2}{3}} = \frac{5 - \frac{4}{3}}{\frac{5}{3}} \]
\[ y = \frac{\frac{15-4}{3}}{\frac{5}{3}} = \frac{11}{5} = 2.2 \]
Resultado: \(P(2.8, 2.2)\).
Ejemplo 4: División Externa (Razón Negativa)
Determina las coordenadas del punto \(P\) que divide al segmento \(A(-4, 2)\) y \(B(2, -1)\) en una razón \(r = -3\).
Solución:
¡Ojo aquí! Como \(r = -3\), esperamos que el punto \(P\) esté fuera del segmento. Aplicamos la fórmula con mucho cuidado con los signos.
Cálculo de x:
\[ x = \frac{x_1 + r x_2}{1 + r} = \frac{-4 + (-3)(2)}{1 + (-3)} \]
\[ x = \frac{-4 - 6}{-2} = \frac{-10}{-2} = 5 \]
Cálculo de y:
\[ y = \frac{y_1 + r y_2}{1 + r} = \frac{2 + (-3)(-1)}{1 + (-3)} \]
\[ y = \frac{2 + 3}{-2} = \frac{5}{-2} = -2.5 \]
Resultado: El punto es \(P(5, -2.5)\). Efectivamente, está fuera del segmento original.
Ejemplo 5: Encontrar la Razón dados los Puntos
¿En qué razón divide el punto \(P(2, 0)\) al segmento formado por \(A(0, 4)\) y \(B(5, -6)\)?
Solución:
Aquí la incógnita es \(r\). Podemos usar cualquiera de las dos fórmulas (\(x\) o \(y\)) para despejarla. Usaremos la de \(x\).
\[ x = \frac{x_1 + r x_2}{1 + r} \]
Sustituimos los valores conocidos (\(x=2, x_1=0, x_2=5\)):
\[ 2 = \frac{0 + r(5)}{1 + r} \]
Despejamos \(r\):
\[ 2(1 + r) = 5r \]
\[ 2 + 2r = 5r \]
\[ 2 = 5r - 2r \]
\[ 2 = 3r \Rightarrow r = \frac{2}{3} \]
Resultado: La razón es \(r = 2/3\). (Puedes comprobarlo con la fórmula de \(y\), te dará lo mismo).
💡 ¡Sabías Qué!
Si la razón calculada hubiera sido 1, significaría que el punto \(P\) es el punto medio. Si hubiera sido negativa, \(P\) estaría fuera del segmento.
Ejercicios Propuestos para Practicar
Para dominar este tema, necesitas practicar. Intenta resolver estos 5 problemas adicionales. Si completas estos, habrás resuelto un total de 10 ejemplos de división de un segmento.
Problema Propuesto 1
Encuentra el punto medio del segmento formado por los puntos \(A(6, 4)\) y \(B(-2, -2)\).
Haz clic aquí para ver la solución
Usamos \(r=1\) (Punto medio).
\(x = \frac{6 + (-2)}{2} = \frac{4}{2} = 2\)
\(y = \frac{4 + (-2)}{2} = \frac{2}{2} = 1\)
Respuesta: \(P(2, 1)\)
Problema Propuesto 2
Dados \(P_1(1, -3)\) y \(P_2(4, 3)\), halla el punto \(P\) que divide al segmento en una razón \(r = 2\).
Haz clic aquí para ver la solución
\(x = \frac{1 + 2(4)}{1 + 2} = \frac{9}{3} = 3\)
\(y = \frac{-3 + 2(3)}{1 + 2} = \frac{3}{3} = 1\)
Respuesta: \(P(3, 1)\)
Problema Propuesto 3 (Fracciones)
Si \(A(-5, 2)\) y \(B(1, 4)\), encuentra \(P(x,y)\) dado que \(r = 1/2\).
Haz clic aquí para ver la solución
\(x = \frac{-5 + (0.5)(1)}{1.5} = \frac{-4.5}{1.5} = -3\)
\(y = \frac{2 + (0.5)(4)}{1.5} = \frac{4}{1.5} = \frac{8}{3} \approx 2.66\)
Respuesta: \(P(-3, 8/3)\)
Problema Propuesto 4 (División Externa)
Encuentra el punto que divide al segmento \(M(2, 5)\) y \(N(4, 2)\) en una razón \(r = -2\).
Haz clic aquí para ver la solución
\(x = \frac{2 + (-2)(4)}{1 - 2} = \frac{-6}{-1} = 6\)
\(y = \frac{5 + (-2)(2)}{1 - 2} = \frac{1}{-1} = -1\)
Respuesta: \(P(6, -1)\)
Problema Propuesto 5 (Hallar la razón)
¿En qué razón divide el eje \(x\) al segmento formado por \(A(2, 4)\) y \(B(5, -2)\)?
Pista: Si el punto está en el eje x, su coordenada y es 0.
Haz clic aquí para ver la solución
Sabemos que en el eje \(x\), la coordenada \(y = 0\). Usamos la fórmula de \(y\):
\(0 = \frac{4 + r(-2)}{1+r}\)
Para que una fracción sea cero, el numerador debe ser cero:
\(4 - 2r = 0 \Rightarrow 4 = 2r \Rightarrow r = 2\)
Respuesta: \(r = 2\)
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado la División de un Segmento en una Razón Dada y has resuelto 10 ejercicios clave. Ahora sabes calcular coordenadas internas, externas y encontrar razones.
Este tema es una pieza fundamental del rompecabezas. Te recomendamos visitar nuestro artículo pilar sobre Geometría Analítica para ver cómo conectar esto con la línea recta, las cónicas y mucho más.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
muy interesante sus ejercicios, pero seria mucho mas, si pueden poner mas ejercicios para resolver
-
hubiera sido mejor si dejaba unos ejercicios mas para paracticar
19 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar