Ecuación de la Elipse con Centro en el Origen
La forma de la elipse juega un papel estelar en el universo. No es casualidad que las Leyes de Kepler demostraran que los planetas no giran en círculos perfectos, sino en órbitas elípticas. Pero, ¿qué es exactamente una elipse y cómo se "domestica" matemáticamente?
En este artículo, diseñado para ser la guía definitiva de Geometría Analítica, aprenderás desde cero a identificar, calcular y graficar la ecuación de la elipse con centro en el origen.
¿Qué es una Elipse? Definición Geométrica
Imagina que clavas dos tachuelas en una mesa y atas un hilo holgado entre ellas. Si estiras el hilo con un lápiz y lo mueves alrededor, dibujarás una elipse. Esas tachuelas son los Focos.
Definición Formal
La Elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de sus distancias a dos puntos fijos (llamados Focos) es siempre constante e igual a la longitud del eje mayor (2a).
Elementos y Fórmulas de la Elipse (Formulario)
Para dominar la elipse, necesitas entender sus tres protagonistas principales. Memoriza esto, porque es la clave de todo:
- a: Distancia del centro al Vértice (es la mitad del eje mayor). ¡Siempre es el valor más grande!
- b: Distancia del centro al extremo del eje menor.
- c: Distancia del centro al Foco.
Existe una "regla de oro" que conecta estas tres variables (muy parecida a Pitágoras):
\[ a^2 = b^2 + c^2 \]
💡 El Truco para Identificarla
¿Cómo saber si una ecuación es Horizontal o Vertical sin graficar?
Simplemente mira los denominadores. La letra que tenga el número más grande abajo, define la orientación.
- Si el número mayor está bajo la X → Es Horizontal (acostada).
- Si el número mayor está bajo la Y → Es Vertical (parada).
1. Elipse Horizontal
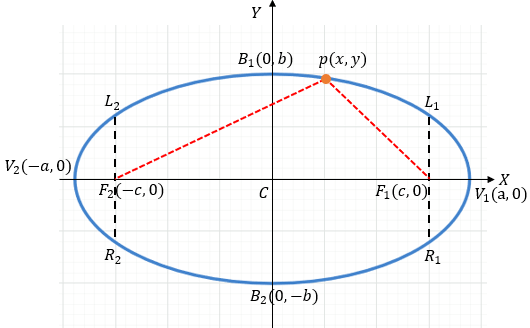
El eje mayor coincide con el eje X. Observa que el valor \( a^2 \) está debajo de la \( x \).
Ecuación Canónica
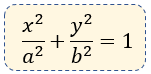
Elementos:
- Vértices: \( V(\pm a, 0) \)
- Focos: \( F(\pm c, 0) \)
- Extremos eje menor: \( B(0, \pm b) \)
2. Elipse Vertical
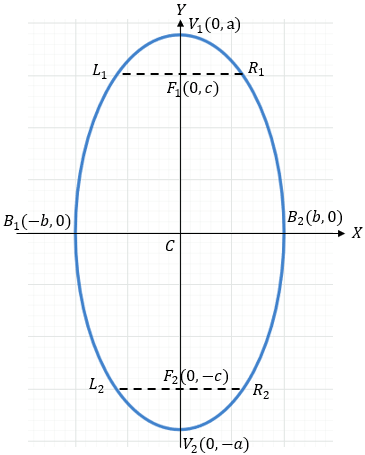
El eje mayor coincide con el eje Y. Aquí el valor mayor \( a^2 \) está debajo de la \( y \).
Ecuación Canónica
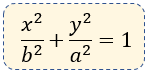
Elementos:
- Vértices: \( V(0, \pm a) \)
- Focos: \( F(0, \pm c) \)
- Extremos eje menor: \( B(\pm b, 0) \)
Fórmulas Comunes (Para ambos casos)
- Lado Recto (Ancho focal):
\[ LR = \frac{2b^2}{a} \] - Excentricidad (Qué tan achatada es):
\[ e = \frac{c}{a} \quad (Siempre \ e < 1) \]
Ejercicios Resueltos Paso a Paso
La teoría está muy bien, pero la práctica hace al maestro. Vamos a resolver problemas tipo examen, desde lo básico hasta análisis inverso.
Ejemplo 1: De Ecuación General a Elementos (Vertical)
Determina los elementos y grafica la elipse dada por la ecuación: \( 9x^2 + 4y^2 - 36 = 0 \)
Solución:
Nuestro objetivo es llegar a la forma canónica \( \frac{x^2}{?} + \frac{y^2}{?} = 1 \).
Paso 1: Ordenar la ecuación.
Movemos el término independiente al lado derecho:
\[ 9x^2 + 4y^2 = 36 \]
Paso 2: Dividir para igualar a 1.
Dividimos toda la ecuación entre 36:
\[ \frac{9x^2}{36} + \frac{4y^2}{36} = \frac{36}{36} \]
Simplificamos las fracciones (\( 9/36 = 1/4 \) y \( 4/36 = 1/9 \)):
\[ \frac{x^2}{4} + \frac{y^2}{9} = 1 \]
Paso 3: Análisis de orientación.
Observa los denominadores: 4 y 9. El número mayor es 9 y está debajo de la Y.
¡Es una Elipse Vertical!
Por tanto:
\[ a^2 = 9 \rightarrow a = 3 \]
\[ b^2 = 4 \rightarrow b = 2 \]
Paso 4: Calcular c (distancia focal).
Usamos \( c = \sqrt{a^2 - b^2} \):
\[ c = \sqrt{9 - 4} = \sqrt{5} \approx 2.23 \]
Paso 5: Elementos Finales.
- Vértices \( V(0, \pm a) \): \( V_1(0, 3) \) y \( V_2(0, -3) \)
- Focos \( F(0, \pm c) \): \( F_1(0, \sqrt{5}) \) y \( F_2(0, -\sqrt{5}) \)
- Extremos menor \( B(\pm b, 0) \): \( B_1(2, 0) \) y \( B_2(-2, 0) \)
- Lado Recto: \( LR = \frac{2(2)^2}{3} = \frac{8}{3} \approx 2.66 \)
- Excentricidad: \( e = \frac{\sqrt{5}}{3} \approx 0.745 \)
Gráfica:
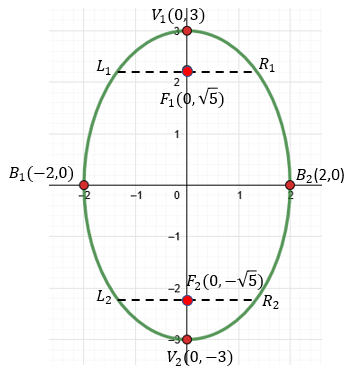
Ejemplo 2: De Ecuación General a Elementos (Horizontal)
Determina los elementos y grafica la elipse: \( 16x^2 + 25y^2 - 400 = 0 \)
Solución:
Paso 1: Despejar e Igualar a 1.
\[ 16x^2 + 25y^2 = 400 \]
Dividimos todo entre 400:
\[ \frac{16x^2}{400} + \frac{25y^2}{400} = 1 \]
Simplificando:
\[ \frac{x^2}{25} + \frac{y^2}{16} = 1 \]
Paso 2: Análisis.
El denominador mayor es 25 y está bajo la X. Es una Elipse Horizontal.
- \( a^2 = 25 \rightarrow a = 5 \)
- \( b^2 = 16 \rightarrow b = 4 \)
Paso 3: Calcular c.
\[ c = \sqrt{25 - 16} = \sqrt{9} = 3 \]
Paso 4: Elementos.
- Vértices \( V(\pm 5, 0) \): \( V(5,0), V(-5,0) \)
- Focos \( F(\pm 3, 0) \): \( F(3,0), F(-3,0) \)
- Lado Recto: \( LR = \frac{2(4)^2}{5} = \frac{32}{5} = 6.4 \)
- Excentricidad: \( e = 3/5 = 0.6 \)
Gráfica:
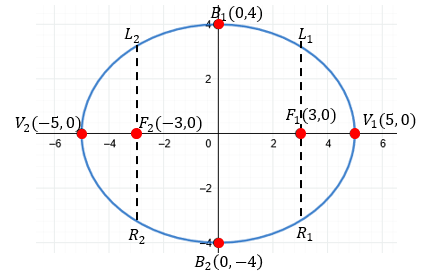
Subiendo la Dificultad: Encontrando la Ecuación
A veces el problema es al revés: te dan los datos y tú debes hallar la fórmula.
Ejemplo 3: Dados Vértice y Foco
Halla la ecuación de la elipse cuyos vértices son los puntos \( V(\pm 5, 0) \) y sus focos son \( F(\pm 3, 0) \).
Solución:
Paso 1: Identificar Orientación.
Como los Vértices y Focos cambian en la coordenada X (y la Y se mantiene en 0), la elipse está sobre el eje X. Es Horizontal.
Paso 2: Obtener a y c.
Del vértice \( (\pm 5, 0) \) deducimos que \( a = 5 \).
Del foco \( (\pm 3, 0) \) deducimos que \( c = 3 \).
Paso 3: Calcular b.
Usamos la relación fundamental \( a^2 = b^2 + c^2 \), despejando \( b \):
\[ b = \sqrt{a^2 - c^2} \]
\[ b = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} \]
\[ b = 4 \]
Paso 4: Sustituir en la fórmula.
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Rightarrow \frac{x^2}{25} + \frac{y^2}{16} = 1 \]
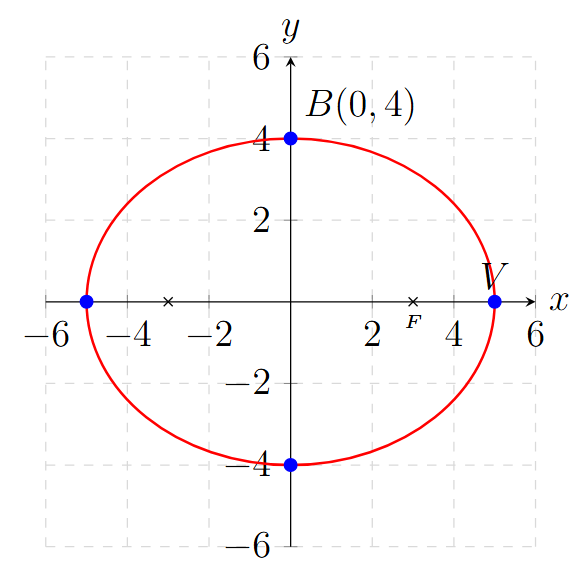
Ejemplo 4: Dada la Longitud del Eje Mayor
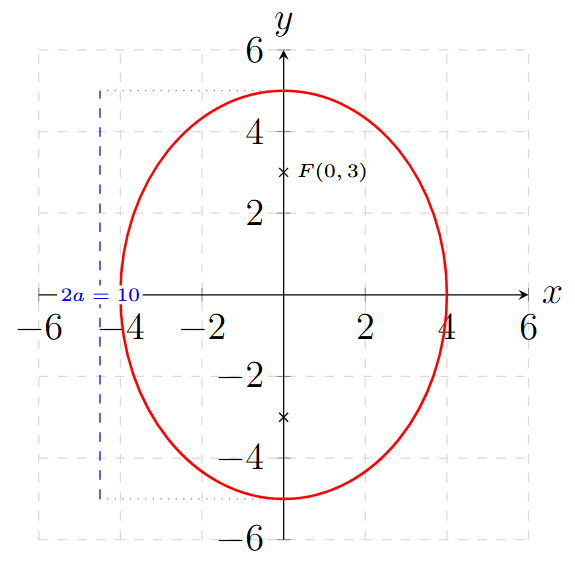
Determina la ecuación de la elipse con centro en el origen, que tiene un foco en \( F(0, 3) \) y la longitud de su eje mayor es de 10 unidades.
Solución:
Análisis: El foco está en \( (0, 3) \), es decir, sobre el eje Y. Es Vertical.
- Dato del foco: \( c = 3 \).
- Dato del eje mayor: Sabemos que la longitud total es \( 2a \).
\[ 2a = 10 \Rightarrow a = \frac{10}{2} = 5 \]
Calcular b:
\[ b = \sqrt{a^2 - c^2} = \sqrt{5^2 - 3^2} = \sqrt{16} = 4 \]
Ecuación (Vertical):
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \Rightarrow \frac{x^2}{16} + \frac{y^2}{25} = 1 \]
Ejemplo 5: Usando la Excentricidad
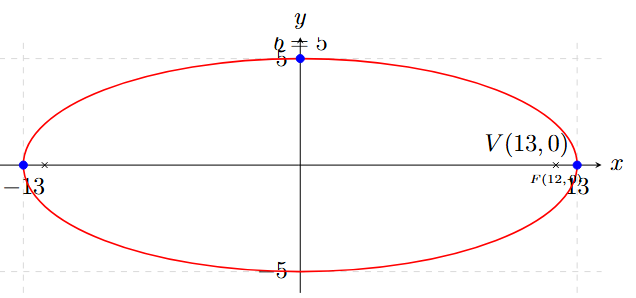
Una elipse horizontal con centro en el origen tiene un vértice en \( (13, 0) \) y una excentricidad de \( e = \frac{12}{13} \). Hallar su ecuación.
Solución:
Este problema requiere usar las definiciones.
1. Como es horizontal y el vértice es \( (13,0) \), sabemos que \( a = 13 \).
2. La fórmula de la excentricidad es \( e = \frac{c}{a} \).
Sustituimos lo que tenemos:
\[ \frac{12}{13} = \frac{c}{13} \]
Por simple inspección (o despeje), vemos que \( c = 12 \).
3. Calculamos \( b \):
\[ b = \sqrt{13^2 - 12^2} = \sqrt{169 - 144} = \sqrt{25} = 5 \]
4. Ecuación:
\[ \frac{x^2}{169} + \frac{y^2}{25} = 1 \]
🚀 ¡Excelente! Siguiente Paso
¡Felicidades! Ahora dominas la elipse con centro en el origen. Sabes calcular sus elementos y deducir su ecuación a partir de datos sueltos.
El siguiente nivel es cuando la elipse se mueve del centro. ¿Te atreves? Continúa con nuestro artículo sobre: Elipse con Vértice Fuera del Origen.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Felicidades el articulo muy bien explicado. Gracias es de bastante utilidad.
-
buena información, me ayudo!
-
esta información me ayudará más adelante, gracias !
-
Gracias, que bien explicado esta el proceso, a ver si hayo la elipse con centro en (h,k)
-
Bien, agradecido por la explicación, fue suficiente
19 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar