Ecuación de la Hipérbola con Centro fuera del Origen
El estudio de la Hipérbola suele ser el "jefe final" en los cursos de Geometría Analítica. Si ya dominas la hipérbola con centro en el origen, dar este paso será muy sencillo: la lógica es la misma, solo que ahora nuestro centro se desplaza a unas coordenadas \((h, k)\).
En este artículo definitivo, no solo veremos las fórmulas "crudas", sino que aprenderás a deducir, graficar y transformar ecuaciones generales a su forma canónica con ejercicios paso a paso. ¡Vamos a ello! 🚀
¿Qué es una Hipérbola con Centro (h,k)?
Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante e igual a \(2a\). Cuando el centro no está en \((0,0)\), decimos que está desplazado a un punto \(C(h,k)\), lo que altera los términos \(x\) e \(y\) en la ecuación estándar.
⚡ Fórmulas y Ecuación Canónica de la Hipérbola (h,k)
Para dominar este tema, primero debemos identificar hacia dónde "se abre" la hipérbola. A diferencia de la elipse (donde mirábamos cuál denominador era mayor), aquí el signo manda. El término positivo indica la dirección de apertura.
1. Hipérbola Horizontal
Si el término con \(x\) es positivo, la hipérbola abraza al eje horizontal (paralelo al eje X). Su eje focal es horizontal.
\[ \frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1 \]
Elementos Clave:
- Centro: \( C(h,k) \)
- Vértices: \( V(h \pm a, k) \)
- Focos: \( F(h \pm c, k) \)
- Extremos del eje conjugado: \( B(h, k \pm b) \)
- Asíntotas: \( y - k = \pm \frac{b}{a}(x - h) \)
2. Hipérbola Vertical
Si el término con \(y\) es positivo, la hipérbola se abre hacia arriba y hacia abajo (paralelo al eje Y). Su eje focal es vertical.
\[ \frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1 \]
Elementos Clave:
- Centro: \( C(h,k) \)
- Vértices: \( V(h, k \pm a) \)
- Focos: \( F(h, k \pm c) \)
- Extremos del eje conjugado: \( B(h \pm b, k) \)
- Asíntotas: \( y - k = \pm \frac{a}{b}(x - h) \)
⚠️ ¡Cuidado con la relación de constantes!
A diferencia de la elipse, en la hipérbola el valor de \(c\) (distancia del centro al foco) es el más grande. La relación pitagórica es:
\[ c^2 = a^2 + b^2 \]
Recuérdalo siempre: aquí se suman los cuadrados.
🧮 Ecuación General de la Hipérbola
A menudo, los ejercicios no nos dan la ecuación "bonita" (canónica), sino la ecuación general desarrollada e igualada a cero:
\[ Ax^2 + Cy^2 + Dx + Ey + F = 0 \]
¿Cómo identificarla? Muy fácil: Los coeficientes \(A\) y \(C\) (los números que acompañan a \(x^2\) y \(y^2\)) deben tener signos contrarios.
📝 Ejercicios Resueltos de Hipérbola fuera del Origen
La mejor forma de aprender es practicando. Vamos a resolver 5 ejercicios que cubren desde lo básico hasta problemas de examen.
Ejemplo 1: De Ecuación General a Canónica (Horizontal)
Determine los elementos y grafique la hipérbola cuya ecuación general es:
\[ 4x^2 - 9y^2 - 16x - 18y - 29 = 0 \]
Solución:
Paso 1: Agrupar términos.
Separamos las \(x\) y las \(y\) en paréntesis, y pasamos la constante al lado derecho:
\[ (4x^2 - 16x) - (9y^2 + 18y) = 29 \]
Paso 2: Factorizar coeficientes principales.
Sacamos el 4 de las \(x\) y el -9 de las \(y\). ¡Ojo con el cambio de signo en la \(y\) al factorizar el negativo!
\[ 4(x^2 - 4x) - 9(y^2 + 2y) = 29 \]
Paso 3: Completar el Trinomio Cuadrado Perfecto.
Dividimos el término lineal entre 2 y lo elevamos al cuadrado. Recuerda sumar lo mismo al otro lado (multiplicado por el factor externo).
\[ 4(x^2 - 4x + 4) - 9(y^2 + 2y + 1) = 29 + 4(4) - 9(1) \]
\[ 4(x-2)^2 - 9(y+1)^2 = 29 + 16 - 9 \]
\[ 4(x-2)^2 - 9(y+1)^2 = 36 \]
Paso 4: Igualar a 1.
Dividimos todo entre 36:
\[ \frac{4(x-2)^2}{36} - \frac{9(y+1)^2}{36} = 1 \Rightarrow \frac{(x-2)^2}{9} - \frac{(y+1)^2}{4} = 1 \]
Análisis de Elementos:
Como la \(x\) es positiva, es Horizontal.
• \(a^2 = 9 \Rightarrow a = 3\)
• \(b^2 = 4 \Rightarrow b = 2\)
• Centro \(C(h,k) = (2, -1)\)
• Foco: \(c = \sqrt{9+4} = \sqrt{13} \approx 3.6\)
Coordenadas:
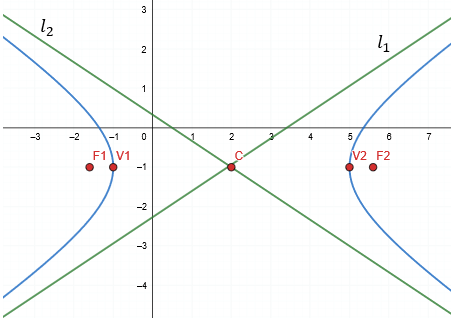
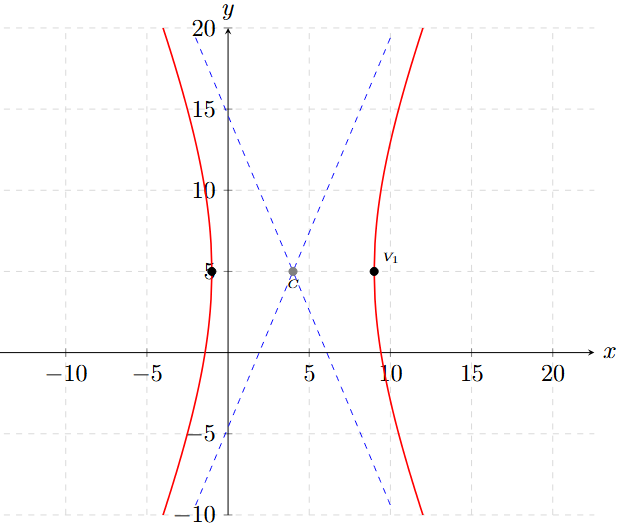
• Vértices \(V(2 \pm 3, -1) \rightarrow V_1(-1, -1), V_2(5, -1)\)
• Focos \(F(2 \pm 3.6, -1) \rightarrow F_1(-1.6, -1), F_2(5.6, -1)\)
Gráfica:
Ejemplo 2: Hipérbola Vertical (Paso a Paso)
Dada la ecuación \(9y^2 - 4x^2 - 54y + 16x + 29 = 0\), convertirla a su forma canónica y determinar las coordenadas de sus focos.
Solución:
Este ejercicio es interesante porque el término \(y^2\) es el positivo. Sigamos el proceso de completación de cuadrados:
1. Agrupamos (primero las \(y\) porque son positivas):
\[ (9y^2 - 54y) - (4x^2 - 16x) = -29 \]
2. Factorizamos:
\[ 9(y^2 - 6y) - 4(x^2 - 4x) = -29 \]
3. Completamos cuadrados:
\[ 9(y^2 - 6y + 9) - 4(x^2 - 4x + 4) = -29 + 9(9) - 4(4) \]
\[ 9(y-3)^2 - 4(x-2)^2 = -29 + 81 - 16 \]
\[ 9(y-3)^2 - 4(x-2)^2 = 36 \]
4. Dividimos entre 36:
\[ \frac{9(y-3)^2}{36} - \frac{4(x-2)^2}{36} = 1 \Rightarrow \frac{(y-3)^2}{4} - \frac{(x-2)^2}{9} = 1 \]
Tenemos una Hipérbola Vertical (la \(y\) manda).
• Centro: \(C(2, 3)\)
• \(a^2 = 4 \Rightarrow a=2\)
• \(b^2 = 9 \Rightarrow b=3\)
• Distancia focal \(c = \sqrt{4+9} = \sqrt{13} \approx 3.6\)
Coordenadas de los Focos:
Al ser vertical, el cambio es en la coordenada \(k\).
\[ F(h, k \pm c) \rightarrow F(2, 3 \pm \sqrt{13}) \]
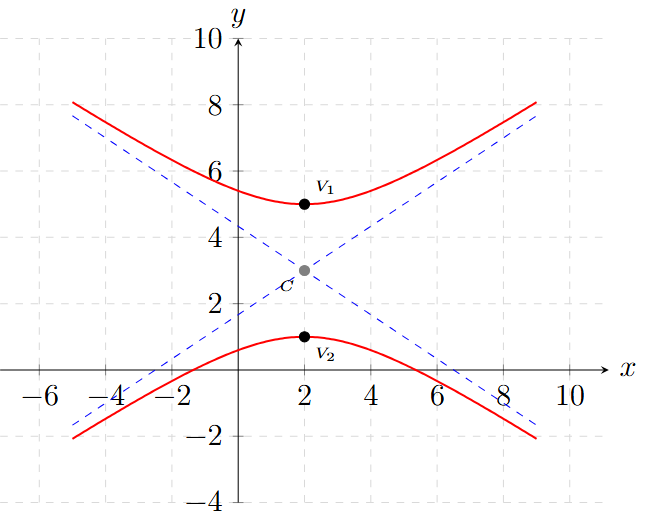
Ejemplo 3: Hallar la Ecuación dados los Vértices y Focos
Hallar la ecuación de la hipérbola cuyos vértices son \(V(2, 6)\) y \(V(2, -2)\), y cuyos focos son \(F(2, 7)\) y \(F(2, -3)\).
Solución:
Este es un problema de construcción inversa. Analicemos las coordenadas:
1. Identificar Orientación:
Observamos que la coordenada \(x\) no cambia (es siempre 2). La variación está en \(y\). Por lo tanto, el eje focal es Vertical.
2. Encontrar el Centro:
El centro es el punto medio entre los vértices (o los focos).
\[ C = \left( \frac{2+2}{2}, \frac{6+(-2)}{2} \right) = (2, 2) \]
Por tanto, \(h=2, k=2\).
3. Calcular \(a\) y \(c\):
• \(a\) es la distancia del centro al vértice: De \(y=2\) a \(y=6\), hay 4 unidades. (\(a=4\)).
• \(c\) es la distancia del centro al foco: De \(y=2\) a \(y=7\), hay 5 unidades. (\(c=5\)).
4. Calcular \(b\):
Usamos Pitágoras \(c^2 = a^2 + b^2\):
\[ 25 = 16 + b^2 \Rightarrow b^2 = 9 \]
5. Sustituir en la fórmula vertical:
\[ \frac{(y-2)^2}{16} - \frac{(x-2)^2}{9} = 1 \]
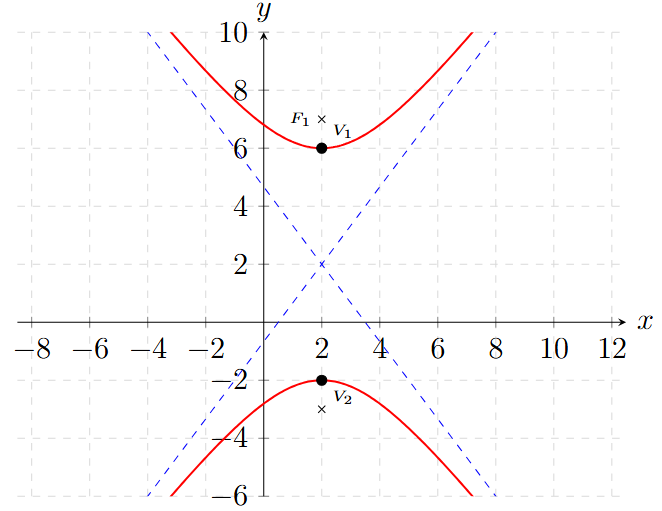
💡 Dato Curioso
Las asíntotas son las "guías invisibles" de la hipérbola. La curva se acerca infinitamente a ellas pero ¡jamás las toca! En el ejemplo anterior, las pendientes de estas líneas serían \(m = \pm a/b = \pm 4/3\).
Ejemplo 4: Obteniendo las Asíntotas
Dada la hipérbola \(\frac{(x+1)^2}{16} - \frac{(y-2)^2}{9} = 1\), determinar las ecuaciones de sus asíntotas.
Solución:
Primero identificamos los elementos:
• Es Horizontal (la \(x\) es positiva).
• \(a^2=16 \Rightarrow a=4\)
• \(b^2=9 \Rightarrow b=3\)
• Centro \(C(-1, 2)\)
La fórmula para las asíntotas de una hipérbola horizontal es:
\[ y - k = \pm \frac{b}{a}(x - h) \]
Sustituimos:
\[ y - 2 = \pm \frac{3}{4}(x + 1) \]
Esto nos da dos ecuaciones. Desarrollemos la primera (con signo positivo):
\[ 4(y - 2) = 3(x + 1) \]
\[ 4y - 8 = 3x + 3 \Rightarrow 3x - 4y + 11 = 0 \]
Ahora con signo negativo:
\[ 4(y - 2) = -3(x + 1) \]
\[ 4y - 8 = -3x - 3 \Rightarrow 3x + 4y - 5 = 0 \]
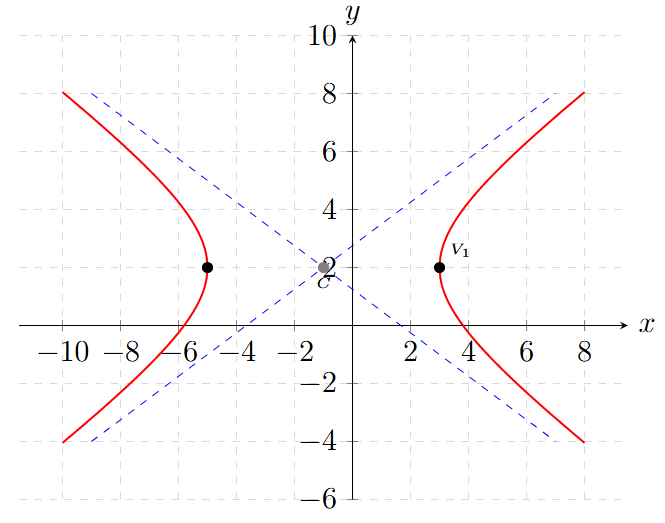
Ejemplo 5: Desafío de Ingeniería
Un arquitecto diseña una estructura hiperbólica. Si la "cintura" (eje transverso) más estrecha mide 10 metros y la distancia entre los focos es de 26 metros, determine la ecuación asumiendo el centro en \((4,5)\) y eje horizontal.
Solución:
Traduzcamos el lenguaje técnico a variables matemáticas:
- "Cintura más estrecha" se refiere a la longitud del Eje Transverso (\(2a\)).
\[ 2a = 10 \Rightarrow a = 5 \] - "Distancia entre focos" es \(2c\).
\[ 2c = 26 \Rightarrow c = 13 \] - Centro \(C(4,5)\).
Necesitamos \(b\) para la ecuación. Despejamos de la fórmula \(c^2 = a^2 + b^2\):
\[ 169 = 25 + b^2 \Rightarrow b^2 = 144 \]
Al ser eje horizontal, la ecuación queda:
\[ \frac{(x-4)^2}{25} - \frac{(y-5)^2}{144} = 1 \]
Ejemplo 6: Calculando Excentricidad y Lado Recto
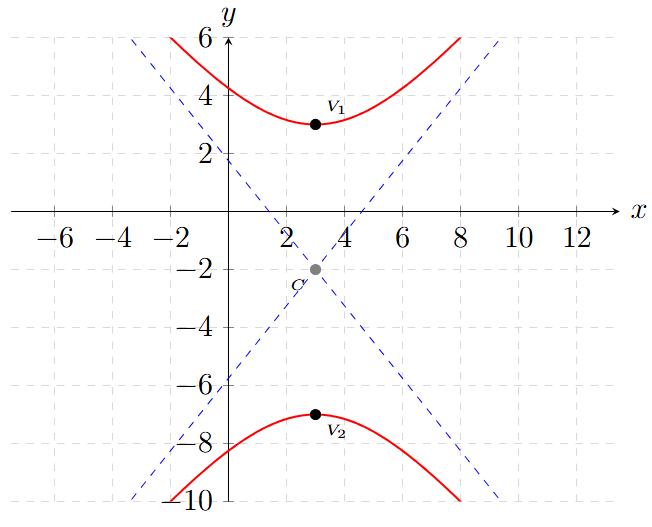
Dada la hipérbola vertical \(\frac{(y+2)^2}{25} - \frac{(x-3)^2}{16} = 1\), calcular su excentricidad y la longitud de su lado recto.
Solución:
Estos parámetros nos ayudan a entender qué tan "abierta" o "cerrada" es la hipérbola. Primero extraemos los valores básicos:
1. Identificar parámetros:
• \(a^2 = 25 \Rightarrow a = 5\)
• \(b^2 = 16 \Rightarrow b = 4\)
2. Calcular \(c\) (Distancia focal):
Usamos Pitágoras:
\[ c = \sqrt{a^2 + b^2} = \sqrt{25 + 16} = \sqrt{41} \approx 6.4 \]
3. Cálculo de la Excentricidad (\(e\)):
La excentricidad indica la curvatura. En la hipérbola siempre debe ser mayor a 1.
\[ e = \frac{c}{a} = \frac{\sqrt{41}}{5} \approx 1.28 \]
Como \(1.28 > 1\), el dato es coherente.
4. Cálculo del Lado Recto (\(LR\)):
Es la cuerda que pasa por el foco, perpendicular al eje focal.
\[ LR = \frac{2b^2}{a} \]
Sustituimos:
\[ LR = \frac{2(16)}{5} = \frac{32}{5} = 6.4 \]
Esto significa que el ancho de la hipérbola a la altura del foco es de 6.4 unidades.
Ejemplo 7: Hallar Ecuación dado Centro, Foco y Excentricidad
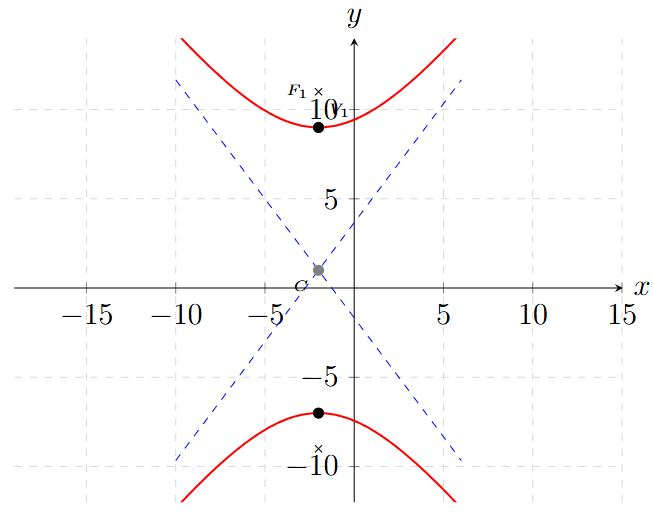
Determinar la ecuación de la hipérbola con centro en \(C(-2, 1)\), uno de sus focos en \(F(-2, 11)\) y excentricidad \(e = \frac{5}{4}\).
Solución:
Este es un problema clásico de examen donde debemos conectar los puntos.
1. Determinar Orientación:
Comparamos el Centro \((-2, 1)\) con el Foco \((-2, 11)\).
La coordenada \(x\) no cambia, pero la \(y\) sí. Esto nos grita que es una Hipérbola Vertical.
2. Calcular \(c\):
La distancia del Centro al Foco es \(c\).
\[ c = |11 - 1| = 10 \]
3. Despejar \(a\) de la Excentricidad:
Sabemos que \(e = \frac{c}{a}\). Sustituimos los datos que tenemos:
\[ \frac{5}{4} = \frac{10}{a} \]
Despejamos \(a\):
\[ 5a = 40 \Rightarrow a = \frac{40}{5} = 8 \]
4. Calcular \(b\):
Usamos la relación fundamental \(c^2 = a^2 + b^2\):
\[ 10^2 = 8^2 + b^2 \]
\[ 100 = 64 + b^2 \Rightarrow b^2 = 36 \]
5. Armar la Ecuación:
Al ser vertical, el término positivo es el de \(y\).
\[ \frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1 \]
Sustituyendo \(C(-2, 1)\), \(a^2=64\) y \(b^2=36\):
\[ \frac{(y-1)^2}{64} - \frac{(x+2)^2}{36} = 1 \]
📝 Ejercicios Propuestos
¿Listo para ponerte a prueba? Resuelve los siguientes problemas antes de ver la solución.
Problema Propuesto 1
Encuentra las coordenadas del centro y vértices de: \(\frac{(y+3)^2}{36} - \frac{(x-1)^2}{64} = 1\).
Ver Solución
Es vertical.
Centro: \(C(1, -3)\).
\(a = 6\).
Vértices: \(V(1, -3 \pm 6)\) → \(V_1(1, 3)\) y \(V_2(1, -9)\).
Problema Propuesto 2
Determina la ecuación general de una hipérbola con centro en \((1,1)\), \(a=3\), \(b=4\) y eje focal horizontal.
Ver Solución
Fórmula: \(\frac{(x-1)^2}{9} - \frac{(y-1)^2}{16} = 1\).
Multiplicando por 144: \(16(x-1)^2 - 9(y-1)^2 = 144\).
Desarrollando: \(16(x^2-2x+1) - 9(y^2-2y+1) - 144 = 0\).
Ecuación General: \(16x^2 - 9y^2 - 32x + 18y - 137 = 0\).
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado la Hipérbola con Centro Fuera del Origen.
Este tema es una pieza clave de nuestro artículo pilar sobre Geometría Analítica. Te recomendamos visitarlo para ver cómo este conocimiento se conecta con la Parábola y la Elipse.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
eso esta mal no. el resultado de la suma no es 36 el resultado de multiplicar 4 (4) =16 + 9 (1) =9 entonces 16+9=25 + 29 q nos da la ecuación hace un total de 54
-
Sólo para corregir, que en la ecuación se añadió un -9 en el término de la derecha, porque en la izquierda para completar el trinomio cuadrado se aumentó -1 que al multiplicar por 9 se convierte en -9. En la operación de la derecha quedaría 29+16-9, lo cual da efectivamente 36.
5 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar