Ecuación de la Parábola con Vértice fuera del Origen
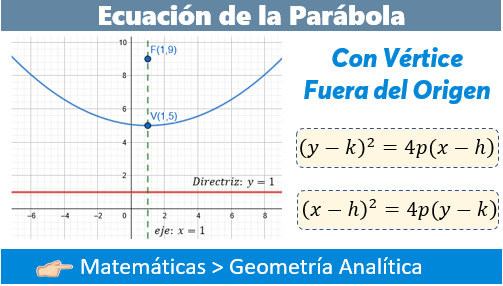
Después de haber dominado el caso de la parábola con vértice en el origen, es momento de subir de nivel. Ahora toca el estudio de la ecuación de la parábola con vértice fuera del origen. No te asustes, aunque suena más complejo, en realidad es muy sencillo si entendemos que simplemente hemos "movido" la figura de lugar en el plano cartesiano.
En este artículo, vamos a desglosar paso a paso cómo identificar, graficar y calcular estas ecuaciones. Pero antes, repasemos lo fundamental.
💡 ¡Ojo con el vocabulario!
Es muy común buscar en Google "parábola con centro fuera del origen", pero recuerda: las parábolas NO tienen centro (a diferencia del círculo o la elipse). Tienen un Vértice. Así que hablaremos siempre de \( V(h, k) \).
Elementos y Ecuación de la Parábola con Vértice (h, k)
Las parábolas se caracterizan por elementos clave: un vértice, un foco, una directriz, un lado recto y su concavidad. Cuando el vértice se mueve del origen \( (0,0) \), adquiere nuevas coordenadas que llamaremos (h, k).
- h: Representa el desplazamiento en el eje X.
- k: Representa el desplazamiento en el eje Y.
1. Parábola Horizontal con Vértice (h, k)
Observa la siguiente gráfica. Aquí la parábola está "acostada" y su eje de simetría es paralelo al eje X.
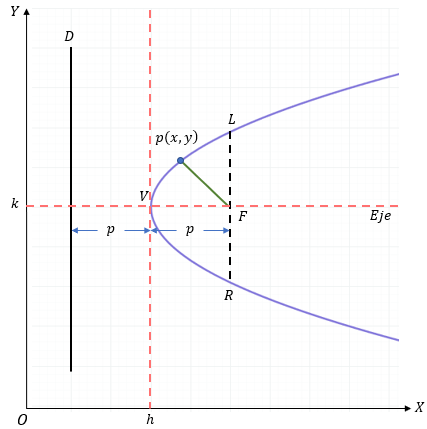
Fórmulas para el caso Horizontal
La característica principal es que la variable \( y \) es la que está elevada al cuadrado.
Ecuación Ordinaria:
\[ (y - k)^2 = 4p(x - h) \]
Elementos:
- Vértice: \( V(h,k) \)
- Foco: \( F(h+p, k) \)
- Directriz: \( x = h - p \)
- Ecuación del eje: \( y = k \)
- Lado Recto: \( LR = |4p| \)
⚠️ Sobre la Concavidad
El signo de p (parámetro) nos dice hacia dónde abre:
- Si \( p > 0 \): Abre a la Derecha.
- Si \( p < 0 \): Abre a la Izquierda.
2. Parábola Vertical con Vértice (h, k)
Este es el caso más común en física (tiro parabólico). Observa la gráfica:
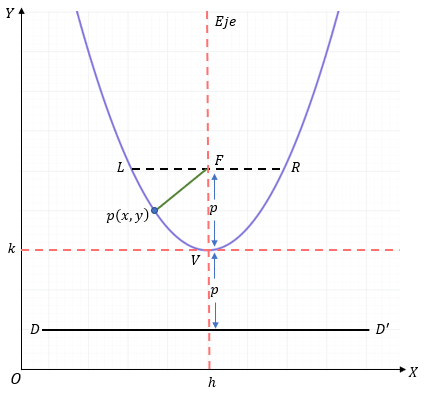
Fórmulas para el caso Vertical
Aquí, la variable \( x \) es la que está elevada al cuadrado.
Ecuación Ordinaria:
\[ (x - h)^2 = 4p(y - k) \]
Elementos:
- Vértice: \( V(h,k) \)
- Foco: \( F(h, k+p) \)
- Directriz: \( y = k - p \)
- Ecuación del eje: \( x = h \)
- Lado Recto: \( LR = |4p| \)
¿Qué es la Ecuación General?
A veces los ejercicios no piden la forma ordinaria (con paréntesis), sino la General. Esta se obtiene desarrollando los binomios al cuadrado e igualando a cero:
Horizontal: \( Cy^2 + Dx + Ey + F = 0 \)
Vertical: \( Ax^2 + Dx + Ey + F = 0 \)
Ejercicios Resueltos paso a paso
Vamos a poner en práctica la teoría. Analiza con cuidado cómo identificamos los datos en cada problema.
Ejemplo 1: Encontrar la Ecuación General dados dos puntos
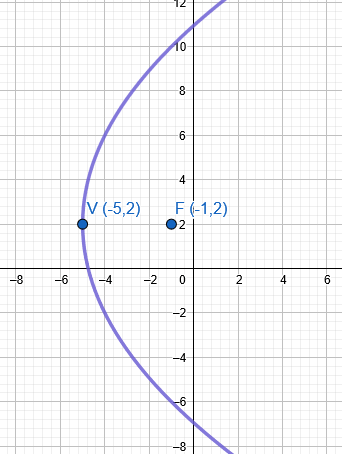
Determina la ecuación general de la parábola cuyo vértice y foco son los puntos (-5, 2) y (-1, 2) respectivamente.
Solución:
Lo primero y más recomendable es graficar (aunque sea un boceto rápido) para entender la orientación de la parábola.
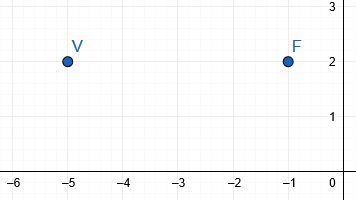
Al ver la imagen o analizar las coordenadas, notamos que:
- El eje focal es paralelo al eje X (porque la coordenada \( y=2 \) no cambia).
- El foco está a la derecha del vértice.
¡Es una parábola Horizontal que abre a la derecha!
Paso 1: Identificar h, k y p.
Del vértice \( V(-5, 2) \) sabemos que:
\[ h = -5, \quad k = 2 \]
La distancia del vértice al foco es el parámetro \( p \):
\[ p = -1 - (-5) = -1 + 5 = 4 \]
Entonces \( p = 4 \).
Paso 2: Sustituir en la fórmula ordinaria.
\[ (y - k)^2 = 4p(x - h) \]
\[ (y - 2)^2 = 4(4)(x - (-5)) \]
\[ (y - 2)^2 = 16(x + 5) \]
Paso 3: Desarrollar para llegar a la General.
Desarrollamos el binomio al cuadrado y multiplicamos el lado derecho:
\[ y^2 - 4y + 4 = 16x + 80 \]
Igualamos a cero pasando todo a la izquierda:
\[ y^2 - 4y + 4 - 16x - 80 = 0 \]
Ordenamos y simplificamos:
Resultado:
\[ y^2 - 4y - 16x - 76 = 0 \]
Aquí tienes la gráfica final de la parábola que acabamos de calcular:
Ejemplo 2: De Ecuación General a Elementos
Determina los elementos de la parábola (vértice, foco, directriz, eje y lado recto) y grafica la ecuación:
\[ x^2 - 2x - 16y + 81 = 0 \]
Solución:
Aquí tenemos que hacer ingeniería inversa. Observa que el término al cuadrado es la \( x \). Esto nos grita que es una parábola Vertical.
Paso 1: Agrupar términos.
Dejamos las \( x \) a la izquierda y pasamos las \( y \) y números a la derecha:
\[ x^2 - 2x = 16y - 81 \]
Paso 2: Completar el Trinomio Cuadrado Perfecto (TCP).
Este paso es vital. Tomamos el número que acompaña a la \( x \) lineal (que es 2), lo dividimos entre 2 y elevamos al cuadrado: \( (2/2)^2 = 1 \). Sumamos este 1 en ambos lados:
\[ x^2 - 2x + \mathbf{1} = 16y - 81 + \mathbf{1} \]
Factorizamos el lado izquierdo y simplificamos el derecho:
\[ (x - 1)^2 = 16y - 80 \]
Paso 3: Factorizar para obtener 'p'.
Factorizamos el 16 del lado derecho:
\[ (x - 1)^2 = 16(y - 5) \]
Ahora comparamos con la fórmula \( (x-h)^2 = 4p(y-k) \):
- \( h = 1 \)
- \( k = 5 \)
- \( 4p = 16 \rightarrow p = 4 \)
Paso 4: Calcular Elementos.
a) Vértice \( V(h,k) \):
\[ V(1, 5) \]
b) Foco \( F(h, k+p) \):
\[ F(1, 5+4) = F(1, 9) \]
c) Directriz \( y = k - p \):
\[ y = 5 - 4 = 1 \rightarrow y = 1 \]
d) Lado Recto \( |4p| \):
\[ LR = 16 \]
e) Gráfica:
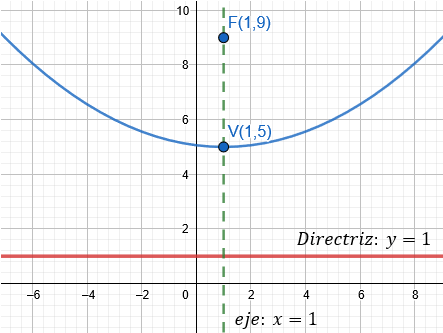
Ejemplo 3: General a Ordinaria (Caso Horizontal)
Dada la ecuación general de la parábola \( y^2 - 8y - 8x + 24 = 0 \), determina sus coordenadas del vértice, foco y valor del lado recto.
Solución:
Análisis: Observamos que el término cuadrático es \( y^2 \). Esto nos confirma que es una parábola Horizontal.
Paso 1: Agrupar términos.
Dejamos las "y" a la izquierda y pasamos las "x" y los independientes a la derecha:
\[ y^2 - 8y = 8x - 24 \]
Paso 2: Completar el Trinomio (TCP).
Tomamos el coeficiente lineal de y (-8), lo dividimos entre 2 y elevamos al cuadrado:
\[ \left(\frac{-8}{2}\right)^2 = (-4)^2 = 16 \]
Sumamos 16 en ambos lados de la ecuación:
\[ y^2 - 8y + \mathbf{16} = 8x - 24 + \mathbf{16} \]
Paso 3: Factorizar.
El lado izquierdo se convierte en binomio al cuadrado y simplificamos el derecho:
\[ (y - 4)^2 = 8x - 8 \]
Ahora factorizamos el 8 del lado derecho para dejar la x sola:
\[ (y - 4)^2 = 8(x - 1) \]
Paso 4: Extraer elementos.
Comparando con \( (y-k)^2 = 4p(x-h) \):
\[ V(h, k) \rightarrow V(1, 4) \]
\[ 4p = 8 \rightarrow p = 2 \]
- Vértice: \( V(1, 4) \)
- Foco \( (h+p, k) \): \( F(1+2, 4) \rightarrow F(3, 4) \)
- Lado Recto \( |4p| \): 8 unidades.
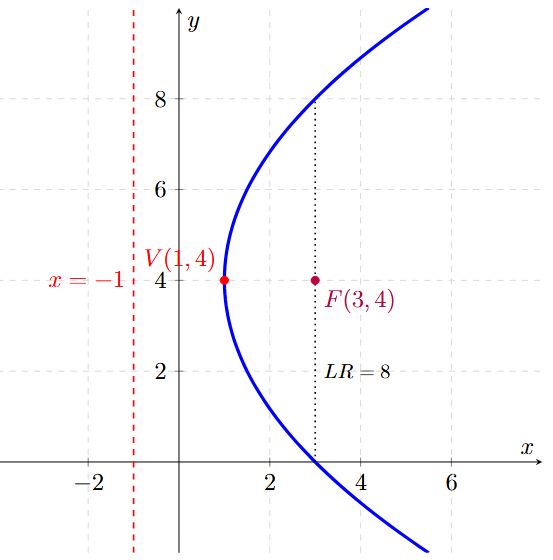
Ejemplo 4: Conociendo Vértice y Directriz
Halla la ecuación de la parábola cuyo vértice está en \( V(-2, 3) \) y su directriz es la recta \( x = -5 \).
Solución:
Este es un problema trampa común. Muchos estudiantes no saben si la parábola es vertical u horizontal. La clave está en la directriz.
Paso 1: Determinar la orientación.
La directriz es \( x = -5 \). Como es una línea de la forma "x = constante", es una recta vertical. Por definición, la parábola siempre es perpendicular a su directriz, así que esta parábola debe ser Horizontal.
Paso 2: Calcular el parámetro p.
La distancia del vértice a la directriz es \( p \).
Sabemos que la directriz está en \( x = -5 \) y el vértice en \( x = -2 \).
Si dibujamos esto mentalmente, la directriz está a la IZQUIERDA del vértice. Por lo tanto, la parábola debe abrir hacia la DERECHA (alejándose de la directriz).
\[ p = \text{Distancia} = -2 - (-5) = 3 \]
Como abre a la derecha, \( p \) es positivo: \( p = 3 \).
Paso 3: Ecuación.
Usamos la forma horizontal:
\[ (y - k)^2 = 4p(x - h) \]
\[ (y - 3)^2 = 4(3)(x - (-2)) \]
\[ (y - 3)^2 = 12(x + 2) \]
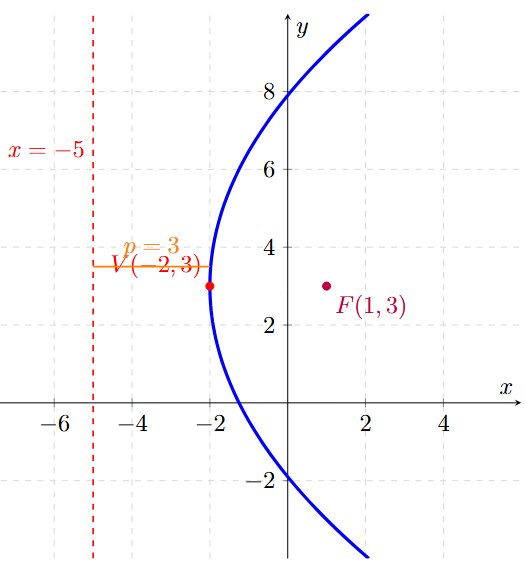
Ejemplo 5: Parábola que pasa por un punto específico
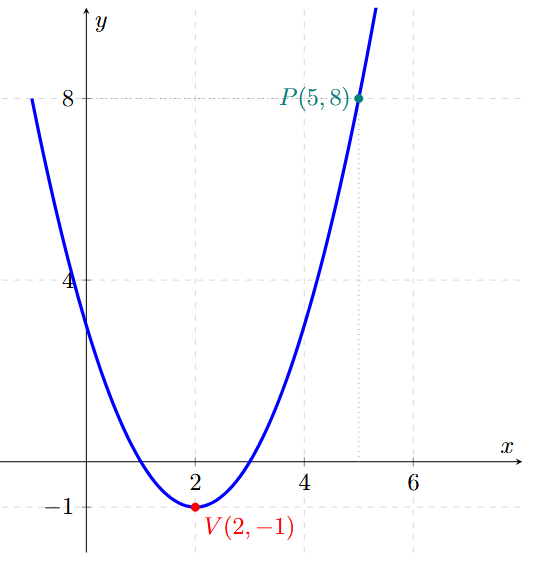
Una parábola tiene su vértice en \( V(2, -1) \), su eje es paralelo al eje Y, y pasa por el punto \( P(5, 8) \). Hallar su ecuación ordinaria.
Solución:
Aquí no nos dan el foco ni el parámetro \( p \). Tenemos que encontrarlo usando el punto por donde pasa la curva.
Paso 1: Elegir la fórmula correcta.
El problema dice "eje paralelo al eje Y", por lo tanto es Vertical:
\[ (x - h)^2 = 4p(y - k) \]
Paso 2: Sustituir Vértice y Punto.
Sustituimos \( h=2, k=-1 \) y usamos las coordenadas del punto \( P(5, 8) \) como \( x \) e \( y \) temporalmente para despejar \( p \).
\[ (5 - 2)^2 = 4p(8 - (-1)) \]
\[ (3)^2 = 4p(9) \]
\[ 9 = 36p \]
Paso 3: Despejar p.
\[ p = \frac{9}{36} = \frac{1}{4} \]
Paso 4: Ecuación Final.
Ahora que tenemos \( p \), escribimos la ecuación dejando x e y como variables:
\[ (x - 2)^2 = 4(\frac{1}{4})(y + 1) \]
Simplificando \( 4 \times \frac{1}{4} = 1 \):
Resultado: \( (x - 2)^2 = y + 1 \)
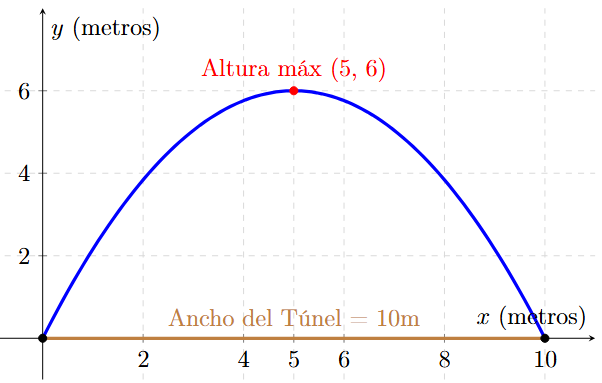
Ejemplo 6: Aplicación en la Vida Real (El Túnel)
Un túnel con forma de arco parabólico tiene una altura máxima de 6 metros y una anchura al nivel del suelo de 10 metros. Si situamos el origen de coordenadas en el extremo izquierdo de la base del túnel, determina la ecuación de la parábola.
Solución:
Este problema es excelente para entender la utilidad de las matemáticas. Vamos a modelarlo.
Paso 1: Coordenadas Clave.
Si el origen está en el extremo izquierdo de la base (0,0):
- El túnel empieza en \( (0,0) \) y termina en \( (10,0) \) (porque mide 10m de ancho).
- El punto más alto (Vértice) está justo a la mitad de la base (x=5) y a una altura de 6m.
- Por lo tanto, el Vértice es \( V(5, 6) \).
Paso 2: Tipo de Parábola.
Es un arco hacia abajo, así que es Vertical y \( p \) será negativo.
Paso 3: Calcular p usando un punto conocido.
Usamos la ecuación vertical \( (x - h)^2 = 4p(y - k) \).
Sustituimos el vértice \( V(5,6) \):
\[ (x - 5)^2 = 4p(y - 6) \]
Ahora, usamos un punto por donde pasa, por ejemplo, el origen \( (0,0) \):
\[ (0 - 5)^2 = 4p(0 - 6) \]
\[ 25 = 4p(-6) \]
\[ 25 = -24p \]
\[ p = -\frac{25}{24} \]
Paso 4: Ecuación del Túnel.
\[ (x - 5)^2 = 4(-\frac{25}{24})(y - 6) \]
Simplificando el 4 y el 24:
\[ (x - 5)^2 = -\frac{25}{6}(y - 6) \]
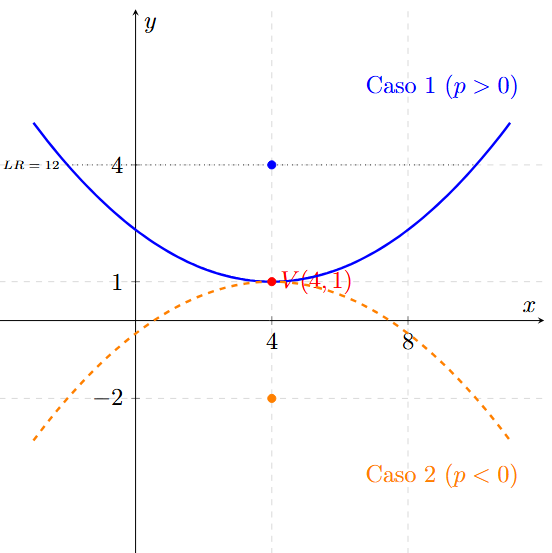
Ejemplo 7: El caso de las Dos Soluciones
Hallar la ecuación de la parábola cuyo eje es vertical, su vértice es \( V(4, 1) \) y la longitud de su lado recto es 12.
Solución:
¡Cuidado aquí! El problema nos da el tamaño de la apertura (Lado Recto), pero no nos dice si abre hacia arriba o hacia abajo. En matemáticas, esto significa que existen dos posibles soluciones.
Datos:
\( LR = |4p| = 12 \)
De aquí deducimos que \( 4p \) puede ser \( 12 \) o \( -12 \).
Caso 1: Abre hacia Arriba (p positivo).
\[ (x - 4)^2 = 12(y - 1) \]
Caso 2: Abre hacia Abajo (p negativo).
\[ (x - 4)^2 = -12(y - 1) \]
Ambas ecuaciones son respuestas válidas y correctas para el enunciado del problema.
Reto de Aprendizaje: ¡Ahora te toca a ti!
¿Listo para demostrar lo que aprendiste? 😎
Problema Propuesto 3
Hallar la ecuación ordinaria de la parábola cuyo vértice es el punto (3, 4) y cuyo foco es el punto (3, 2). Hallar también la ecuación de su directriz y la longitud de su lado recto.
Haz clic aquí para ver la solución explicada
Análisis: Como la coordenada X no cambia (3), es Vertical. Como el foco (2) está "abajo" del vértice (4), abre hacia abajo (p será negativa).
Cálculo de p:
\[ p = y_F - y_V = 2 - 4 = -2 \]
Ecuación Ordinaria:
\[ (x - 3)^2 = 4(-2)(y - 4) \]
\[ (x - 3)^2 = -8(y - 4) \]
Directriz:
\[ y = k - p = 4 - (-2) = 6 \]
\[ y = 6 \]
Lado Recto:
\[ LR = |4(-2)| = |-8| = 8 \]
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has completado el estudio de la Parábola Fuera del Origen.
Este tema es fundamental para comprender secciones cónicas más avanzadas. Te invitamos a visitar nuestra sección completa para seguir aprendiendo:
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
En el ejercicio No. 2 el parrafo donde dice solución. habla de un termino cuadrático en Y y debe decir en "X" y la parabola es vertical no horizontal.
La solución esta correcta. -
me gusta los ejercicios
-
Hola, muy buena explicación sobre la parábola, sin embargo en la solución del ejemplo 2 es un error decir que el termino cuadrático se tiene en "y" y que se trata de una parábola horizontal, realmente el termino cuadrático esta en "x" y corresponde a una parábola vertical, lo que se verifica en el transcurso de la resolución.
Saludos,
Diego
-
En el ejercicio 2 se equivocó en los valores de h y k. Es al revés de como están puestos en el ejemplo, favor de solucionar
-
Excelente material. Gracias por compartirlo y nuevamente gracias y felicidades por los ejemplos ilustrativos
15 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar