Potencia Eléctrica y Ley de Watt: Fórmulas y 20 Ejercicios [PDF]

Cuando compras un foco LED de 10 Watts o un cargador de carga rápida de 60 Watts, estás hablando de Potencia Eléctrica. Este concepto es fundamental para entender cuánto "trabajo" puede hacer un aparato y, más importante aún, cuánto te va a costar en tu recibo de luz.

En este artículo aprenderás a usar las fórmulas de la Ley de Watt, a calcular el consumo en Kilowatt-hora (kWh) y resolveremos problemas típicos de examen.

¿Qué es la Potencia Eléctrica?

La potencia eléctrica se define como la cantidad de energía que consume (o entrega) un dispositivo eléctrico por unidad de tiempo. Su unidad de medida en el Sistema Internacional es el Watt (W).

La Ley de Watt

A menudo escucharás hablar de la "Ley de Watt". Esta ley establece que la potencia eléctrica es directamente proporcional al voltaje y a la corriente que circula por un circuito.

Donde:

• P = Potencia Eléctrica [Watts, W]
• V = Voltaje [Volts, V]
• I = Intensidad de Corriente [Amperes, A]

Triángulo de la Ley de Watt

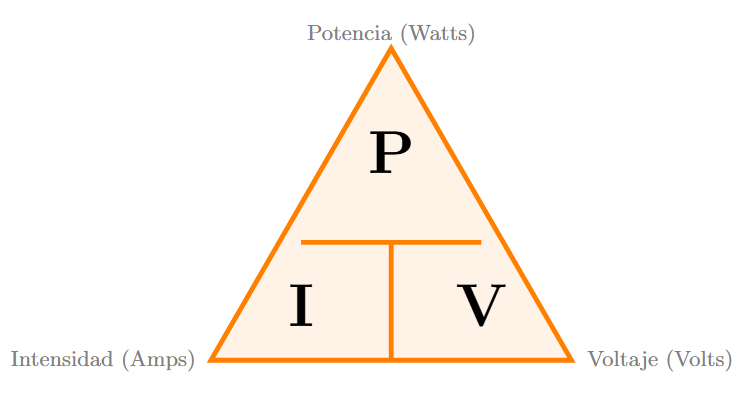
Al igual que con la Ley de Ohm, podemos usar un triángulo para facilitar los despejes:

• Para calcular Potencia (P): \( V \cdot I \)
• Para calcular Corriente (I): \( P / V \)
• Para calcular Voltaje (V): \( P / I \)

Combinación con la Ley de Ohm (Fórmulas Extra)

Si combinamos la Ley de Watt (\(P=VI\)) con la Ley de Ohm (\(V=IR\)), obtenemos dos fórmulas muy útiles cuando no tenemos todos los datos:

1. Si no tenemos el Voltaje:

\[ P = (I \cdot R) \cdot I \Rightarrow P = I^2 \cdot R \]

2. Si no tenemos la Corriente:

\[ P = V \cdot \left( \frac{V}{R} \right) \Rightarrow P = \frac{V^2}{R} \]

✅ Ejercicios Resueltos de Potencia (Básicos)

Empecemos con aplicaciones directas de las fórmulas.

Solución:

Datos: \(V=150\text{ V}\), \(I=6\text{ A}\).

Usamos la fórmula directa:
\[ P = V \cdot I = (150\text{ V})(6\text{ A}) = 900\text{ W} \]

Resultado: 900 Watts.

Solución:

Datos: \(P=1500\text{ W}\), \(V=130\text{ V}\).

Despejamos \(I\) de \(P=VI\):

\[ I = \frac{P}{V} = \frac{1500\text{ W}}{130\text{ V}} = 11.53\text{ A} \]

Resultado: 11.53 Amperes.

Solución:

No tenemos el voltaje, así que usamos la fórmula con resistencia:

\[ P = I^2 \cdot R \]

\[ P = (6\text{ A})^2 \cdot (56\ \Omega) \]

\[ P = 36 \cdot 56 = 2016\text{ W} \]

Resultado: 2016 Watts (o 2.016 kW).

Solución:

Fórmula original: \( P = V^2 / R \).

Nueva Potencia (\(P'\)) con nuevo voltaje (\(V' = V/4\)):

\[ P' = \frac{(V/4)^2}{R} = \frac{V^2 / 16}{R} = \frac{1}{16} \left( \frac{V^2}{R} \right) \]

Como \( \frac{V^2}{R} \) es la potencia original \(P\):

\[ P' = \frac{1}{16} P \]

Resultado: La potencia se reduce a una dieciseisava parte.

Solución:

Tenemos \(P_{max} = 0.25\text{ W}\) y \(R = 100\ \Omega\).

Usamos la fórmula \( P = I^2 R \). Despejamos \(I\):

\[ I^2 = \frac{P}{R} \Rightarrow I = \sqrt{\frac{P}{R}} \]

\[ I = \sqrt{\frac{0.25}{100}} = \sqrt{0.0025} \]

\[ I = 0.05\text{ A} \]

Resultado: La corriente máxima es 0.05 Amperes (o 50 mA).

Solución:

Usamos \( P = \frac{V^2}{R} \). Despejamos la resistencia: \( R = \frac{V^2}{P} \).

Como el voltaje \(V\) es el mismo (120V) para ambos:

Resistencia Foco A (60W): \( R_A = \frac{120^2}{60} = \frac{14400}{60} = 240\ \Omega \)

Resistencia Foco B (100W): \( R_B = \frac{120^2}{100} = \frac{14400}{100} = 144\ \Omega \)

Resultado: El foco de 60 W tiene mayor resistencia (240 \(\Omega\)). A menor potencia, mayor resistencia (en paralelo).

Solución:

1. Corriente: \( I = P/V = 40/120 = 0.333\text{ A} \).

2. Resistencia: \( R = V/I = 120/0.333 = 360\ \Omega \).

(También podías usar \( R = V^2/P \)).

Resultado: 0.33 A y 360 Ohms.

✅ Ejercicios de Consumo y Costo Eléctrico (kWh)

Estos son los problemas más prácticos. La compañía de luz te cobra por Energía, no por potencia.

\[ E = P \cdot t \]

Donde la energía \(E\) se mide en Kilowatt-hora (kWh). Para esto, la potencia debe estar en kW y el tiempo en horas.

Solución:

Paso 1: Calcular Potencia

\[ P = V \cdot I = 120 \cdot 9 = 1080\text{ W} \]

Convertimos a Kilowatts (dividiendo entre 1000):

\[ P = 1.08\text{ kW} \]

Paso 2: Convertir tiempo a horas

\[ t = \frac{95\text{ min}}{60} = 1.583\text{ h} \]

Paso 3: Calcular Energía (a)

\[ E = P \cdot t = (1.08\text{ kW})(1.583\text{ h}) = 1.71\text{ kWh} \]

Paso 4: Calcular Costo (b)

\[ \text{Costo} = E \times \text{Precio} = 1.71 \times 2.8 = \$4.78 \]

Resultado: Consume 1.71 kWh y cuesta $4.78.

Solución:

Conversiones:

\( P = 90\text{ W} = 0.09\text{ kW} \)

\( t = 45\text{ min} = 0.75\text{ h} \)

Energía:

\[ E = 0.09 \cdot 0.75 = 0.0675\text{ kWh} \]

Costo:

\[ \text{Costo} = 0.0675 \times 2.5 = \$0.168 \]

Resultado: Cuesta aproximadamente 17 centavos.

Solución:

a) Energía Total:

Potencia en kW: \( 400\text{ W} = 0.4\text{ kW} \).

Horas totales al mes: \( 6 \text{ horas/día} \times 30 \text{ días} = 180 \text{ horas} \).
\[ E = P \cdot t = (0.4\text{ kW})(180\text{ h}) = 72\text{ kWh} \]

b) Costo:

\[ \text{Costo} = 72\text{ kWh} \times \$2.00 = \$144.00 \]

Resultado: Paga $144.00 al mes.

Solución:

Este es un problema de comparación.

1. Consumo Focos Viejos:

Potencia total: \( 5 \times 100\text{ W} = 500\text{ W} = 0.5\text{ kW} \).

Tiempo: \( 5 \text{ h/día} \times 60 \text{ días} = 300\text{ h} \).

Energía: \( 0.5 \times 300 = 150\text{ kWh} \).

Costo Viejo: \( 150 \times 1.5 = \$225 \).

2. Consumo Focos LED:

Potencia total: \( 5 \times 12\text{ W} = 60\text{ W} = 0.06\text{ kW} \).

Energía: \( 0.06 \times 300 = 18\text{ kWh} \).

Costo Nuevo: \( 18 \times 1.5 = \$27 \).

3. Ahorro:

\[ \text{Ahorro} = \$225 - \$27 = \$198 \]

Resultado: Se ahorran $198 cada bimestre.

Solución:

El error común es multiplicar por 24 horas. El problema ya nos da el tiempo efectivo.

Potencia: \( 0.3\text{ kW} \).

Tiempo total: \( 8 \text{ h/día} \times 60 \text{ días} = 480\text{ h} \).

\[ E = (0.3)(480) = 144\text{ kWh} \]

Resultado: Consume 144 kWh al bimestre.

Ejercicios Para Practicar

Intenta resolverlos antes de desplegar la solución.

Descargar Guía: 20 Ejercicios de Ley de Watt [PDF]

¿Necesitas ejercicios más difíciles o de circuitos mixtos? Descarga nuestra guía completa.

Conclusión

La potencia eléctrica es el puente entre la teoría de circuitos y el mundo real del consumo de energía. Recordar que \( P = VI \) te salvará en la mayoría de los casos, pero no olvides las variantes con resistencia para cuando te falten datos.