Dilatación Superficial - Ejercicios Resueltos
Ey ¡Qué tal!, Hace algunos meses publicábamos en el blog un tema relacionado a las diversas dilataciones, entre ellas mencionamos la dilatación lineal, pero quedaron varias dudas, ya que no se detallaban los demás casos de dilatación como la superficial y la volumétrica. Así que en este post hablaremos de la dilatación superficial. 😎
¿Qué es la dilatación Superficial?
La dilatación superficial es el incremento proporcional de área o superficie que experimenta cierto objeto con determinada sustancia, de área igual a la unidad, al elevarse su temperatura a un grado centígrado.
Este coeficiente muchos autores y libros le han denominado con la letra griega beta$\displaystyle \beta$ . El coeficiente de dilatación superficial se usa para los trabajos en sólidos, si se conoce el coeficiente de dilatación lineal de un sólido, entonces su coeficiente de dilatación superficial será dos veces mayor, por lo que tenemos la siguiente relación matemática:
$\displaystyle \beta =2\alpha $
Por ejemplo, si tenemos el coeficiente de dilatación lineal del cobre que es $\displaystyle 16.6x{{10}^{-6}}$ , por tanto, su coeficiente de dilatación superficial sería:
$\displaystyle \beta =2\alpha =2(16.6x{{10}^{-6}})=33.2x{{10}^{-6}}{}^\circ {{C}^{-1}}$
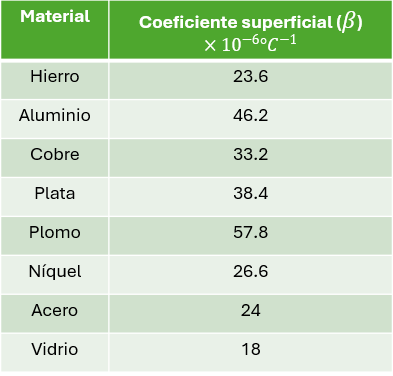
Bien, pero para no tener que calcular uno por uno, hemos elaborado una nueva tabla de algunos elementos con su dilatación superficial.
Tabla de Dilatación Superficial
Aquí tenemos la tabla de las sustancias de dilatación superficial que nos servirá para la resolución de ejemplos resueltos.
Al conocer el coeficiente de dilatación superficial de un objeto sólido, prácticamente podemos calcular el área final que tendrá al variar su temperatura conforme a la siguiente fórmula matemática de dilatación superficial.
Fórmula de la Dilatación Superficial
$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\beta({{T}_{f}}-{{T}_{0}}) \right]$
Dónde:
$\displaystyle {{A}_{f}}$ = Área final en unidades en metro cuadrado.
$\displaystyle {{A}_{0}}$ = Área inicial en unidades de metro cuadrado
$\displaystyle \beta$= Coeficiente de dilatación superficial
$\displaystyle {{T}_{f}}$= Temperatura final medida en grados Celcius (°C)
$\displaystyle {{T}_{0}}$= Temperatura inicial medida en grados Celcius (°C)
[alert-warning]En algunos ejercicios propuestos, la superficie se encuentra expresada en centímetros cuadrados, lo cual también es válido.[/alert-warning]
Ejercicios Resueltos de Dilatación Superficial
Bien, ningún problema en Física se puede entender sino se hace uso de los ejercicios. Así que llegó el momento de practicar.
Solución:
Bien, como siempre debemos considerar los datos que tenemos, y los implícitos, aquellos que no están en el problema pero que nos proporcionan pistas.
Sabemos que se trata de la sustancia del vidrio, por lo que debemos considerar su coeficiente de dilatación superficial, a su vez tenemos un área inicial de 1.4 metros cuadrados, y una variación de la temperatura inicial de 21°C hasta 35°C. Entonces la incógnita es el área final, variable que afortunadamente ya la tenemos despejada.
Si tienes problemas con el despeje, te recomendamos ver el artículo de como despejar fórmulas
$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\beta({{T}_{f}}-{{T}_{0}}) \right]$
Sustituimos nuestros datos en la fórmula
$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left[ {1+18x{{{10}}^{{-6}}}^{{}^\circ }{{C}^{{-1}}}\left( {{{{35}}^{{}^\circ }}C-{{{21}}^{{}^\circ }}C} \right)} \right]$
Luego
$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left[ {1+2.52\times {{{10}}^{{-6}}}} \right]$
Ahora realizamos la suma del paréntesis.
$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left( {1.000252} \right)$
Lo que nos da como resultado
Resultado:
$\displaystyle {{A}_{f}}=1.4003528{{m}^{2}}$
Solución:
Nuevamente en el problema nos piden el área final, por lo tanto seguiremos usando la misma fórmula que el ejercicio anterior, solamente debemos tener cuidado con nuestros datos, ya que sabemos que se trata de una puerta de aluminio, con ello ya tenemos el dato del coeficiente de dilatación superficial, nos hace falta área inicial, solamente. ¿Cómo la obtenemos?.
Pues fácilmente, sabemos que se trata de una puerta, así que calculemos el área por sus dimensiones a lo largo y ancho. Así que sería:
$\displaystyle {{A}_{0}}=(2.4m)(0.9m)=2.16{{m}^{2}}$
Una vez teniendo este dato, procedemos a sustituir en la fórmula. Pero claro, teniendo en cuenta el valor de el coeficiente de dilatación superficial.
$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\beta ({{T}_{f}}-{{T}_{0}}) \right]$
Ahora tenemos.
$\displaystyle {{A}_{f}}=2.16{{m}^{2}}\left[ 1+46.2x{{10}^{-6}}(23{}^\circ C-40{}^\circ C) \right]$
$\displaystyle {{A}_{f}}=2.16{{m}^{2}}\cdot 0.9992146$
Multiplicando tenemos.
Resultado:
$\displaystyle {{A}_{f}}=2.158303536{{m}^{2}}$
Qué sería nuestro resultado.
Ejercicios Para Practicar de Dilatación Superficial
Hemos colocado algunos ejercicios de dilatación superficial para que pueda ir mejorando y ampliando su conocimiento respecto al tema. Se incluye la solución de los ejercicios paso a paso, solamente de click en "Ver Solución".
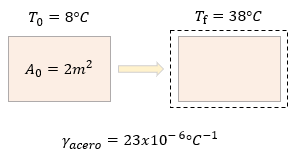
[alert-note] Problema 3. Una lámina de acero tiene un área de 2m² a una temperatura de 8°C ¿Cuál será su área final al elevarse su temperatura a 38°C? [/alert-note]
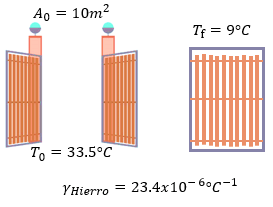
[alert-note] Problema 4. A una temperatura de 33.5°C un portón de hierro tiene un área de 10m². ¿Cuál será su área final al disminuir su temperatura a 9°C? [/alert-note]
[alert-note]Problema 5. En un laboratorio un científico estudia el fenómeno de dilatación, en su experimento desea encajar perfectamente un anillo de cobre en un cilindro. El anillo tiene un radio de 2cm a 20°C y un coeficiente de dilatación lineal de 17x10^(-6)°C ¯¹ ; determine a que temperatura el anillo debe ser calentado para que sea introducido en un cilindro cuya área de base es igual a 15cm², considere π = 3.14 [/alert-note]
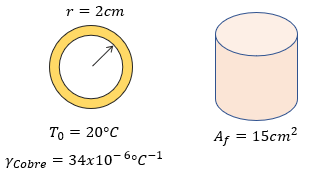
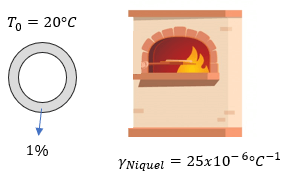
[alert-note]Problema 6. Una moneda fabricada con níquel puro, está a una temperatura ambiente de 20°C, al ser llevada a un horno, ella sufre un aumento del 1% en el área de su superficie. ¿Cuál es la temperatura del horno? , el coeficiente de dilatación superficial del níquel es de 25x10^(-6) °C ¯¹ [/alert-note]
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
una barra experimenta dilatacion consecuentemente su area o superficie varia en 0,00132m2 la barra posee un coeficiente de dilatacion beta igual a 2,2*10^-5 en las unidades respectivas la temperatura inicia fue de 8°C y la final fue 38°C ¿Calcular el valor del area inicial de la barra ?
ayuda con este problema porfavor -
una placa rectangular de zinc tiene 2ft de longitud y 40cm de ancho.cuando la temperatura es de 293.15 k.suponiendo que la placa es calentada hasta 248f cual sera el area final dela placa ft
-
Una placa de metal tiene las dimensiones de 10x10m cuando su temperatura es de 10°c se observa que cada lado aumenta 20m ¿cual es su coeficiente de dilatación superficial?
-
Un cuadrado de aluminio de 2m cuadrados de superficie se encuentra inicialmente a 10°c y se lo calienta hasta los 510°c. Calcular lo que se dilató esa superficie.
-
-
Cual es la ecuacion para hallar el coeficiente de dilatacion superficial?
-
No entiendo nada no seria mejor un video porfi
-
-
Cual seria el diametro de un anillo de concreto si un diámetro es de 2 m cuando la temperatura es de 25°C. ¿Cuál será su diámetro si la temperatura disminuye a 10°C? αconcreto = 0.7X10-5 °C-1
-
Ese es un ejercicio de dilatación lineal. No uno de área. la ecuación es similar.
-
2. Una ventana de vidrio tiene una superficie de 1.4 m2 cuando se encuentra a temperatura ambiente de 62.6 °F ¿Cual es el área final que logra aumentar la ventana cuando la temperatura se eleva a 46°C? me pueden ayudar
-
1.40059276 m2
-
Ese
-
1.40059276 m2 ese
-
ayuda a resover este problema
se desea revestir una pared de 7mt de frente por 9 metros de alto con piezas metálicas de aluminio de 0.3 X 15 X 25 cm3 considerando que el coeficiente de dilatación lineal del aluminio es 23X10 -6 ºC-1
determine cual debe ser el espacio entre las juntas de cada placa, si en el lugar donde se realizara la edificación se tiene una temperatura mínima de 44ºf y una máxima de 62ºf. durante el año
-
-
4._ A una temperatura de 22°C una ventana de vidrio tiene un área de 1.8 metros cuadrados. Cuál será su área final al aumentar su temperatura a 37 °C? .
-
Datos: Formula: Af=(1+y(Tf- To)
Af=1.8m2(1+(1.46x10elevado ala -6)(37ª-22ªc Af=1.80003942m cuadradosAo=1.8 m cuadrados
To=22ªc
Tf=37ªc
Af=?
a=7.3.x10elevado al exponente -6
y=2 a Y =2(7.3x10)
Y=1.46x10 -
Que superficie tenía a 10°C , una alambre de plomo que a 200°C alcanzó su superficie de 28.1 cm1
Es urgenteee xfisss
-
-
-
Una lámina de aluminio se eleva desde 20 cm hasta 70 CM la superficie inicial fue de 5 metros cuál calcular de la superficie final y la variación de superficie
-
-
1.98m
-
Una lámina de aluminio se eleva desde 20 C hasta 70 C la suoerficue eincial fue 5cm calcular la superficie final me ayudannn porfa
-
-
A la Placa de metal se le ha aplicado un orificio como muestra la figura. Hallar cuál será el área final de dicho orificio si calentamos a la placa en 10°. Considere 2.10^-4
-
Una plancha de acero tiene dimensiones 4m x 6m a 10°c. Si se calienta a 68°c, ¿Cual será su incremento de superficie?
Calcula el área de la plancha a 10°c
Determina el área de la plancha después de haber Sido calentada. Utiliza: S=s(1+ 2a∆t) y considera que a=12 X10 a la sexta°c
¿cuanto fue la variación del área de la plancha de acero?. Ayúdenme por favor. -
un dato esta erróneo recordando que el diámetro se obtiene mediante la formula πr² entonces el diámetro seria 2m² aplicando lo aprendido con dilatación superficial la respuesta es que disminuyo su area a = 1.99958m²
-
según mis cálculos da 1.99955m
-
4- Una ventana de vidrio tiene las siguientes dimensiones: 150 ×250 cm cuando la temperatura es de 10°C. ¿En cuánto aumenta su área cuando la temperatura se eleva a 40°C? Considera que el vidrio tiene espacio para dilatarse.
-
Dos baldosas cuadradas; una de aluminio cuya superficie es 1600cm2 y otra de hojalata cuya superficie es 2500cm2 estan dispuestas sobre el piso. Si estan separadas 0,2mm ¿cual debe ser la variacion de temperatura para que entren en contacto?
-
61 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar