Dilatación Superficial - Ejercicios Resueltos
Ey ¡Qué tal!, Hace algunos meses publicábamos en el blog un tema relacionado a las diversas dilataciones, entre ellas mencionamos la dilatación lineal, pero quedaron varias dudas, ya que no se detallaban los demás casos de dilatación como la superficial y la volumétrica. Así que en este post hablaremos de la dilatación superficial. 😎
¿Qué es la dilatación Superficial?
La dilatación superficial es el incremento proporcional de área o superficie que experimenta cierto objeto con determinada sustancia, de área igual a la unidad, al elevarse su temperatura a un grado centígrado.
Este coeficiente muchos autores y libros le han denominado con la letra griega beta$\displaystyle \beta$ . El coeficiente de dilatación superficial se usa para los trabajos en sólidos, si se conoce el coeficiente de dilatación lineal de un sólido, entonces su coeficiente de dilatación superficial será dos veces mayor, por lo que tenemos la siguiente relación matemática:
$\displaystyle \beta =2\alpha $
Por ejemplo, si tenemos el coeficiente de dilatación lineal del cobre que es $\displaystyle 16.6x{{10}^{-6}}$ , por tanto, su coeficiente de dilatación superficial sería:
$\displaystyle \beta =2\alpha =2(16.6x{{10}^{-6}})=33.2x{{10}^{-6}}{}^\circ {{C}^{-1}}$
Bien, pero para no tener que calcular uno por uno, hemos elaborado una nueva tabla de algunos elementos con su dilatación superficial.
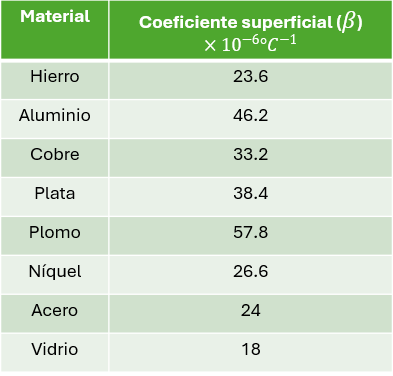
Tabla de Dilatación Superficial
Aquí tenemos la tabla de las sustancias de dilatación superficial que nos servirá para la resolución de ejemplos resueltos.
Al conocer el coeficiente de dilatación superficial de un objeto sólido, prácticamente podemos calcular el área final que tendrá al variar su temperatura conforme a la siguiente fórmula matemática de dilatación superficial.
Fórmula de la Dilatación Superficial
$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\beta({{T}_{f}}-{{T}_{0}}) \right]$
Dónde:
$\displaystyle {{A}_{f}}$ = Área final en unidades en metro cuadrado.
$\displaystyle {{A}_{0}}$ = Área inicial en unidades de metro cuadrado
$\displaystyle \beta$= Coeficiente de dilatación superficial
$\displaystyle {{T}_{f}}$= Temperatura final medida en grados Celcius (°C)
$\displaystyle {{T}_{0}}$= Temperatura inicial medida en grados Celcius (°C)
[alert-warning]En algunos ejercicios propuestos, la superficie se encuentra expresada en centímetros cuadrados, lo cual también es válido.[/alert-warning]
Ejercicios Resueltos de Dilatación Superficial
Bien, ningún problema en Física se puede entender sino se hace uso de los ejercicios. Así que llegó el momento de practicar.
Solución:
Bien, como siempre debemos considerar los datos que tenemos, y los implícitos, aquellos que no están en el problema pero que nos proporcionan pistas.
Sabemos que se trata de la sustancia del vidrio, por lo que debemos considerar su coeficiente de dilatación superficial, a su vez tenemos un área inicial de 1.4 metros cuadrados, y una variación de la temperatura inicial de 21°C hasta 35°C. Entonces la incógnita es el área final, variable que afortunadamente ya la tenemos despejada.
Si tienes problemas con el despeje, te recomendamos ver el artículo de como despejar fórmulas
$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\beta({{T}_{f}}-{{T}_{0}}) \right]$
Sustituimos nuestros datos en la fórmula
$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left[ {1+18x{{{10}}^{{-6}}}^{{}^\circ }{{C}^{{-1}}}\left( {{{{35}}^{{}^\circ }}C-{{{21}}^{{}^\circ }}C} \right)} \right]$
Luego
$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left[ {1+2.52\times {{{10}}^{{-6}}}} \right]$
Ahora realizamos la suma del paréntesis.
$\displaystyle {{A}_{f}}=1.4{{m}^{2}}\left( {1.000252} \right)$
Lo que nos da como resultado
Resultado:
$\displaystyle {{A}_{f}}=1.4003528{{m}^{2}}$
Solución:
Nuevamente en el problema nos piden el área final, por lo tanto seguiremos usando la misma fórmula que el ejercicio anterior, solamente debemos tener cuidado con nuestros datos, ya que sabemos que se trata de una puerta de aluminio, con ello ya tenemos el dato del coeficiente de dilatación superficial, nos hace falta área inicial, solamente. ¿Cómo la obtenemos?.
Pues fácilmente, sabemos que se trata de una puerta, así que calculemos el área por sus dimensiones a lo largo y ancho. Así que sería:
$\displaystyle {{A}_{0}}=(2.4m)(0.9m)=2.16{{m}^{2}}$
Una vez teniendo este dato, procedemos a sustituir en la fórmula. Pero claro, teniendo en cuenta el valor de el coeficiente de dilatación superficial.
$\displaystyle {{A}_{f}}={{A}_{0}}\left[ 1+\beta ({{T}_{f}}-{{T}_{0}}) \right]$
Ahora tenemos.
$\displaystyle {{A}_{f}}=2.16{{m}^{2}}\left[ 1+46.2x{{10}^{-6}}(23{}^\circ C-40{}^\circ C) \right]$
$\displaystyle {{A}_{f}}=2.16{{m}^{2}}\cdot 0.9992146$
Multiplicando tenemos.
Resultado:
$\displaystyle {{A}_{f}}=2.158303536{{m}^{2}}$
Qué sería nuestro resultado.
Ejercicios Para Practicar de Dilatación Superficial
Hemos colocado algunos ejercicios de dilatación superficial para que pueda ir mejorando y ampliando su conocimiento respecto al tema. Se incluye la solución de los ejercicios paso a paso, solamente de click en "Ver Solución".
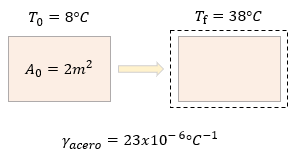
[alert-note] Problema 3. Una lámina de acero tiene un área de 2m² a una temperatura de 8°C ¿Cuál será su área final al elevarse su temperatura a 38°C? [/alert-note]
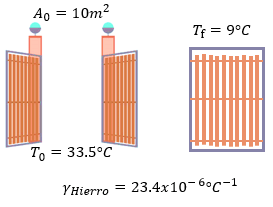
[alert-note] Problema 4. A una temperatura de 33.5°C un portón de hierro tiene un área de 10m². ¿Cuál será su área final al disminuir su temperatura a 9°C? [/alert-note]
[alert-note]Problema 5. En un laboratorio un científico estudia el fenómeno de dilatación, en su experimento desea encajar perfectamente un anillo de cobre en un cilindro. El anillo tiene un radio de 2cm a 20°C y un coeficiente de dilatación lineal de 17x10^(-6)°C ¯¹ ; determine a que temperatura el anillo debe ser calentado para que sea introducido en un cilindro cuya área de base es igual a 15cm², considere π = 3.14 [/alert-note]
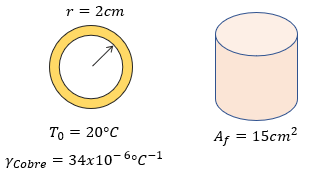
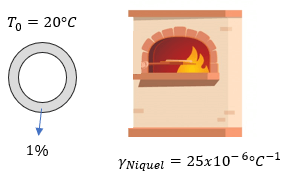
[alert-note]Problema 6. Una moneda fabricada con níquel puro, está a una temperatura ambiente de 20°C, al ser llevada a un horno, ella sufre un aumento del 1% en el área de su superficie. ¿Cuál es la temperatura del horno? , el coeficiente de dilatación superficial del níquel es de 25x10^(-6) °C ¯¹ [/alert-note]
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Ayuda¡¡¡¡¡
Una lamina rectangular de aluminio mide a 0 °C, 4 m de ancho y 6 m de largo ¿cual sera su superficie a 45 °C -
un tubo metalico mide 100mt de largo a 0ºc y 100ºc cual es su coeficiente de dilatacion lineal
-
Determinar el tiempo que tarda un móvil en recorrer 12 millas a una velocidad de 72km/hrs.
-
-
Ayuda por favor.....
Una lamina rectangular de aluminio mide a 0ºc 3mt de ancho y 5 mt de largo ¿ cual sra su superficie a 35 ºc.? -
Una ventana de vidrio tiene una área de 1.6 m2 a 17°C ¿a qué temperatura debe calentarse para que mida 1.6003504m2.?. β =vidrio 14.6x10 –6 [1/(°C)] ayudenme plis
-
Una tabla de área de 2m2 y 2cm de espesor se usa como una barrera entre un cuarto a 20,0°C y una región a 50,0°C. Calcular el número de clavos de acero de 2cm de longitud y 4 mm de diámetro que se deben clavar sobre la tabla para que el flujo de calor a través de la tabla se duplique
NECESITOAYUDA
61 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar