Ecuación de la Circunferencia con Centro en el Origen
Bienvenidos de nuevo a Fisimat. En el vasto universo de la Geometría Analítica, pocas figuras son tan elegantes y fundamentales como la circunferencia. Hoy nos centraremos en su caso más puro y sencillo: la Ecuación de la Circunferencia con Centro en el Origen.
Si estás buscando cómo pasar de una fórmula a una gráfica, o tienes ejercicios de tarea que no sabes cómo atacar, has llegado al lugar indicado. Vamos a desglosar la teoría y a resolver 10 ejercicios paso a paso.
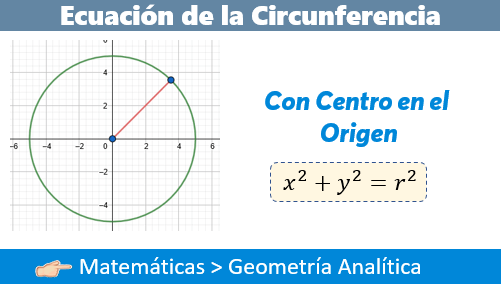
Definición de la Circunferencia
Antes de ver números y letras, entendamos qué estamos calculando. No es solo un círculo dibujado; es un conjunto de puntos con una regla estricta.
Definición Geométrica
La circunferencia es el lugar geométrico de un punto que se mueve en el plano de tal manera que su distancia a un punto fijo (llamado centro) se mantiene siempre constante. A esa distancia constante la llamamos radio (r).
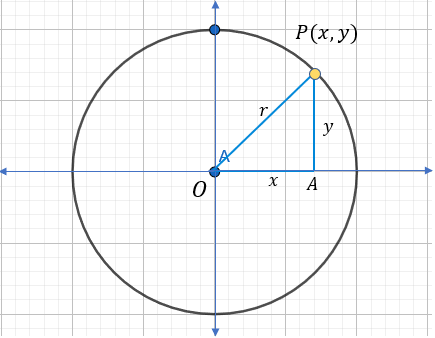
Visualmente, esto se ve así:
Tipos de Ecuaciones de la Circunferencia
Dependiendo de dónde esté ubicado el centro de la circunferencia, la fórmula cambia ligeramente de "disfraz". Es vital que sepas distinguirlas:
1. Ecuación Ordinaria (Fuera del Origen)
Se usa cuando el centro está en cualquier punto \(C(h, k)\). Su fórmula es:
\[ (x-h)^2 + (y-k)^2 = r^2 \]
2. Ecuación General
Es cuando desarrollamos los binomios y lo igualamos a cero. Tiene la forma:
\[ Ax^2 + Cy^2 + Dx + Ey + F = 0 \]
(Nota: En la circunferencia, siempre \(A = C\)).
3. Ecuación Canónica (Centro en el Origen) ⭐
Esta es la protagonista de nuestro artículo. Ocurre cuando el centro está exactamente en las coordenadas \((0,0)\). Si sustituimos \(h=0\) y \(k=0\) en la ecuación ordinaria, obtenemos la elegante forma canónica:
Fórmula Canónica
\[ x^2 + y^2 = r^2 \]
💡 ¡Conexión con Pitágoras!
Si observas bien, la ecuación \(x^2 + y^2 = r^2\) es idéntica al Teorema de Pitágoras (\(a^2 + b^2 = c^2\)). Esto es porque cualquier punto \((x,y)\) de la circunferencia forma un triángulo rectángulo con el origen, donde el radio es la hipotenusa.
Análisis del Radio
Antes de calcular, analiza el valor de \(r^2\). Matemáticamente, podemos deducir si la circunferencia existe o no:
- ✅ Si \(r^2 > 0\): La circunferencia es Real (existe y se puede dibujar).
- ❌ Si \(r^2 < 0\): La circunferencia es Imaginaria (no existe en el plano real, es imposible).
- ⚫ Si \(r^2 = 0\): La circunferencia se degenera en un solo Punto.
Ejercicios Resueltos Paso a Paso
Vamos a aplicar la fórmula canónica \(x^2 + y^2 = r^2\) en diferentes situaciones. Desde lo más básico hasta problemas de examen.
Ejemplo 1: Dado el Radio, hallar la Ecuación
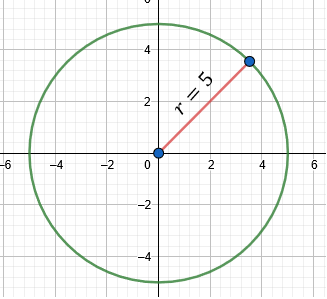
Determinar la ecuación de la circunferencia con centro en el origen cartesiano y radio \(r = 5\).
Solución:
Este es el caso más directo. Solo necesitamos sustituir \(r\) en la fórmula.
\[ x^2 + y^2 = r^2 \]
Sustituimos \(r=5\):
\[ x^2 + y^2 = (5)^2 \]
Resultado:
\[ x^2 + y^2 = 25 \]
Ejemplo 2: Convertir a Forma General
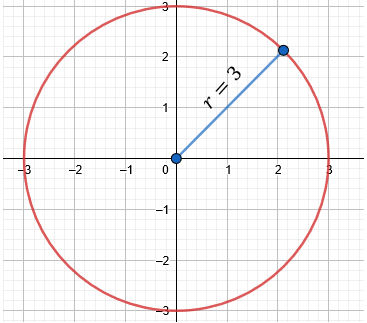
Una circunferencia tiene su centro en el origen y su radio es de 3 unidades. ¿Cuál es su ecuación en forma general?
Solución:
Primero obtenemos la forma canónica:
\[ x^2 + y^2 = 3^2 \]
\[ x^2 + y^2 = 9 \]
Para llegar a la Forma General, la regla de oro es: Todo debe estar igualado a cero. Así que pasamos el 9 al lado izquierdo restando.
Resultado:
\[ x^2 + y^2 - 9 = 0 \]
Ejemplo 3: Radio Fraccionario
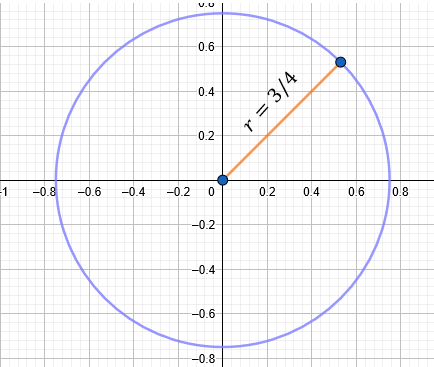
Determinar la ecuación de la circunferencia con centro en el origen y radio \(r = 3/4\).
Solución:
No te asustes con las fracciones. Aplicamos la misma lógica, recordando las leyes de los exponentes para elevar una fracción.
\[ x^2 + y^2 = \left( \frac{3}{4} \right)^2 \]
Elevamos numerador y denominador por separado (\(3^2=9\) y \(4^2=16\)):
Resultado:
\[ x^2 + y^2 = \frac{9}{16} \]
Ejemplo 4: Hallar la ecuación dado un punto P(x,y)
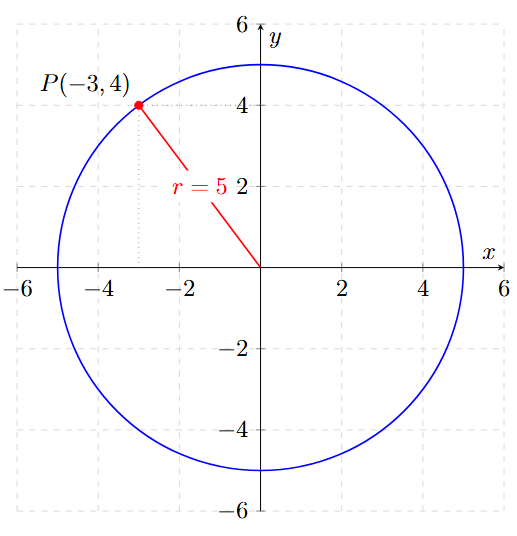
Hallar la ecuación de la circunferencia con centro en el origen que pasa por el punto \(P(-3, 4)\).
Solución:
En este caso no nos dan el radio, pero nos dan una pista: un punto \(x, y\). Usamos la ecuación para despejar \(r^2\).
\[ x^2 + y^2 = r^2 \]
Sustituimos \(x=-3\) y \(y=4\):
\[ (-3)^2 + (4)^2 = r^2 \]
\[ 9 + 16 = r^2 \]
\[ 25 = r^2 \]
Como ya sabemos que \(r^2 = 25\), ya podemos escribir la ecuación completa.
Resultado:
\[ x^2 + y^2 = 25 \]
(Nota: El radio es \(\sqrt{25} = 5\)).
Ejemplo 5: Análisis Inverso (De Ecuación a Radio)
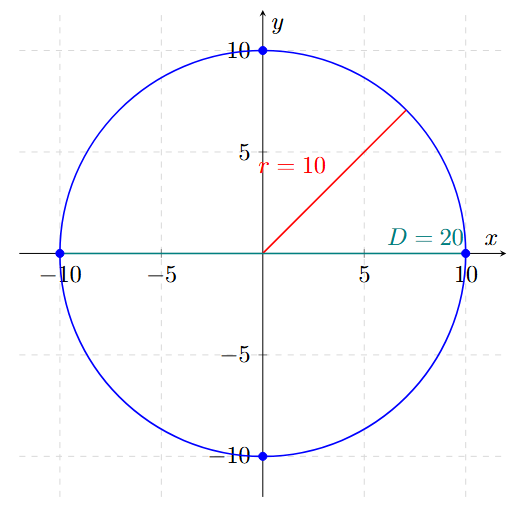
Dada la ecuación \(x^2 + y^2 = 100\), indicar cuál es el radio y el diámetro de la circunferencia.
Solución:
Comparamos la ecuación dada con la fórmula base:
- Base: \(x^2 + y^2 = r^2\)
- Dada: \(x^2 + y^2 = 100\)
Esto implica que \(r^2 = 100\). Para obtener el radio, sacamos la raíz cuadrada:
\[ r = \sqrt{100} = 10 \]
Y sabemos que el diámetro es dos veces el radio (\(D = 2r\)):
\[ D = 2(10) = 20 \]
Resultado: Radio = 10u, Diámetro = 20u.
Ejemplo 6: Hallar la ecuación dado el Área del Círculo
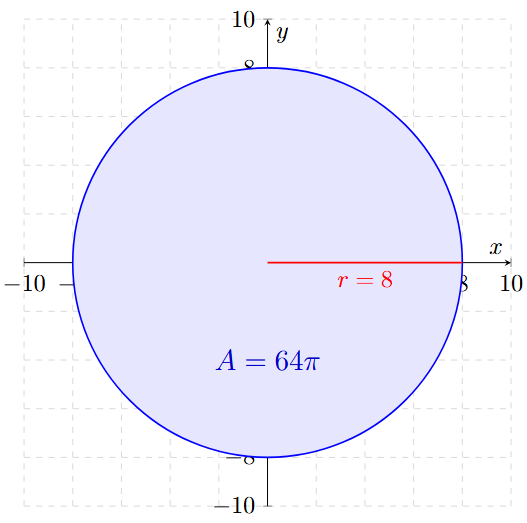
Se sabe que el área de un círculo con centro en el origen es de \(A = 64\pi \text{ u}^2\). Determinar su ecuación en forma canónica.
Solución:
A veces el dato del radio no es directo, sino que está "escondido" en el área. Recordamos la fórmula del área de un círculo:
\[ A = \pi \cdot r^2 \]
El problema nos dice que \(A = 64\pi\). Igualamos ambas expresiones:
\[ \pi \cdot r^2 = 64\pi \]
Podemos cancelar \(\pi\) en ambos lados de la ecuación:
\[ r^2 = 64 \]
¡Atención! Para la ecuación de la circunferencia no necesitamos calcular la raíz cuadrada para hallar \(r\) y luego volver a elevarlo al cuadrado. La fórmula canónica nos pide directamente \(r^2\).
\[ x^2 + y^2 = r^2 \]
Sustituyendo el valor que acabamos de encontrar:
Resultado:
\[ x^2 + y^2 = 64 \]
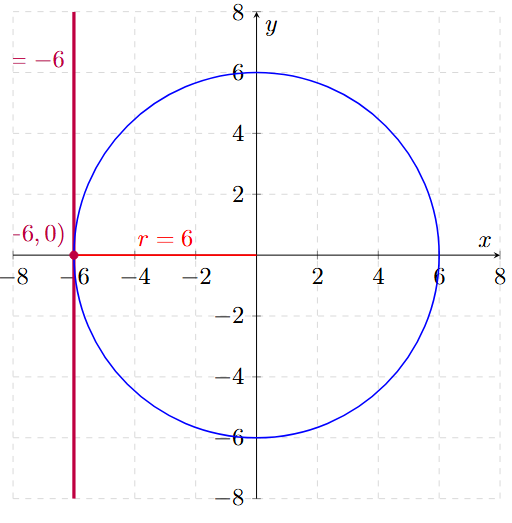
Ejemplo 7: Circunferencia Tangente a una Recta
Hallar la ecuación de la circunferencia con centro en el origen que es tangente a la recta vertical \(x = -6\).
Solución:
Este problema requiere un poco de imaginación visual (o hacer un pequeño bosquejo).
1. El centro está en \((0,0)\).
2. La recta \(x = -6\) es una línea vertical que pasa por el -6 del eje X.
La palabra "tangente" significa que la circunferencia "toca" a la recta en un solo punto sin cortarla. Por lo tanto, la distancia desde el centro \((0,0)\) hasta la recta \(x = -6\) es exactamente el valor del radio.
La distancia de 0 a -6 es 6 unidades (recordemos que las distancias siempre son positivas).
\[ r = 6 \]
Ahora aplicamos la fórmula ordinaria elevando el radio al cuadrado:
\[ x^2 + y^2 = (6)^2 \]
Resultado:
\[ x^2 + y^2 = 36 \]
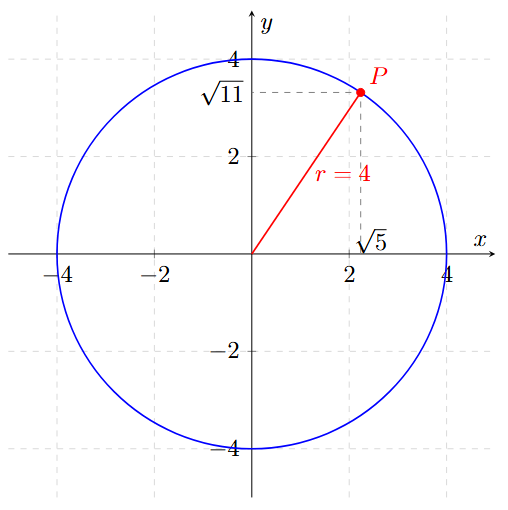
Ejemplo 8: Coordenadas con Raíces (Radicales)
Una circunferencia con centro en el origen pasa por el punto \(P(\sqrt{5}, \sqrt{11})\). Encuentra su ecuación.
Solución:
Muchos estudiantes se asustan al ver raíces cuadradas, pero en la geometría analítica suelen ser nuestros aliados porque se simplifican fácil.
Usamos la relación fundamental:
\[ r^2 = x^2 + y^2 \]
Sustituimos las coordenadas del punto \(P\):
\[ r^2 = (\sqrt{5})^2 + (\sqrt{11})^2 \]
Recordamos que una raíz cuadrada elevada al cuadrado se elimina:
\[ r^2 = 5 + 11 \]
\[ r^2 = 16 \]
Ya tenemos el valor de \(r^2\), así que simplemente escribimos la ecuación final.
Resultado:
\[ x^2 + y^2 = 16 \]
Ejercicios Propuestos de Circunferencia en el Origen
¿Listo para poner a prueba lo aprendido? Resuelve los siguientes problemas. Haz clic en la barra para ver si tu respuesta es correcta.
Problema Propuesto 1
Escribe la ecuación de una circunferencia con centro en el origen y radio \(r = 7\).
Ver Solución
Sustituimos \(7\) en \(r\).
\(x^2 + y^2 = 7^2\)
Resultado: \(x^2 + y^2 = 49\)
Problema Propuesto 2 (Con Raíz)
Determina la ecuación si el radio es \(r = \sqrt{5}\).
Ver Solución
Al elevar una raíz al cuadrado, se cancelan.
\(x^2 + y^2 = (\sqrt{5})^2\)
Resultado: \(x^2 + y^2 = 5\)
Problema Propuesto 3 (Pasa por un punto)
Encuentra la ecuación de la circunferencia que pasa por el punto \(A(2, 3)\).
Ver Solución
Calculamos \(r^2\) sustituyendo las coordenadas:
\((2)^2 + (3)^2 = r^2\)
\(4 + 9 = r^2 \Rightarrow 13 = r^2\)
Resultado: \(x^2 + y^2 = 13\)
Problema Propuesto 4 (Forma General)
Expresa en forma general la ecuación de una circunferencia con \(r = 1\).
Ver Solución
Primero canónica: \(x^2 + y^2 = 1\)
Igualamos a cero pasando el 1 restando.
Resultado: \(x^2 + y^2 - 1 = 0\)
Problema Propuesto 5 (Cálculo de Área)
Si la ecuación es \(x^2 + y^2 = 36\), calcula el área del círculo (\(A = \pi \cdot r^2\)).
Ver Solución
Sabemos que \(r^2 = 36\) (no necesitamos sacar raíz para la fórmula del área).
\(A = \pi (36)\)
Resultado: \(A = 36\pi \approx 113.09 \text{ u}^2\)
🚀 ¡Siguiente Nivel Desbloqueado!
¡Excelente! Has dominado la ecuación de la circunferencia con centro en el origen. Ya sabes interpretar radios, coordenadas y formas generales.
Pero la geometría no termina aquí. ¿Qué pasa si movemos la circunferencia fuera del origen? Descúbrelo en nuestro artículo pilar sobre Geometría Analítica o salta directamente al caso de la Ecuación Ordinaria de la Circunferencia.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
halla la suma de los términos independientes de la ecuación general de la circunferencias cuyo centro está en el eje x. Una radio igual a tres que es tangente a la recta 3x + 4y + 3 = 0
-
NICEE aqui encontre toda mi tarea jajaj muchas thankss!!
-
gracias muy buena información fácil de entender....
-
muchas gracias me ha servido mucho y me saco de un gran apuro es claro y se comprende bien ?
-
muy buenos contenidos
7 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar