Ley de Coulomb: Guía Completa + 30 Ejercicios Resueltos [PDF]
Antes de comenzar a platicar sobre la ley de Coulomb, ¿sabías que las fuerzas invisibles entre partículas cargadas son responsables de muchos de los fenómenos que observamos a diario, desde el funcionamiento de nuestros dispositivos electrónicos hasta los relámpagos en una tormenta?. La ley de Coulomb nos permite entender cómo las cargas eléctricas interactúan, ya sea atrayéndose o repeliéndose, dependiendo de su naturaleza.
En este artículo, exploraremos los principios que gobiernan estas interacciones, analizaremos casos prácticos de atracción y repulsión entre cargas, y resolveremos ejercicios que te ayudarán a dominar este fascinante tema. Este es uno de los temas que más nos han pedido en la página de física.
- ¿Quién fue Charles Coulomb?
- ✅ Ejercicios Resueltos de la Ley de Coulomb
- ⚡ Ejercicios de Ley de Coulomb con 3 Cargas (Superposición)
- 💎 Ejercicios de Ley de Coulomb con 4 Cargas (Nivel Examen)
- 🧠 Ejercicios Avanzados (Equilibrio y Dieléctricos)
- Ejercicios Para Practicar
- Resuelve el Examen de la Ley de Coulomb
- Ejercicios Resueltos en PDF de la Ley de Coulomb
- Conclusión
¿Quién fue Charles Coulomb?
Antes de hablar sobre su ley, es fundamental conocer al hombre que le dio nombre. Charles-Augustin de Coulomb fue un físico e ingeniero militar francés que sentó las bases de la electrostática.
Charles-Augustin de Coulomb
1736-1806
Físico e ingeniero francés reconocido por describir matemáticamente la ley de atracción y repulsión entre cargas eléctricas. En su honor, la unidad de carga eléctrica se denomina Culombio (C). Su trabajo fue fundamental para el desarrollo posterior de la electricidad y el magnetismo.
La Balanza de Torsión
A través de sus experimentos, postuló que cuando mayor es la distancia entre dos cuerpos cargados eléctricamente, menor será la magnitud de fuerza que haya de atracción o repulsión. Esta observación lo llevó a formular su famosa ley.
Ley de Coulomb
La magnitud de la fuerza de atracción o repulsión que experimentan dos cargas eléctricas es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia que los separa.
¿Qué es la Fuerza Eléctrica?
Es común que en los exámenes te pidan calcular la "Fuerza Eléctrica" o "Fuerza Electrostática". No te confundas: se refieren exactamente a aplicar la Ley de Coulomb. Recuerda que la fuerza es una magnitud vectorial, por lo que posee magnitud, dirección y sentido.
Este enunciado, en términos matemáticos, se expresa de la siguiente manera:
\[F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}\]
Donde:
- \(F\) = Fuerza eléctrica [Newton, N]
- \(q_{1}, q_{2}\) = Cargas eléctricas [Coulomb, C]
- \(d\) = Distancia entre las cargas [Metros, m]
- \(K\) = Constante de Coulomb
Valor de la Constante de Coulomb (K)
El valor de \(K\) es una constante de proporcionalidad que depende del medio en el que se encuentren las cargas. Para el vacío (o el aire, de forma aproximada), su valor es:
\[K \approx 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2}\]
Gráficamente, podemos ver la interacción de la siguiente forma:
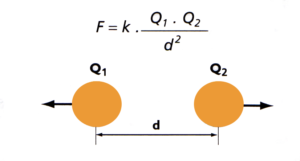
Esto quiere decir que podemos saber la fuerza de atracción o repulsión de las cargas eléctricas respecto a la distancia a la que estén separadas. Si te has dado cuenta, es similar a la ley de la gravitación universal. De todo esto, podemos deducir las reglas fundamentales:
Regla Fundamental de las Cargas
- Las cargas con el mismo signo se repelen.
- Las cargas con signos diferentes se atraen.
✅ Ejercicios Resueltos de la Ley de Coulomb
Ahora veamos los ejercicios resueltos paso a paso.
Problema 1: Fuerza de atracción
Una carga de \(3 \times 10^{-6}\) C se encuentra 2 m de una carga de \(-8 \times 10^{-6}\) C, ¿Cuál es la magnitud de la fuerza de atracción entre las cargas?
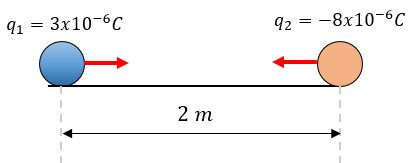
Solución: Para darle solución al ejercicio, debemos de obtener los datos para poder resolverlo de manera directa.
Datos:
- \(q_1 = 3 \times 10^{-6} \, \text{C}\)
- \(q_2 = -8 \times 10^{-6} \, \text{C}\)
- \(d = 2 \, \text{m}\)
- \(K = 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2}\)
Aplicando la fórmula de la ley de coulomb:
\[ F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}} \]
Sustituimos los valores:
\[ F=\left[ 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right] \frac{(3 \times 10^{-6} \, \text{C}) \cdot (-8 \times 10^{-6} \, \text{C})}{ (2 \, \text{m})^2 } \]
\[ F=\left[ 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right] \frac{-24 \times 10^{-12} \, \text{C}^2}{4 \, \text{m}^2} \]
Dividimos y multiplicamos:
\[ F=\left[ 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right] (-6 \times 10^{-12} \, \frac{\text{C}^2}{\text{m}^2}) \]
\[ F = -54 \times 10^{-3} \, \text{N} = -0.054 \, \text{N} \]
El signo negativo indica que la fuerza es de atracción. Como el problema nos pide la magnitud, tomamos el valor absoluto.
Resultado: \(F = 0.054 \, \text{N}\)
Problema 2: Calcular la segunda carga
Una carga de \(-5 \times 10^{-7}\) C ejerce una fuerza a otra carga de 0.237 N a una distancia de 3.5 metros, ¿cuál es el valor de la segunda carga?
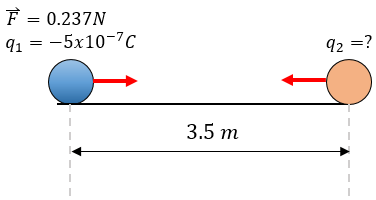
Solución: Ahora nos piden hallar el valor de la segunda carga. Debemos despejar \(q_2\) de la fórmula.
Datos:
- \(q_1 = -5 \times 10^{-7} \, \text{C}\)
- \(F = 0.237 \, \text{N}\)
- \(d = 3.5 \, \text{m}\)
- \(q_2 = ?\)
Despejando la fórmula para \(q_2\):
\[ F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}} \Rightarrow F \cdot d^2 = K \cdot q_1 \cdot q_2 \]
\[ q_2 = \frac{F \cdot d^2}{K \cdot q_1} \]
Ahora vamos a sustituir nuestros datos:
\[ q_2 = \frac{ (0.237 \, \text{N}) (3.5 \, \text{m})^2 }{ \left[ 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right] \cdot (-5 \times 10^{-7} \, \text{C}) } \]
\[ q_2 = \frac{ (0.237 \, \text{N}) (12.25 \, \text{m}^2) }{ -4500 \, \frac{\text{N·m}^2}{\text{C}} } \]
\[ q_2 = \frac{ 2.90 \, \text{N·m}^2 }{ -4500 \, \frac{\text{N·m}^2}{\text{C}} } \]
\[ q_2 = -0.000644 \, \text{C} = -6.44 \times 10^{-4} \, \text{C} \]
Resultado: \(q_2 = -6.44 \times 10^{-4} \, \text{C}\)
Problema 3: Calcular la distancia
Dos cargas con \(2.8 \times 10^{-6}\) C y \(7.5 \times 10^{-6}\) C respectivamente se atraen con una fuerza de 10 N, ¿A qué distancia se encuentran separadas?

Solución: En este caso nuestra incógnita será la distancia \(d\).
Datos:
- \(q_1 = 2.8 \times 10^{-6} \, \text{C}\)
- \(q_2 = 7.5 \times 10^{-6} \, \text{C}\)
- \(F = 10 \, \text{N}\)
- \(d = ?\)
Despejamos \(d\) de la fórmula de la ley de Coulomb:
\[ F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}} \Rightarrow F \cdot d^2 = K \cdot q_1 \cdot q_2 \]
\[ d^2 = \frac{K \cdot q_1 \cdot q_2}{F} \Rightarrow d = \sqrt{\frac{K \cdot q_1 \cdot q_2}{F}} \]
Ahora tenemos que sustituir nuestros datos:
\[ d = \sqrt{ \frac{ \left( 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right) (2.8 \times 10^{-6} \, \text{C}) (7.5 \times 10^{-6} \, \text{C}) }{ 10 \, \text{N} } } \]
\[ d = \sqrt{ \frac{ 0.189 \, \text{N·m}^2 }{ 10 \, \text{N} } } = \sqrt{ 0.0189 \, \text{m}^2 } \]
\[ d = 0.1374 \, \text{m} \]
Resultado: \(d = 0.1374 \, \text{m}\) (o 13.74 cm)
Problema 4: Repaso de cálculo de distancia
Dos cargas de \(5.0 \times 10^{-6}\) C y \(3.0 \times 10^{-6}\) C se atraen con una fuerza de \(15\) N. ¿Cuál es la distancia entre ellas?

Solución: Este problema es similar al anterior y nos ayudará a reforzar.
Datos:
- \(q_1 = 5.0 \times 10^{-6} \, \text{C}\)
- \(q_2 = 3.0 \times 10^{-6} \, \text{C}\)
- \(F = 15 \, \text{N}\)
- \(d = ?\)
Usamos la fórmula despejada para \(d\):
\[ d = \sqrt{\frac{K \cdot q_1 \cdot q_2}{F}} \]
Sustitución:
\[ d = \sqrt{ \frac{ \left( 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right) (5.0 \times 10^{-6} \, \text{C}) (3.0 \times 10^{-6} \, \text{C}) }{ 15 \, \text{N} } } \]
\[ d = \sqrt{ \frac{ 0.135 \, \text{N·m}^2 }{ 15 \, \text{N} } } = \sqrt{ 0.009 \, \text{m}^2 } \]
\[ d = 0.0949 \, \text{m} \]
Resultado: \(d = 0.0949 \, \text{m}\) (o 9.49 cm)
Problema 5: Repaso de cálculo de carga
Dos cargas eléctricas ejercen una fuerza de 7 N. Si \(q_2 = 3.5 \times 10^{-6}\) C y están separadas por 0.2 m, calcula el valor de \(q_1\).
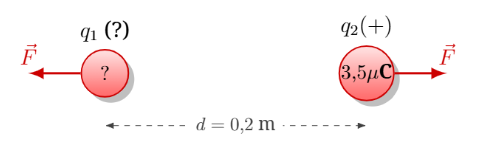
Solución:
Datos:
- \(F = 7 \, \text{N}\)
- \(q_2 = 3.5 \times 10^{-6} \, \text{C}\)
- \(d = 0.2 \, \text{m}\)
- \(q_1 = ?\)
Usamos la fórmula despejada para \(q_1\):
\[ q_1 = \frac{F \cdot d^2}{K \cdot q_2} \]
Sustitución:
\[ q_1 = \frac{ (7 \, \text{N}) (0.2 \, \text{m})^2 }{ \left( 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right) (3.5 \times 10^{-6} \, \text{C}) } \]
\[ q_1 = \frac{ (7 \, \text{N}) (0.04 \, \text{m}^2) }{ 31500 \, \frac{\text{N·m}^2}{\text{C}} } \]
\[ q_1 = \frac{ 0.28 \, \text{N·m}^2 }{ 31500 \, \frac{\text{N·m}^2}{\text{C}} } = 8.888 \times 10^{-6} \, \text{C} \]
Resultado: \(q_1 \approx 8.89 \times 10^{-6} \, \text{C}\)
Problema 6: Calcular carga desconocida
Una carga desconocida (\(q_2\)) y otra de \(8 \times 10^{-6}\) C se repelen con 10 N a 0.15 m de distancia. Determina \(q_2\).
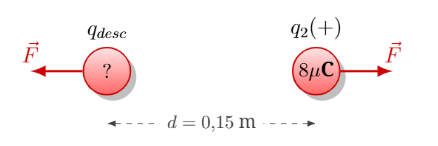
Solución:
Datos:
- \(F = 10 \, \text{N}\)
- \(q_1 = 8 \times 10^{-6} \, \text{C}\)
- \(d = 0.15 \, \text{m}\)
- \(q_2 = ?\)
Usamos la fórmula despejada para \(q_2\):
\[ q_2 = \frac{F \cdot d^2}{K \cdot q_1} \]
Sustitución:
\[ q_2 = \frac{ (10 \, \text{N}) (0.15 \, \text{m})^2 }{ \left( 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \right) (8 \times 10^{-6} \, \text{C}) } \]
\[ q_2 = \frac{ (10 \, \text{N}) (0.0225 \, \text{m}^2) }{ 72000 \, \frac{\text{N·m}^2}{\text{C}} } \]
\[ q_2 = \frac{ 0.225 \, \text{N·m}^2 }{ 72000 \, \frac{\text{N·m}^2}{\text{C}} } = 3.125 \times 10^{-6} \, \text{C} \]
Resultado: \(q_2 = 3.125 \times 10^{-6} \, \text{C}\)
Problema 7: Comprobación de la constante K
Comprueba el valor de \(K\) si dos cargas de \(2 \times 10^{-6}\) C y \(5 \times 10^{-6}\) C, separadas por 0.1 m, ejercen una fuerza de 9 N.
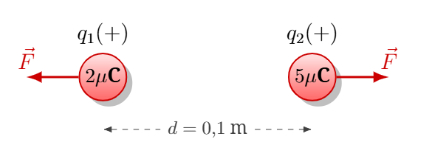
Solución:
Datos:
- \(F = 9 \, \text{N}\)
- \(q_1 = 2 \times 10^{-6} \, \text{C}\)
- \(q_2 = 5 \times 10^{-6} \, \text{C}\)
- \(d = 0.1 \, \text{m}\)
- \(K = ?\)
Despeje de \(K\):
\[ F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}} \Rightarrow K = \frac{F \cdot d^2}{q_1 \cdot q_2} \]
Sustitución:
\[ K = \frac{ (9 \, \text{N}) (0.1 \, \text{m})^2 }{ (2 \times 10^{-6} \, \text{C}) (5 \times 10^{-6} \, \text{C}) } \]
\[ K = \frac{ (9 \, \text{N}) (0.01 \, \text{m}^2) }{ 10 \times 10^{-12} \, \text{C}^2 } \]
\[ K = \frac{ 0.09 \, \text{N·m}^2 }{ 1 \times 10^{-11} \, \text{C}^2 } = 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2} \]
Resultado: Se comprueba correctamente el valor de \(K = 9 \times 10^9 \, \frac{\text{N·m}^2}{\text{C}^2}\).
⚡ Ejercicios de Ley de Coulomb con 3 Cargas (Superposición)
Cuando tenemos tres o más cargas, entramos en el terreno de los Vectores. Aquí aplicamos el Principio de Superposición: la fuerza neta sobre una carga es la suma vectorial de las fuerzas individuales que ejercen las demás cargas.
Ejemplo 8: Sistema Lineal de 3 Cargas
Tres cargas están alineadas sobre el eje X. \(q_1 = 4 \mu C\) en el origen, \(q_2 = -2 \mu C\) a 10 cm a la derecha de \(q_1\), y \(q_3 = 5 \mu C\) a 15 cm a la derecha de \(q_2\). Calcula la fuerza resultante sobre la carga central (\(q_2\)).

Solución:
Analizamos las fuerzas sobre \(q_2\) (la carga del medio):
1. \(q_1\) (positiva) atrae a \(q_2\) (negativa) hacia la izquierda (Fuerza negativa).
2. \(q_3\) (positiva) atrae a \(q_2\) (negativa) hacia la derecha (Fuerza positiva).
Datos:
- \(q_1 = 4 \times 10^{-6} \text{ C}\)
- \(q_2 = 2 \times 10^{-6} \text{ C}\) (usamos valor absoluto para la fórmula)
- \(q_3 = 5 \times 10^{-6} \text{ C}\)
- \(r_{12} = 0.1 \text{ m}\)
- \(r_{23} = 0.15 \text{ m}\)
Calculamos las magnitudes:
\[ F_{12} = K \frac{q_1 q_2}{r_{12}^2} = (9 \times 10^9) \frac{(4 \times 10^{-6})(2 \times 10^{-6})}{(0.1)^2} = 7.2 \text{ N} \]
\[ F_{32} = K \frac{q_3 q_2}{r_{23}^2} = (9 \times 10^9) \frac{(5 \times 10^{-6})(2 \times 10^{-6})}{(0.15)^2} = 4 \text{ N} \]
Suma Vectorial:
Tomando la derecha como positivo:
\[ F_R = F_{32} - F_{12} = 4 \text{ N} - 7.2 \text{ N} = -3.2 \text{ N} \]
Resultado: La fuerza resultante es de 3.2 N hacia la izquierda.
Ejemplo 9: Sistema Triangular (2D)
Tres cargas forman un triángulo rectángulo. \(q_1 = -6 \mu C\) está en el origen (0,0), \(q_2 = 4 \mu C\) está en el eje Y a 0.3 m (0, 0.3) y \(q_3 = 4 \mu C\) está en el eje X a 0.4 m (0.4, 0). Calcule la fuerza resultante sobre la carga en el origen (\(q_1\)).
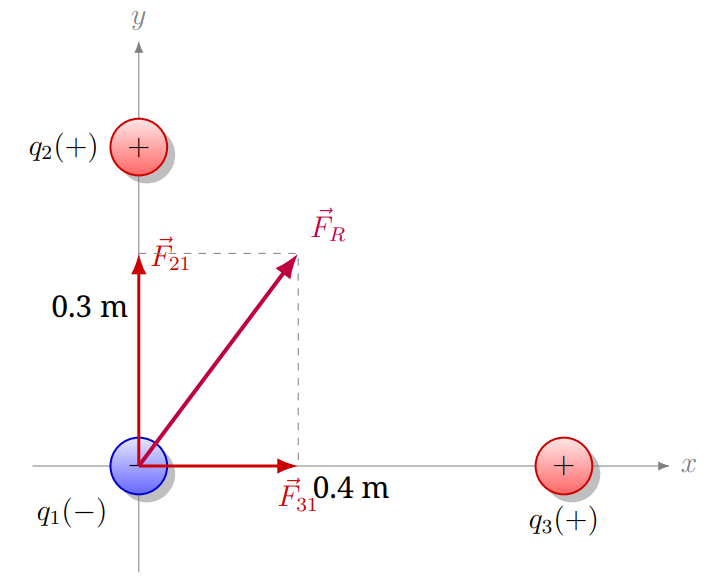
Solución:
Como \(q_1\) es negativa y las otras son positivas, ambas la atraen.
1. \(q_2\) atrae a \(q_1\) hacia arriba (Eje +Y).
2. \(q_3\) atrae a \(q_1\) hacia la derecha (Eje +X).
Cálculo de Fuerzas:
\[ F_{21} = (9 \times 10^9) \frac{(4 \times 10^{-6})(6 \times 10^{-6})}{(0.3)^2} = 2.4 \text{ N} \text{ (Hacia arriba)} \]
\[ F_{31} = (9 \times 10^9) \frac{(4 \times 10^{-6})(6 \times 10^{-6})}{(0.4)^2} = 1.35 \text{ N} \text{ (Hacia la derecha)} \]
Fuerza Resultante (Teorema de Pitágoras):
Al ser fuerzas perpendiculares:
\[ F_R = \sqrt{(F_{31})^2 + (F_{21})^2} = \sqrt{(1.35)^2 + (2.4)^2} \]
\[ F_R = \sqrt{1.8225 + 5.76} = \sqrt{7.5825} = 2.75 \text{ N} \]
Resultado: \(F_R = 2.75 \text{ N}\)
💎 Ejercicios de Ley de Coulomb con 4 Cargas (Nivel Examen)
Aquí es donde la mayoría se confunde. Para sistemas de 4 cargas, el orden es vital. Vamos a ver un caso lineal y uno geométrico (cuadrado).
Ejemplo 10: Cuatro Cargas en Línea
Cuatro cargas puntuales idénticas de \(q = 2 \mu C\) están situadas en el eje X en las posiciones \(x=0, x=2, x=4, x=6\) cm respectivamente. Calcule la fuerza resultante sobre la carga que está en \(x=6\) cm (la última a la derecha).
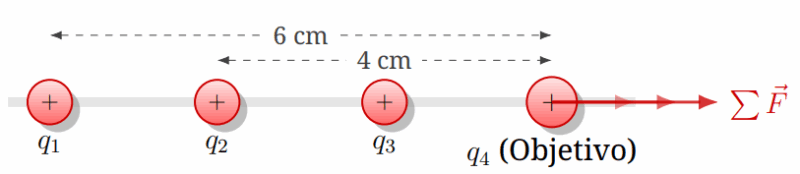
Solución:
Llamemos a las cargas 1, 2, 3 y 4 (de izquierda a derecha). Queremos la fuerza sobre la carga 4.
Como todas son positivas, todas repelen a la carga 4 hacia la derecha (dirección positiva).
Distancias respecto a la carga 4:
- \(r_{34} = 2 \text{ cm} = 0.02 \text{ m}\)
- \(r_{24} = 4 \text{ cm} = 0.04 \text{ m}\)
- \(r_{14} = 6 \text{ cm} = 0.06 \text{ m}\)
Calculamos cada repulsión individual:
\[ F_{34} = K \frac{q^2}{(0.02)^2} = (9\times10^9)\frac{(2\times10^{-6})^2}{0.0004} = 90 \text{ N} \]
\[ F_{24} = K \frac{q^2}{(0.04)^2} = (9\times10^9)\frac{(2\times10^{-6})^2}{0.0016} = 22.5 \text{ N} \]
\[ F_{14} = K \frac{q^2}{(0.06)^2} = (9\times10^9)\frac{(2\times10^{-6})^2}{0.0036} = 10 \text{ N} \]
Fuerza Total:
\[ F_T = 90 + 22.5 + 10 = 122.5 \text{ N} \]
Resultado: \(122.5 \text{ N}\) hacia la derecha.
Ejemplo 11: Cuadrado de Cargas (Reto Vectorial)
Cuatro cargas positivas de magnitud \(q = 10 \mu C\) se colocan en los vértices de un cuadrado de lado \(L = 1 \text{ m}\). Calcule la fuerza resultante sobre la carga ubicada en el vértice superior derecho.
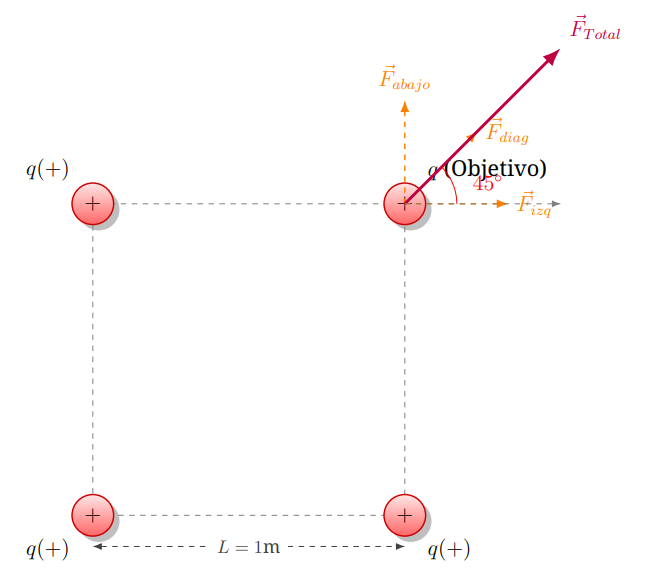
Solución:
Analizamos la carga superior derecha. Recibe 3 fuerzas de repulsión:
1. \(F_1\): De la carga a su izquierda (Horizontal).
2. \(F_2\): De la carga abajo (Vertical).
3. \(F_3\): De la carga en la esquina opuesta (Diagonal a 45°).
Calculamos magnitudes:
\[ F_1 = K \frac{q^2}{L^2} = (9\times10^9)\frac{(10^{-5})^2}{1^2} = 0.9 \text{ N} \]
\(F_2\) es idéntica por simetría: \(F_2 = 0.9 \text{ N}\).
Para \(F_3\), la distancia es la diagonal (\(d = \sqrt{1^2+1^2} = \sqrt{2}\)):
\[ F_3 = K \frac{q^2}{(\sqrt{2})^2} = (9\times10^9)\frac{10^{-10}}{2} = 0.45 \text{ N} \]
Descomposición de Vectores:
La fuerza \(F_3\) está a 45°, así que tiene componentes en X y Y:
\[ F_{3x} = 0.45 \cos(45^\circ) = 0.318 \text{ N} \]
\[ F_{3y} = 0.45 \sin(45^\circ) = 0.318 \text{ N} \]
Sumatoria Total:
\[ F_x = F_1 + F_{3x} = 0.9 + 0.318 = 1.218 \text{ N} \]
\[ F_y = F_2 + F_{3y} = 0.9 + 0.318 = 1.218 \text{ N} \]
Fuerza Resultante:
\[ F_R = \sqrt{(1.218)^2 + (1.218)^2} = 1.72 \text{ N} \]
Resultado: \(1.72 \text{ N}\) a 45°.
🧠 Ejercicios Avanzados (Equilibrio y Dieléctricos)
Para cerrar con broche de oro, veamos casos especiales: cuando las cargas no están en el vacío o cuando buscamos el punto de equilibrio.
Ejemplo 12: Punto de Equilibrio (Fuerza Neta Cero)
Dos cargas \(q_1 = 4 \mu C\) y \(q_2 = 16 \mu C\) están separadas por una distancia de 90 cm. ¿A qué distancia de la carga \(q_1\) se debe colocar una tercera carga \(q_3\) para que la fuerza eléctrica neta sobre ella sea cero?
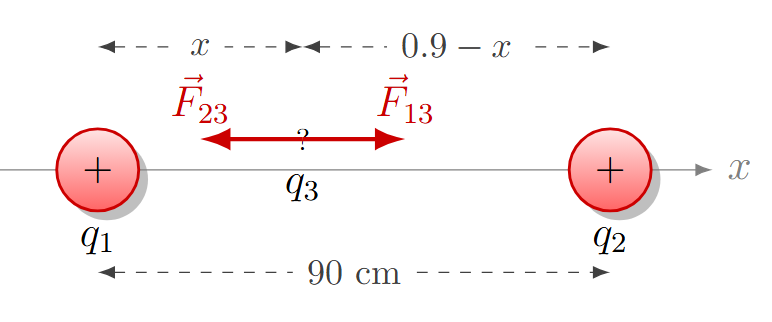
Solución:
Para que la fuerza sea cero, la fuerza que \(q_1\) ejerce sobre \(q_3\) debe ser igual y opuesta a la que \(q_2\) ejerce sobre \(q_3\).
\[ F_{13} = F_{23} \]
\[ K \frac{q_1 q_3}{x^2} = K \frac{q_2 q_3}{(d-x)^2} \]
Cancelamos \(K\) y \(q_3\) (no importa el valor de la tercera carga):
\[ \frac{q_1}{x^2} = \frac{q_2}{(0.9 - x)^2} \]
Sustituimos valores (\(q_1=4, q_2=16\)):
\[ \frac{4}{x^2} = \frac{16}{(0.9 - x)^2} \]
Sacamos raíz cuadrada a ambos lados para facilitar el despeje:
\[ \frac{2}{x} = \frac{4}{0.9 - x} \]
Multiplicamos cruzado:
\[ 2(0.9 - x) = 4x \]
\[ 1.8 - 2x = 4x \Rightarrow 1.8 = 6x \]
\[ x = \frac{1.8}{6} = 0.3 \text{ m} \]
Resultado: Se debe colocar a 30 cm de la carga \(q_1\).
Ejemplo 13: Cargas en Aceite (Permitividad)
Dos cargas se repelen con una fuerza de 20 N en el vacío. Si las mismas cargas se sumergen en aceite (cuya permitividad relativa es \(\varepsilon_r = 2.5\)) a la misma distancia, ¿cuál será la nueva fuerza?

Solución:
La Ley de Coulomb cambia según el medio. La fuerza en un medio se reduce según la constante dieléctrica.
\[ F_{\text{medio}} = \frac{F_{\text{vacío}}}{\varepsilon_r} \]
\[ F_{\text{aceite}} = \frac{20 \text{ N}}{2.5} \]
\[ F_{\text{aceite}} = 8 \text{ N} \]
Resultado: La fuerza se reduce a 8 N.
Ejemplo 14: Levitación de Cargas (Fuerza vs Gravedad)
Una esfera de 0.5 kg con carga eléctrica desconocida \(q\) está suspendida en el aire, justo encima de otra esfera fija con carga \(Q = 50 \mu C\). Si la distancia entre ellas es de 10 cm, ¿cuánto debe valer \(q\) para que la esfera flote en equilibrio?
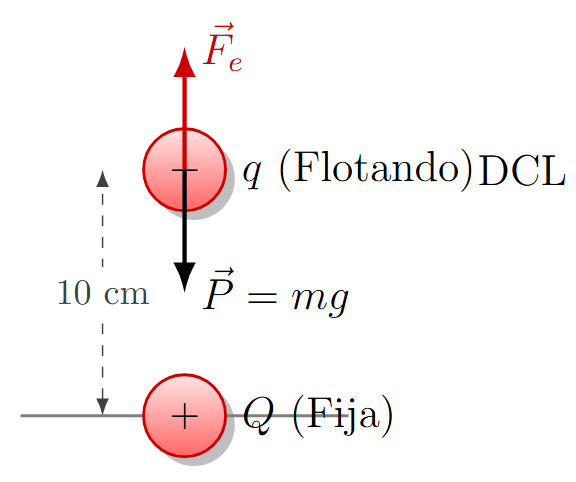
Solución:
Para que "flote", la Fuerza Eléctrica de repulsión (hacia arriba) debe anular al Peso (hacia abajo).
\[ F_e = P \Rightarrow F_e = m \cdot g \]
Calculamos el peso:
\[ P = (0.5 \text{ kg})(9.8 \text{ m/s}^2) = 4.9 \text{ N} \]
Igualamos a la fórmula de Coulomb y despejamos \(q\):
\[ K \frac{Q \cdot q}{d^2} = 4.9 \]
\[ q = \frac{4.9 \cdot d^2}{K \cdot Q} \]
\[ q = \frac{4.9 \cdot (0.1)^2}{(9\times10^9)(50\times10^{-6})} \]
\[ q = \frac{0.049}{450,000} = 1.08 \times 10^{-7} \text{ C} \]
Resultado: La carga debe ser \(q = 108 \text{ nC}\) (nanoCoulombs).
Ejemplo 15: Triángulo Equilátero (3 Cargas Idénticas)
Tres cargas de \(+2 \mu C\) se colocan en los vértices de un triángulo equilátero de lado \(L=10 \text{ cm}\). Calcule la magnitud de la fuerza resultante sobre la carga del vértice superior.

Solución:
Por simetría, las componentes horizontales (X) se cancelan y las verticales (Y) se suman.
Distancia \(r = 0.1 \text{ m}\). Ángulo de las fuerzas con la vertical = 30° (o 60° con la horizontal).
Magnitud de una fuerza individual \(F\):
\[ F = K \frac{q^2}{r^2} = (9\times10^9) \frac{(2\times10^{-6})^2}{(0.1)^2} = 3.6 \text{ N} \]
Como son dos fuerzas empujando hacia arriba en ángulo:
\[ F_R = 2 \cdot F \cdot \cos(30^\circ) \]
\[ F_R = 2 \cdot (3.6) \cdot (0.866) \]
\[ F_R = 6.235 \text{ N} \]
Resultado: 6.235 N hacia arriba.
Ejercicios Para Practicar
Genial, ahora es momento de practicar y analizar si realmente hemos comprendido los problemas resueltos.
Problema de Práctica 16
Calcular la magnitud de la fuerza eléctrica entre dos cargas cuyos valores son: \(q_1\) = 3.5 milicoulombs y \(q_2\) = 6 milicoulombs, al estar separadas en el vacío por una distancia de 40 cm.
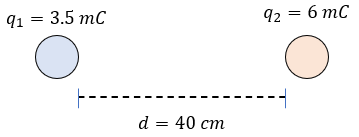
Problema de Práctica 17
Determinar la fuerza eléctrica entre dos cargas cuyos valores son \(q_1\) = -3 microcoulombs y \(q_2\) = 5.5 microcoulombs, al estar separadas en el vacío por una distancia de 70 cm.
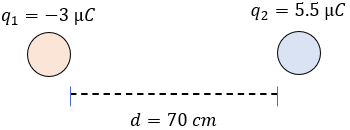
Problema de Práctica 18
Una carga eléctrica de 3 microcoulombs se encuentran en el aire a 35 cm de otra carga. La magnitud de la fuerza con la cual se rechazan es de \(6 \times 10^{-1}\) N. ¿Cuánto vale la carga desconocida?
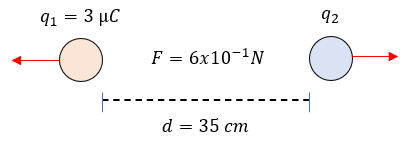
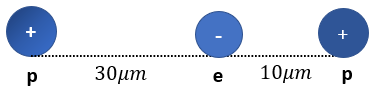
Problema de Práctica 19: Fuerzas Netas
Dos protones están a cada lado de un electrón como se muestra en la imagen, considerando que el electrón está a 30 µm del protón a su izquierda y a 10 µm del protón a su derecha. ¿Cuál es la magnitud y la dirección de la fuerza eléctrica neta que actúa sobre el electrón?
Resuelve el Examen de la Ley de Coulomb
Llegó el momento de que pongas a pruebas tus conocimientos de la Ley de Coulomb. ¿Podrás lograr obtener todas buenas? 🚀💛
Cargando examen...
Ejercicios Resueltos en PDF de la Ley de Coulomb
Descarga la Guía PDF Gratuita
He preparado esta guía completa con todos los ejercicios resueltos paso a paso. Es perfecta para que la guardes, la imprimas y la uses para estudiar en cualquier lugar, incluso sin conexión a internet. ¡Ideal para repasar antes de tu examen!
🔒 Descarga segura desde Google Drive • 100% Gratuito
Conclusión
Puntos Clave para Recordar
La Ecuación de Coulomb solamente es válida cuando las cargas se encuentran en el vacío, o hay una aproximación muy cercana al aire, puesto que la permitividad relativa es próxima al vacío.
Como te podrás dar cuenta, no es difícil, simplemente debemos establecer nuestros datos y resolver. Si tienes problemas de despeje, que es lo más común, hemos ya publicado en el blog un artículo sobre cómo despejar fórmulas. Así no tendrás ese tipo de situaciones incómodas.
Ahora, la Ley de Coulomb no solo se define para dos cargas. Cuando hay más de dos, el problema se vuelve más complejo y subimos un poco el nivel. A dicho tema se le conoce como el principio de superposición, ¡del cual ya tenemos ejemplos resueltos!
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Excelente los ejercicios
★★★★★
-
dos cargas q1=5 uC y q2 =-3uC estan separadas por una distancia de 0.4m0.4, m0.4m. utiliza la formula de la ley de coulomb para calcular la magnitud de la fuerza q actúa entre ellas ¿es una fuerza de atracción o repulsión ?
-
según yo es atracción
★★★★★
-
-
Cuál debe ser la distancia de separación entre dos cargas de 4 * 10^- 5 C cada una para la fuerza de repulsión entre ellas tenga un módulo de 160N
-
emm..por que a mi me da 2.45x10-17 en la actividad 6? 🙁
-
dos cargas puntuales se encuentran cargadas con 3c y -4c. si se acercan a una distancia de 1cm ¿ cual es la fuerza de atraccion entre ellas?
715 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar